深入剖析堆原理与堆排序

堆的介绍

• 完全二叉树：完全二叉树是满二叉树去除最后N个节点之后得到的树（$N\ge 0,N\in N^{\ast }$）
• 大根堆：节点的父亲节点比自身节点大，比如根节点的值为$8$，比其子节点 $7$, $6$大，其余的类似。

• 小根堆：节点的父亲节点比自身节点小，比如根节点的值为$1$，比其子节点$2$, $3$的值要小，其余的也类似。

堆的实现

如何存储一个堆

堆的存储是使用数组实现的，下标从0开始从左至右从上到下，依次递增，例如上述的小根堆存储在数组中就是

[1, 2, 3, 4, 5, 6, 7]

对应的下标为 $0,1,2,3,4,5,6$

如何将一个数组变成一个堆

从最后一个有孩子节点 （节点下标为$M$）的元素开始，先将以该元素为根节点的子树变成一个堆，然后下标减 $1$，再将下标为$M-1$的节点所对应的子树变成堆，依次递减进行，直到根节点。示例如下（以小根堆为例）：

• 找到第一个有孩子节点的，由上图容易知道，第一个有孩子节点的值为$5$，其下标为$3$，它对应的子树为：

  

  如果需要将上面的子树变成一颗小根堆，只需要将$5$和$1$对应节点互换位置即可（不能和$2$换，如果和$2$换 $2>1$不符合小根堆的性质），换完之后的结果为：

  

• 然后将下标减$1$，即为$2$，对应的元素为$6$，现在也需要将其对应的子树变成一颗小根堆，即需要将$6$和$2$互换，互换之后的结果为：

  

• 继续将下标减$1$，然后进行相同的操作，很容易知道将$7$和$1$互换位置，互换之后的结果为：

  

从上面的图可以知道，当$1$和$7$互换之后，子树$[7,2,5]$不是一颗小根堆了，那怎么办？再将子树$[7,2,5]$变成小根堆即可，所以再进行一次小根堆操作即可，将$7$, $2$进行互换即可，交换之后的结果为：

在上述的树中，交换过程已经完成了，但是如果节点的数目非常大，或者说下面的子树可能又出现了不符合小根堆的情况怎么办？那就一直循环走下去，直到没有孩子节点或者已经满足小根堆的性质。我们将上述操作定义为下沉(down)操作

• 最后再对节点$8$进行相关操作，得到的结果如下：

  

• 再对子树进行堆化$(heapify)$操作:

  

• 在进行堆化，得到最终结果

  

以上就是将一个完全二叉树变成一颗小根堆的过程，大根堆的过程非常类似，即将较大的数作为父亲节点即可，就不在进行陈述~~~

代码实现

首先我们清楚堆的存储数据结构是数组，那么就有对应的下标，那么父亲节点和孩子节点的位置对应关系是什么呢？

如果父亲节点的下标为$i$那么它对应的做孩子的下标为$2\ast i+1$对应右孩子的下标为$2\ast i+2$，如果孩子节点的下标为$i$，则对应的父亲节点的下标为$\lfloor \frac{i-1}{2}\rfloor$，可以参考下图进行计算。

根据上面的分析我们可以知道，如果想把一个数组变成一个堆，那么需要从最后一个有孩子的节点开始进行下沉操作，直到根节点。

下沉操作的具体步骤，如果是小根堆，就将当前节点的值和左右孩子节点进行比较，如果当前节点$V$比左右孩子节点都小的话则停止，或者当前节点没有孩子节点也停止，如果子节点的值比当前节点小，则需要选取子节点中较小的值，然后和当前节点互换，然后在置换后对$V$重新进行上述操作。如果是大根堆则选取孩子节点中较大的值。具体代码如下：

#include 
#include 
#include 
#include 
 
#define True 1
#define False 0
#define NUM 9
#define MAX_VALUE 100
 
void swap(int * array, int idx1, int idx2) {
    /*交换数组的两个元素*/
    int t = array[idx1];
    array[idx1] = array[idx2];
    array[idx2] = t;
}
 
void down(int * array, int length, int start, int big=False) {
    /* array 是堆数组，length 为数组的长度，start 是当前需要下沉的元素的下标，big 表示是否为大根堆 */
    while(start < length) {
        int left_child = 2 * start + 1;
        int right_child = 2 * start + 2;
        int idx = left_child;
        if (left_child > length - 1)
            /* 如果做孩子对应的下标超出数组元素个数则需要跳出循环 */
            break;
        if(right_child < length) {
            if (!big) {
                if(array[right_child] < array[left_child])
                    idx = right_child;
            } else {
                if(array[right_child] > array[left_child])
                    idx = right_child;
            }
        }
        if(!big) {
            if(array[start] > array[idx]){
                swap(array, idx, start);
                start = idx;
            } else{
                break;
            }
        } else {
            if(array[start] < array[idx]){
                swap(array, idx, start);
                start = idx;
            } else{
                break;
            }
        }
    }
}
 
/* 定义对整个数组的堆化过程 */
void heapify(int * array, int length, int start=-2, int big=True) {
	/* start 的默认值为 -2 表示从最后一个有孩子节点的元素开始 */
    if(start == -1) 
        /* 最后一个元素的下标为0 再减1则为-1 在这里设置递归出口*/
        return;
    if (start == -2) {
        start = (length - 2) / 2;
    }
    down(array, length, start, big);
    /* 当前元素进行下沉操作之后 再对他的上一个元素进行 下沉操作*/
    heapify(array, length, start - 1, big);
}
 
int main() {
    int data[NUM] = {0, 1, 2, 3, 4, 5, 6, 7, 8};
    heapify(data, NUM);
    for(int i=0; i < NUM; i++) {
        printf("%d ", data[i]);
    }
    return 0;
}
/* output : 8 7 6 3 4 5 2 1 0 */

堆的应用

堆排序

对于数组array = {0, 7, 3, 5, 1, 6, 2, 4, 8}对应的堆如下图所示，如果想使用堆排序，首先需要将数组变成一个堆，使用上面的heapify函数即可。

先将数组变成大根堆，变换过程如下图所示：

最终得到的大根堆如图7所示。得到一个大根堆之后怎么排序呢？我们知道对于一个大根堆来说，根节点的孩子节点都比他小，所以根节点一定是堆中值最大的元素，现在将根节点和最后一个节点互换位置，置换后的结果如下图所示：

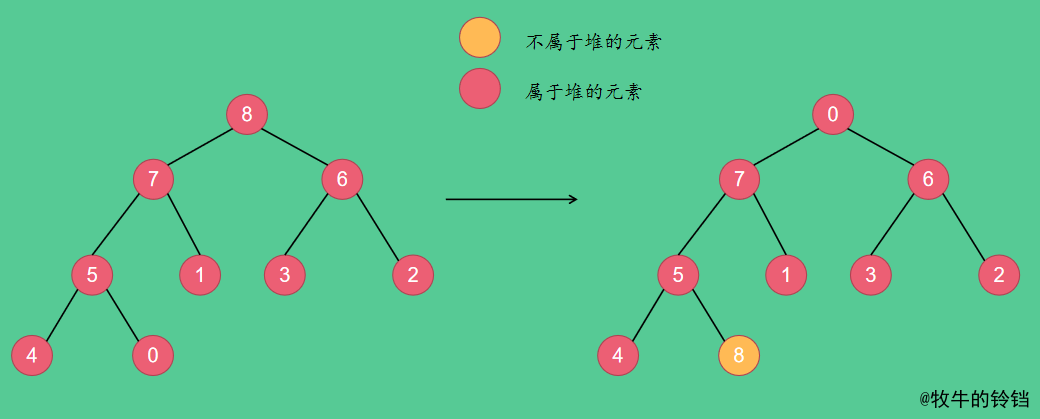
现在已经将数组中最大的元素放到数组的最后一个元素了，现在我们将最后一个元素从堆中剔除，对于这个操作我们只需要将堆的长度减1，对于存储在数组中的数据不需要改动，即现在堆中的元素只有{0, 7, 6, 5, 1, 3, 2, 4}，但是实际在数组中的元素仍然为{0, 7, 6, 5, 1, 3, 2, 4, 8}。现在对元素0进行下沉操作。操作过程如下图所示：

最终会得到结果V，因为元素8已经不在堆中了，因此不会和8置换，这样堆中最大的元素就在数组最后一个位置，再对剩余元素组成的堆执行上述操作，又会将其中最大的元素放在倒数第二个位置，再对根节点的元素进行下沉操作，如此进行下去就可以排好序了。进行过程如下图所示：

最后再将最后得到的堆（只有两个元素）互换位置即可，这样就是得到一个有序的数组了。从上述过程我们发现，如果初始堆是大根堆我们得到的是升序数组，如果是小根堆的话得到的将是降序数组。

堆排序代码实现

从上述分析过程可以直到每次置换根节点和堆最后一个节点，然后将堆长度减1，然后堆根节点的元素进行下沉操作即可，如此进行下去，直到最后堆中只有一个元素，则排序完成。具体代码如下：

#include 
#include 
#include 
 
#define True 1
#define False 0
#define NUM 9
 
void swap(int * array, int idx1, int idx2) {
    /* 交换数组的两个元素 */
    int t = array[idx1];
    array[idx1] = array[idx2];
    array[idx2] = t;
}
 
void down(int * array, int length, int start, int big=False) {
    while(start < length) {
        int left_child = 2 * start + 1;
        int right_child = 2 * start + 2;
        int idx = left_child;
        if (left_child > length - 1)
            break;
        if(right_child < length) {
            if (!big) {
                if(array[right_child] < array[left_child])
                    idx = right_child;
            } else {
                if(array[right_child] > array[left_child])
                    idx = right_child;
            }
        }
        if(!big) {
            if(array[start] > array[idx]){
                swap(array, idx, start);
                start = idx;
            } else{
                break;
            }
        } else {
            if(array[start] < array[idx]){
                swap(array, idx, start);
                start = idx;
            } else{
                break;
            }
        }
    }
}
 
void heapify(int * array, int length, int start=-2, int big=True) {
 
    if(start == -1)
        return;
    if (start == -2) {
        start = (length - 2) / 2;
    }
    down(array, length, start, big);
    heapify(array, length, start - 1, big);
}
 
 
void heap_sort(int * array, int length, bool reverse=False) {
    for(int i = length - 1; i >=0; i--) {
        swap(array, i, 0);
        down(array, i, 0, !reverse);
    }
}
 
int main() {
    int data[NUM] = {0, 7, 3, 5, 1, 6, 2, 4, 8};
    heapify(data, NUM);
    for(int i=0; i < NUM; i++) {
        printf("%d ", data[i]);
    }
    heap_sort(data, NUM);
    printf("\nAfter sorted !!!\n");
    for(int i=0; i < NUM; i++) {
        printf("%d ", data[i]);
    }
    return 0;
}
 

堆的时间复杂度

从上面堆的结构容易知道，堆是一种二叉树结构，如果当前堆中有元素$N$个，则向堆中插入一个元素的时间复杂度为$O(log(N))$，它在下沉的时候，数据交换的次数不会大于$log(N)$。如果一个数组（堆）中有$N$个元素，那么它需要进行$N$次，根元素和堆的最后一个元素进行交换，然后数据进行下沉，每一次下沉的数据交换次数不会$log(N)$，而且越往后交换的次数距离$log(N)$越大，即交换的次数越来越少，因此堆排序的最大时间复杂度为$O(Nlog(N))$。

优先级队列

队列就是一种先进先出的数据结构，优先级队列就是在队列中优先级最高的先出。如果用一个大于0的整型数字来代表，数据的优先级的话（即数字越小优先级越高）我们可以用小根堆来处理数据，因为小根堆的堆顶元素一定是一个堆中最小的，那么每次进行pop操作，即从队列中拿出一个元素的时候就可以将堆顶的元素和最后一个元素进行交换，然后再将新的堆顶的元素进行下沉操作即可，如果有一个新的元素进行堆，那么它可以现在放在数组最末的位置，然后进行上浮操作，其实这个操作很简单原理和下沉操作一模一样，连停止条件都差不多，他们正好相反，下沉的操作当当前节点是叶子节点或者小于子节点的元素（对于小根堆来说）停止下沉，而上浮操作是当当前节点是根节点或者当前节点的值大于父亲节点就停下来。下面看一个具体的操作过程。

上述一个简单的操作过程。其实很简单，只要掌握了下沉操作这个过程就很容易理解了，以上就是关于堆的所有内容了，如果对你有所帮助，三连~~~

---

以上就是本篇文章的所有内容了，我是LeHung，我们下期再见！！！更多精彩内容合集可访问项目：https://github.com/Chang-LeHung/CSCore

关注公众号：一无是处的研究僧，了解更多计算机（Java、Python、计算机系统基础、算法与数据结构）知识。