关联规则代码实现

1.Apripri算法

        问题：

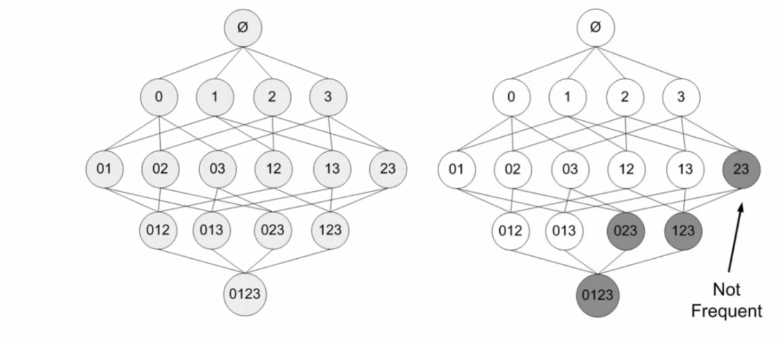
        在探究关联规则时，会得到如图所示的一颗树，每棵树都是一种可能，n个物品的关联一共有2^n-1种可能。这无疑是巨大的运算量

        但是我们可以从中发现一些规律，如果说一个项是非频繁集，那么它的超集也是非频繁集，根据支持度的计算方法，我们可以知道超集的支持度是要小于它本身的项的。因此，项为非频繁集，超级也必定为非频繁集。

        因此，我们可以从上往下进行遍历，并只遍历频繁集的超集

        具体过程为: 

        首先我们遍历一项集，并去掉非频繁集，然后再遍历二巷集，最后，我们再进行一次合并，如图所示，L2的结果有2,3/2,5/3,5,我们就可以合并为（2，3，5）

 

 2.代码实现

        创建数据，首先，我们创建如上图所示的数据

def loadDataSet():
    return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]

         然后我们创建一个冻住的集合，里面包含所有的一元项。

ef createC1(dataSet):
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    return list(map(frozenset,C1))

        对于扫描模块，首先需要计算得到每一个项出现的次数，以求出支持度，并筛选出超过阈值的项集，进行后续的操作。

def scanD(D,CK,minSupport):
    ssCnt = {}
    for tid in D:
        for can in CK:
            if can.issubset(tid):
                if not can in ssCnt: # 项为上面数据的子集
                    ssCnt[can] = 1  # 项不在字典中
                else:
                    ssCnt[can] += 1 # 项在字典中
    numItems = float(len(list(D)))  
    retlist = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key]/numItems
        if support >= minSupport:   # 对项的支持度进行筛选
            retlist.insert(0,key)
        supportData[key] = support
    return retlist,supportData

         拼接操作，如代码所示，对于1项集，L1和L2为空，直接进行拼接。对于二项集，如果第一个项相同，则可以进行拼接操作。

def aprioriGen(LK,k):
    retlist = []
    lenLK = len(LK)
    for i in range(lenLK):
        for j in range(i+1,lenLK):
            L1 = list(LK[i])[:k-2]
            L2 = list(LK[j])[:k-2]
            if L1 == L2:
                retlist.append(LK[i]|LK[j])
    return retlist

        挖掘频繁项集，如上图所示，首先扫描一项集，然后进行拼接，一项集直接拼接，2项集第一项相同也进行拼接。最后更新项集和对应的支持度。

def apriori(dataSet,minSupport=0.5):
    C1 = createC1(dataSet)
    L1,supportData = scanD(dataSet,C1,minSupport)
    L = [L1]
    k = 2    
    while(len(L[k-2]) > 0):
        CK = aprioriGen(L[k-2],k)
        LK,supk = scanD(dataSet,CK,minSupport)
        supportData.update(supk)
        L.append(LK)
        k += 1
    return L,supportData

        规则生成模块，首先，我们需要取出多元项集中的每一项，比如【2,3,5】，取出每一个项，[2],[3],[5]。然后计算置信度。如果是二元项集，如[2,3]，就分别计算[2],[3]和[3],[2]之间的置信度。如果是三元项集，如[2,3,5]，就计算[2]，[3,5]以及[3],[2,5]，[5],[2,3]的置信度。

代码如下：

def generateRules(L,supportData,minConf=0.6):
    rulelist = []
    for i in range(1,len(L)):
        for freqSet in L[i]:
            H1 = [frozenset([item])for item in freqSet]
            rulessFromConseq(freqSet,H1,supportData,rulelist,minConf)
        
    
def rulessFromConseq(freqSet,H,supportData,rulelist,minConf=0.6):   
    m=len(H[0])
    while (len(freqSet) > m):   
        H = calConf(freqSet,H,supportData,rulelist,minConf)
        if (len(H)>1):
            aprioriGen(H,m+1)
            m += 1
        else:
            break
    
def calConf(freqSet,H,supportData,rulelist,minConf=0.6):
    prunedh = []
    for conseq in H:# 置信度的计算
        conf = supportData[freqSet]/supportData[freqSet-conseq]
        if conf >= minConf:
            print (freqSet-conseq,'-->',conseq,'conf:',conf)
            rulelist.append((freqSet-conseq,conseq,conf))
            prunedh.append(conseq)
    return prunedh

        执行代码，结果如下：

if __name__ == '__main__':
    dataSet = loadDataSet()
    L,support = apriori(dataSet)
    i = 0 
    for freq in L:
        print ('项数',i+1,':',freq)
        i+=1
    rules = generateRules(L,support,minConf=0.5)