• 【数据结构】栈和队列重点知识汇总（附有OJ题）

    目录

    思维导图：

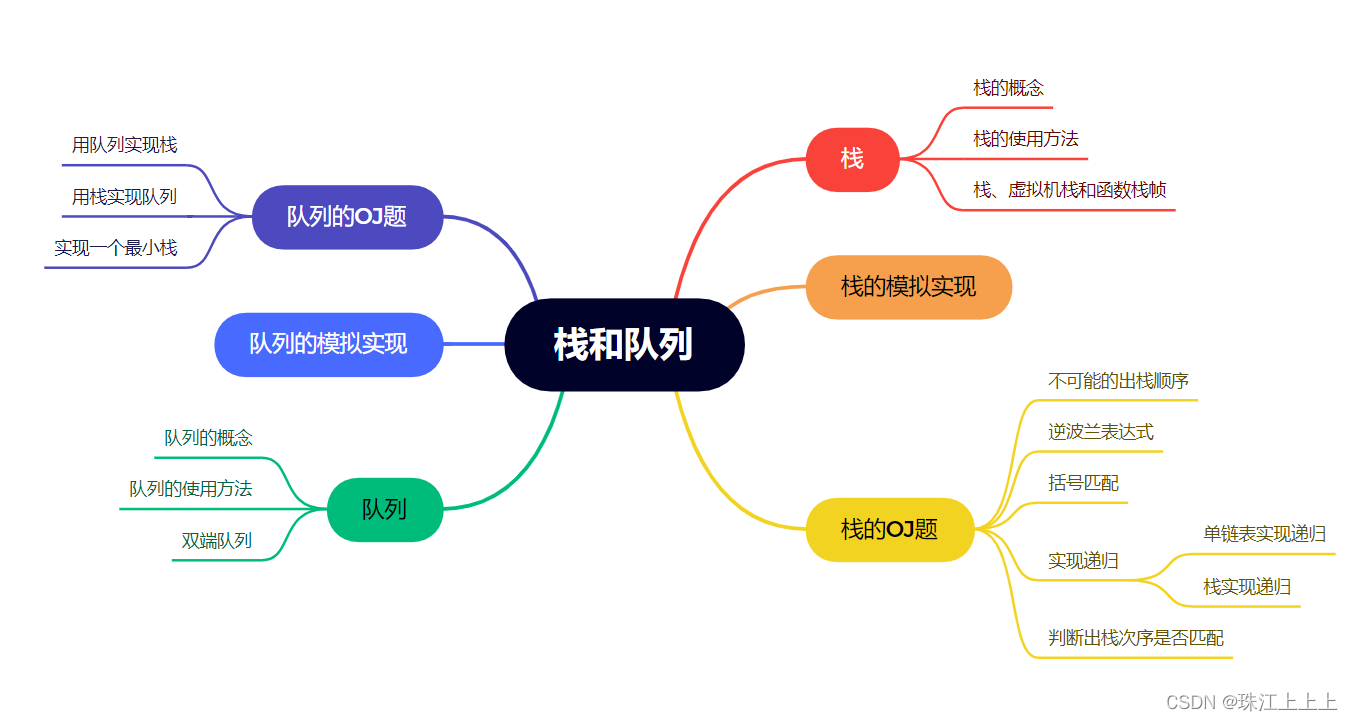
    1.栈（Stack）：

    2.栈的模拟实现：

    3.栈的OJ题：

    4.队列（Queue）：

    5.队列的模拟实现：

    6.队列的OJ题：

    思维导图：

    1.栈（Stack）：

    1. 栈是一种线性表，只允许固定的一端进行插入和删除操作，栈中元素遵循着“先进后出”的原则。往栈中插入元素叫做压栈；栈中弹出删除元素叫做出栈。想象一下装满子弹的弹夹，先装的子弹最后才会被打出去；而最后装的子弹最先打出去，栈就和弹夹的类似。底层上看栈就类似于数组。
    2. 栈的使用方法
      方法作用
      push（x）；压栈，将元素x入栈
      pop（）；出栈，删除栈顶元素
      peek（）；获取栈顶元素，但不删除
      size（）；获取栈中有效的元素个数
      empty（）；检测栈是否为空，空返回 true
    3. 栈和虚拟机栈还有函数栈帧不是一个东西！
       

    2.栈的模拟实现：

    底层是数组实现的

    1. public class MyStack {
    2.     public int[] elem;
    3.     public int usedSize;//存放有效元素个数
    4.     public static final int DEFAULT_CAPACITY = 20;//默认容量
    5.  
    6.     public MyStack(){
    7.         elem = new int[DEFAULT_CAPACITY];
    8.     }
    9.  
    10.     //压栈
    11.     public void push(int data){
    12.         if(isFull()){
    13.             elem = Arrays.copyOf(elem,elem.length*2);
    14.         }
    15.         elem[usedSize] = data;
    16.         usedSize++;
    17.     }
    18.  
    19.     //判断elem有没有满，满了返回true
    20.     private boolean isFull() {
    21.         return elem.length == usedSize;
    22.     }
    23.  
    24.     //判断elem是否为空，空则返回true
    25.     public boolean isEmpty(){
    26.         return usedSize==0;
    27.     }
    28.  
    29.     //删除栈顶元素
    30.     public int pop(){
    31.         if(isEmpty()){
    32.             return -1;
    33.         }
    34.         int oldvalue = elem[usedSize-1];
    35.         usedSize--;
    36.         return oldvalue;
    37.     }
    38.  
    39.     //查看栈顶元素，不删除
    40.     public int peek(){
    41.         if(isEmpty()){
    42.             return -1;
    43.         }
    44.         int ret = elem[usedSize-1];
    45.         return ret;
    46.     }
    47.  
    48.     //获取栈中元素个数
    49.     public int size(){
    50.         return usedSize;
    51.     }
    52.  
    53. }

    3.栈的OJ题：

    1.不可能的出栈顺序：出栈的时候也可以进栈。

    2.逆波兰表达式（往栈中存放数字，遇到符号就从栈中拿出俩个数字，运算后结果放回栈中）。

    1. public class Test {
    2.     public int evalRPN(String[] tokens) {
    3.         Stack stack = new Stack<>();
    4.         for (String x : tokens){
    5.             if(!isOpeation(x)){
    6.                 stack.push(Integer.parseInt(x));
    7.             }else{
    8.                 //num2在+-*/的右边，num1在左边。顺序不能换
    9.                 int num2 = stack.pop();
    10.                 int num1 = stack.pop();
    11.                 switch (x){
    12.                     case "+":
    13.                         stack.push(num1+num2);
    14.                         break;
    15.                     case "-":
    16.                         stack.push(num1-num2);
    17.                         break;
    18.                     case "*":
    19.                         stack.push(num1*num2);
    20.                         break;
    21.                     case "/":
    22.                         stack.push(num1/num2);
    23.                         break;
    24.                 }
    25.             }
    26.         }
    27.         return stack.pop();
    28.     }
    29.  
    30.     private boolean isOpeation(String str) {
    31.         if(str.equals("+")||str.equals("-")
    32.                 ||str.equals("*")||str.equals("/")){
    33.             return true;
    34.         }
    35.         return false;
    36.     }
    37. }

    3.判断括号匹配（判断匹配有俩个条件，字符串遍历完成了；栈为空）。

    1. class Solution {
    2.     public boolean isValid(String s) {
    3.         Stack stack = new Stack<>();
    4.         for (int i = 0; i < s.length(); i++) {
    5.             char ch = s.charAt(i);
    6.             if(ch=='[' || ch=='{' || ch=='('){
    7.                 stack.push(ch);
    8.             }else{
    9.                 //必须要判断栈是否为空，否则会报错
    10.                 if(stack.empty()){
    11.                     return false;
    12.                 }
    13.                 if(ch == ']' && stack.peek() == '['
    14.                         ||ch == '}' && stack.peek() == '{'
    15.                         ||ch == ')' && stack.peek() == '('){
    16.                     stack.pop();
    17.                 }else{
    18.                     return false;
    19.                 }
    20.             }
    21.         }
    22.         //如果栈不为空，则左括号多
    23.         if(stack.empty()){
    24.             return true;
    25.         }else{
    26.             return false;
    27.         }
    28.  
    29.     }
    30. }

    4.实现递归：逆序打印链表。

    1. class Solution {
    2.     //实现递归
    3.     public void printList(ListNode head){
    4.         if(head == null) return;
    5.         if(head.next == null){
    6.             System.out.println(head.val+" ");
    7.             return;
    8.         }
    9.         printList(head.next);
    10.         System.out.println(head.val+" ");
    11.     }
    12.     //栈实现递归,使用到了单链表
    13.     public void printList2(ListNode head){
    14.         Stack stack = new Stack<>();
    15.         ListNode cur = head;
    16.         while(cur != null){
    17.             stack.push(cur);
    18.             cur = cur.next;
    19.         }
    20.         while(!stack.empty()){
    21.             System.out.print(stack.pop());
    22.         }
    23.     }
    24. }

    5.判断出栈次序是否匹配。

    1. public class Solution {
    2.     public boolean IsPopOrder(int [] pushA,int [] popA) {
    3.         if(pushA.length == 0 || popA.length == 0){
    4.             return false;
    5.         }
    6.         Stack stack = new Stack<>();
    7.         int j = 0;
    8.         for (int i = 0; i < pushA.length; i++) {
    9.             stack.push(pushA[i]);
    10.             //特别注意这个循环条件
    11.             while(i < popA.length 
    12.                          && !stack.empty() 
    13.                          //stack.peek()和popA[j]比较时用equal更好，==不严谨
    14.                          && stack.peek().equals(popA[j])){
    15.                 stack.pop();
    16.                 j++;
    17.             }
    18.         }
    19.         return stack.empty();
    20.     }
    21. }

    4.队列（Queue）：

    1. 队列是允许一端进行插入元素和另外一端进行删除操作，队列遵循“先进先出”的原则。类似于大家排队做核酸，先来的人就先做。Queue是一个接口，底层是通过链表实现的；在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。
    2. 队列的使用方法
      方法作用
      offer（x）；将元素x尾插放入队列
      poll（）；将队头元素移出队列，返回改元素
      peek（）；获取队头元素
      size（）；获取队列中有效元素的个数
      isEmpty（）；检测队列是否为空，空返回 true
    3. 双端队列（Deque）：元素可以从队头入队和出队，也可以从队尾出队和入队。

    5.队列的模拟实现：

    底层是由单链表实现的采用链式存储，加上了一个尾节点，这样尾插法入队还是头节点出队时间复杂度都为O(1)。

    1. public class MyQueue {
    2.     static class ListNode{
    3.         public int val;
    4.         public ListNode next;
    5.  
    6.         public ListNode(int val) {
    7.             this.val = val;
    8.         }
    9.     }
    10.     public ListNode head;
    11.     public ListNode last;//队列的尾巴节点
    12.  
    13.     //入队
    14.     public void offer(int data){
    15.         ListNode node = new ListNode(data);
    16.         if(head == null){
    17.             head = node;
    18.             last = node;
    19.         }else{
    20.             last.next = node;
    21.             last = last.next;
    22.         }
    23.     }
    24.  
    25.     //出队
    26.     public int poll(){
    27.         if(head == null){
    28.             return -1;
    29.         }
    30.         int oldvalue = head.val;
    31.         if(head.next == null){
    32.             head = null;
    33.             last = null;
    34.         }else{
    35.             head = head.next;
    36.         }
    37.         return oldvalue;
    38.     }
    39.     //peek()查看当前队头元素是谁
    40.     public int peek(){
    41.         if(head == null){
    42.             return -1;
    43.         }
    44.         return head.val;
    45.     }
    46.     //检查队列是否为空
    47.     public boolean isEmpty(){
    48.         return head == null;
    49.     }
    50.  
    51.     //获取队列中有效元素的个数
    52.     public int size(){
    53.         if(head == null) return 0;
    54.         int count = 0;
    55.         ListNode cur = head;
    56.         while(cur != null){
    57.             count++;
    58.             cur = cur.next;
    59.         }
    60.         return count;
    61.     }
    62.  
    63. }

    6.队列的OJ题：

    1.用队列实现栈（用到俩个队列，俩个队列之间元素的相互调整来实现栈的基本功能）。

    1. public class MyStack {
    2.     //用队列来实现栈
    3.     Queue qu1;
    4.     Queue qu2;
    5.     public int usedSize;
    6.     public MyStack(){
    7.         qu1 = new LinkedList<>();
    8.         qu2 = new LinkedList<>();
    9.     }
    10.  
    11.     //入栈
    12.     public void push(int data){
    13.         if(!qu1.isEmpty()){
    14.             qu1.offer(data);
    15.         } else if (! qu2.isEmpty()) {
    16.             qu2.offer(data);
    17.         }else{
    18.             qu1.offer(data);
    19.         }
    20.         usedSize++;
    21.     }
    22.  
    23.     //出栈
    24.     public int poll(){
    25.         if (empty()) {
    26.             return -1;
    27.         }
    28.         if(! qu1.isEmpty()){
    29.             //size()会发生变化，用cursize记录下来就好
    30.             int cursize = qu1.size();
    31.             for (int i = 0; i < cursize-1; i++) {
    32.                 int ret = qu1.poll();
    33.                 qu2.offer(ret);
    34.             }
    35.             usedSize--;
    36.             return qu1.poll();
    37.         }else{
    38.             int cursize = qu2.size();
    39.             for (int i = 0; i < cursize-1; i++) {
    40.                 int ret = qu2.poll();
    41.                 qu1.offer(ret);
    42.             }
    43.             usedSize--;
    44.             return qu2.poll();
    45.         }
    46.     }
    47.     
    48.     //如果为空返回true
    49.     private boolean empty(){
    50.         return usedSize==0;
    51.     }
    52.  
    53.     //获取栈顶元素
    54.     public int peek(){
    55.         if (empty()) {
    56.             return -1;
    57.         }
    58.         if(! qu1.isEmpty()){
    59.             int cursize = qu1.size();
    60.             int ret = -1;
    61.             for (int i = 0; i < cursize; i++) {
    62.                 ret = qu1.poll();
    63.                 qu2.offer(ret);
    64.             }
    65.             return ret;
    66.         }else{
    67.             int cursize = qu2.size();
    68.             int ret = -1;
    69.             for (int i = 0; i < cursize; i++) {
    70.                 ret = qu2.poll();
    71.                 qu1.offer(ret);
    72.             }
    73.             return ret;
    74.         }
    75.     }
    76. }

    2.用栈实现队列（用到俩个栈，将元素从一个栈转到另外一个栈从而完成队列的基本功能）。

    1. //用栈来模拟实现队列
    2. public class MyQueue {
    3.     Stack s1;
    4.     Stack s2;
    5.     public MyQueue(){
    6.         s1 = new Stack<>();
    7.         s2 = new Stack<>();
    8.     }
    9.  
    10.     //入队
    11.     public void offer(int data){
    12.         s1.push(data);
    13.     }
    14.  
    15.     //出栈
    16.     public int pop(){
    17.         if(isEmpty()){
    18.             return -1;
    19.         }
    20.         if(s2.empty()){
    21.             while(!s1.empty()){
    22.                 s2.push(s1.pop());
    23.             }
    24.         }
    25.         return s2.pop();
    26.     }
    27.  
    28.     //查看队头元素
    29.     public int peek(){
    30.         if(isEmpty()){
    31.             return -1;
    32.         }
    33.         if(s2.empty()){
    34.             while(!s1.empty()){
    35.                 s2.push(s1.pop());
    36.             }
    37.         }
    38.         return s2.peek();
    39.     }
    40.  
    41.     //检查元素是否为空，空返回
    42.     public boolean isEmpty(){
    43.         return s1.empty() && s2.empty();
    44.     }
    45.     
    46.     
    47. }

    3.实现一个最小栈（用到俩个栈，一个存放push进来的元素，一个存放最小的元素）。

    1. public class MinStack {
    2.     Stack s;
    3.     Stack minStack;
    4.     
    5.     public MinStack(){
    6.         s = new Stack<>();
    7.         minStack = new Stack<>();
    8.     }
    9.     
    10.     //入栈
    11.     public void push(int data){
    12.         s.push(data);
    13.         if(minStack.empty()){
    14.             minStack.push(data);
    15.         }else{
    16.             if(minStack.peek() >= data){
    17.                 minStack.push(data);
    18.             }
    19.         }
    20.     }
    21.     
    22.     //出栈
    23.     public void pop(){
    24.         if(!s.empty()) {
    25.             int popV = s.pop();
    26.             int minV = minStack.peek();
    27.             if (popV == minV) {
    28.                 minStack.pop();
    29.             }
    30.         }
    31.     }
    32.     
    33.     //获取栈顶元素，不是删除
    34.     public int peek(){
    35.         if(!s.empty()){
    36.             return s.peek();
    37.         }
    38.         return -1;
    39.     }
    40.     
    41.     //获取栈顶最小元素
    42.     public int peekmin(){
    43.         if(!minStack.empty()){
    44.             return minStack.peek();
    45.         }
    46.         return -1;
    47.     }
    48. }

    如果对您有帮助的话，

    不要忘记点赞+关注哦，蟹蟹

    如果对您有帮助的话，

    不要忘记点赞+关注哦，蟹蟹

    如果对您有帮助的话，

    不要忘记点赞+关注哦，蟹蟹

  • 相关阅读:
    23种设计模式之创建型模式篇
    【学习记录】autoware标定相机与激光雷达外参
    2022/7/27 考试总结
    集成crawlergo和xray的src漏洞挖掘利器（hscan）
    Linux下的多线程编程：原理、工具及应用（2）
    二十、一起学习Lua 面向对象
    java 上机练习题
    GDB符号表概念及Linux获取符号表的方式
    维视智造x西安电子科技大学，联合授课助力AI产业人才培养
    环状分组柱状图 Python
  • 原文地址：https://blog.csdn.net/qq_68993495/article/details/127033640