二叉树——堆的排序 TOP-K算法

堆的排序

这里排序无非就是升序和降序，那么，之前用的冒泡排序时间复杂度是很高的，所以这次来了解一个更加高效率的。

建堆

建堆的过程有两种，一是向上调整法，另一种是向下调整法，但是更快的是向下调整法，因为堆是类似于一个三角形，越往下，元素就越多，向上调整，堆顶的结点一定不用在向上调整了，因为堆顶上面没有父节点了，而向下调整法是叶子结点不用在向下调整了，因为叶子结点是最后的结点，下面没有子结点。
那么，肯定是向下调整法的时间复杂度比较低。
代码实现

void swap(int* p1, int* p2)//交换数据
{
	int p = *p1;
	*p1 = *p2;
	*p2 = p;
}
void upward(int* a,int size,int parent)//向下调整
{
	int minchild = 2 * parent + 1;//表示最小的孩子，第一次先假设左孩子最小
	while (minchild < size)//防止数组越界
	{
		if (minchild + 1 < size && a[minchild + 1] > a[minchild])//防止右孩子出界
		{
			minchild++;//如果右孩子比左孩子小就让右孩子等于最小
		}
		if (a[minchild] > a[parent])//判断是否需要向下调整
		{
			swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
void sort()
{
	int arr[] = { 10,6,3,4,9,10,81 };//随机数组
	int n = sizeof(arr) / sizeof(arr[0]);//数组有效数的长度
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//这里(n-1-1)/2是因为找下标需要-1，然后剩下公式的是找到最后一个叶子节点的父母
	{//遍历除叶子结点外所有结点
		upward(arr, n, i);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

利用堆删除思想来进行排序

建堆的时间复杂度是O(N)，之前说过向下查找法和向上查找法，时间复杂度是O(logN).
大堆是父结点比子结点大，小堆则相反，我们用堆排序的核心思路是类似于删除的逻辑，因为在堆顶不是最大的就是最小的，我们把堆顶的元素和尾部交换然后再进行排序就可以了。
那么，降序要用小堆，升序用大堆。
例：降序，图像理解


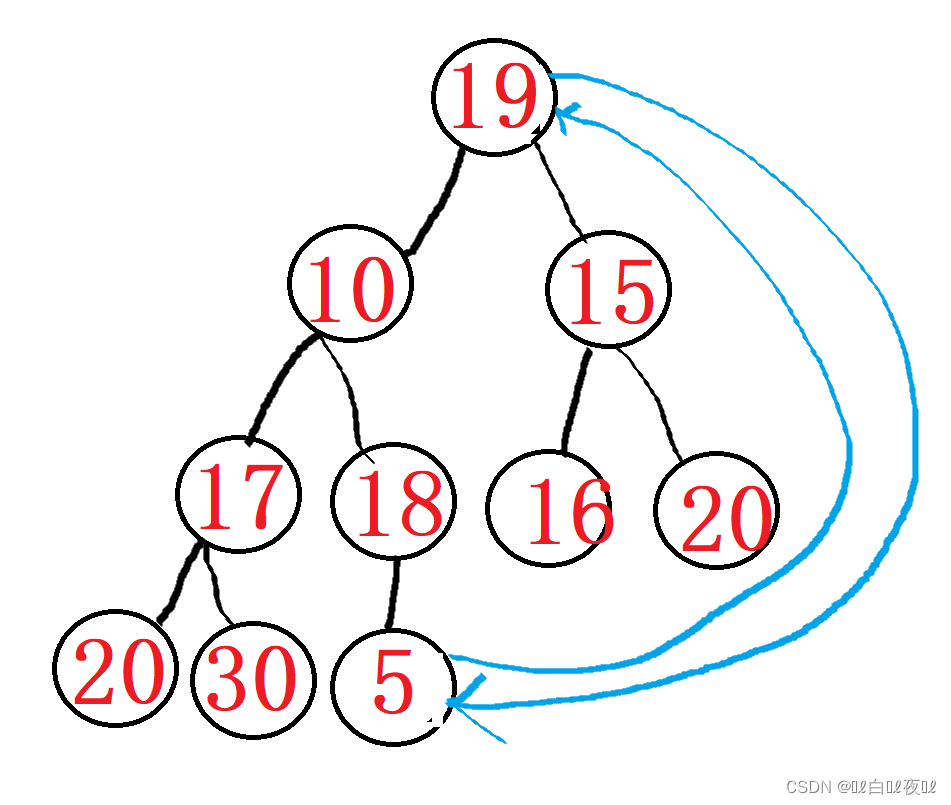
然后让5之前的数进行向下调整，从而不打乱小堆的结构。

再让堆顶的10与30交换

最后以此类推。
例：升序，代码实现

void swap(int* p1, int* p2)//交换数据
{
	int p = *p1;
	*p1 = *p2;
	*p2 = p;
}
void upward(int* a,int size,int parent)//向下调整
{
	int maxchild = 2 * parent + 1;//表示最大的孩子，第一次先假设左孩子最小
	while (maxchild < size)//防止数组越界
	{
		if (maxchild + 1 < size && a[maxchild + 1] > a[maxchild])//防止右孩子出界
		{
			maxchild++;//如果右孩子比左孩子大就让右孩子等于最大
		}
		if (a[maxchild] > a[parent])//判断是否需要向下调整
		{
			swap(&a[maxchild], &a[parent]);
			parent = maxchild;
			maxchild = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
void sort()
{
	int arr[] = { 10,6,3,4,9,10,81 };//随机数组
	int n = sizeof(arr) / sizeof(arr[0]);//数组有效数的长度
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//这里(n-1-1)/2是因为找下标需要-1，然后剩下公式的是找到最后一个叶子节点的父母
	{//遍历除叶子结点外所有结点
		upward(arr, n, i);//建大堆
	}
	int i = 1;
	while (i < n)//因为最终要排序n-1次
	{
		swap(&arr[0],&arr[n-i]);//交换首尾
		upward(arr, n - i, 0);//向下调整，保持小堆
		++i;
	}
	int j = 0;
	for (j = 0; j < n; ++j)
	{
		printf("%d ", arr[j]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

TOP-K算法

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
对于Top-K问题，能想到的最简单直接的方式就是排序O(N*logN)，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

用数据集合中前K个元素来建堆

假如数组里面的数有N个（非常大），然后找K（非常小）前面的元素，那么就用建立大堆然后再进行删除的操作，也就是首尾交换。
例如：如果是寻找数组中前K个最大元素，那么时间复杂度就是建堆和找数的时间，找数只要找K次就可以了。O(N+logN*K)
但是如果N很大，K很小时间复杂度也是很高，所以这里创建小堆。
小堆方法
用数组中前K个数建立一个小堆，小堆的容量也就是我们需要的数量，这时就需要交换小堆里面的数了，因为堆顶的数是最小的，所以我们遍历K后面的数，也就是N-K个数，如果比堆顶的大就和堆顶交换，之后再进行向下调整。

时间复杂度为O(K+logK*(N-K))
因为K很小的原因，所以就约等于O(N)
结论如下：

1. 前k个最大的元素，则建小堆
2. 前k个最小的元素，则建大堆

用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
代码实现

void swap(int* p1, int* p2)//交换数据
{
	int p = *p1;
	*p1 = *p2;
	*p2 = p;
}
void upward(int* a,int size,int parent)//向下调整
{
	int minchild = 2 * parent + 1;//表示最小的孩子，第一次先假设左孩子最小
	while (minchild < size)//防止数组越界
	{
		if (minchild + 1 < size && a[minchild + 1] < a[minchild])//防止右孩子出界
		{
			minchild++;//如果右孩子比左孩子小就让右孩子等于最小
		}
		if (a[minchild] < a[parent])//判断是否需要向下调整
		{
			swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
void random(char* p, int n)//向文件中写入随机数
{
	FILE* p1 = fopen(p, "w");//写文件，让p1指向文件位置
	if (p1 == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	srand(time(0));//随机数的起点
	for (int i = 0; i < n; ++i)//向文件中写入随机数
	{
		fprintf(p1, "%d ", rand()%1000);//这里不让随机数超过1000方便观看
	}
	fclose(p1);
}
void TestTopk(char* p, int k)
{
	FILE* p1 = fopen(p, "r");//打开文件，让p1指向文件位置
	if (p1 == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	int* p2 = (int*)malloc(sizeof(int) * k);//开辟堆的空间
	if (p2 == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	for (int i = 0; i < k; i++)//读取k之前的数
	{
		fscanf(p1, "%d", &p2[i]);//把文件前k歌数读取到新建堆中
	}
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{
		upward(p2, k, j);//建小堆
	}
	int a = 0;
	while (fscanf(p1, "%d", &a) != EOF)//读取K之后的数
	{
		if (a > p2[0])
		{
			p2[0] = a;
			upward(p2, k, 0);//向下调整
		}
	}
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", p2[i]);//打印k之前的数据
	}
	fclose(p1);
	free(p2);
}

int main()
{
	const char* p = "TOP-K.txt";//自己创建一个文件
	int k = 10;
	int n = 100;
	random(p, n);
	TestTopk(p, k);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90