【目标跟踪-卡尔曼滤波】基于分布式Kalman滤波跟踪运动目标附Matlab代码

1 内容介绍

近年来，随着工业的发展，对于一些实际模型的建立所提出的要求也越来越高。作为对传统整数阶微积分学的一种扩展，分数阶微积分能实现对实际系统的更为准确的描述。目前，分数阶微积分在冶金、化工、电力、轻工和机械等工业过程中都有着广泛的应用，它的发展也为各个学科的发展提供了新的理论基础。

​

SISO分数阶系统的分数卡尔曼滤波器算法源代码，包括：分数扩展卡尔曼滤波器（FEKF）、分数中心卡尔曼滤波器（FCDKF）、分数无迹卡尔曼滤波器（FUKF）和分数粒子滤波器（FPF）

2 部分代码

%*************************************************************************%

%                      无迹卡尔曼滤波器仿真复现                           %

%_________________________________________________________________________%

%   论文 : 非线性系统滤波理论 P108 5.4.2 强非线性系统模型仿真

%   目的 : 无迹卡尔曼滤波器仿真复现

%   函数实验 ::

%                   | 3*sin(2*x_2)                 |   | 1 |

%             x_k = | x_1 + exp(-0.05x_3) + 10     | + | 1 |w_k

%                   | = x_1(x_2 + x_3)/5 + |x_1|/2 |   | 1 |

%

%   结果 : 滤波效果良好

%

%   备注 : 

%

%*************************************************************************%

clc

clear

%仿真步长

N = 50;

q = 0.3;                %系统噪声均值

r = 0.5;                %测量噪声均值

Q = 0.7;                %系统噪声方差矩阵

R = 1.0;                %测量噪声方差矩阵

% %GL定义下短记忆原理的长度

% L = N+1;

% %计算alpha阶次对应的GL定义系数 binomial coefficient 

% bino_fir = zeros(1,N);       %微分阶次为0.7时GL定义下的系数

% alpha = 0.7;

% bino_fir(1,1) = 1;

% for i = 2:1:N

%     bino_fir(1,i) = (1-(alpha+1)/(i-1))*bino_fir(1,i-1);  

% end

I = eye(3,3);                %生成单位阵

%err_state_FEKF  = zeros(kk_N,N);

X_state_real = zeros(3,N);         %真实状态

Z_state_meas = zeros(1,N);         %实际观测值

%噪声

W_noise = sqrt(Q)*randn(1,N) + q;  %系统噪声

V_noise = sqrt(R)*randn(1,N) + r;  %测量噪声

x_0  = [-0.7; 1; 1];               %初始状态     

X_state_real(:,1) = x_0;           %真实状态初始值

Z_state_meas(1,1) = V_noise(1,1);  %测量数据初始值

f=@(x)[3*sin(2*x(2)); ...

       x(1) + exp(-0.05*x(3)) + 10; ...

       0.2 * x(1) * (x(2) + x(3)) + 0.5*abs(x(1)) ];

h=@(x)x(1) + x(2) * x(3);

   

for k=2:1:N

    %计算实际状态

    X_state_real(:,k) = f(X_state_real(:,k-1)) + [1; 1; 1] * W_noise(1,k-1);

        

    %实际观测值

    Z_state_meas(1,k) = h(X_state_real(:,k)) + V_noise(1,k); 

end

%*************************************************************************%

%-------------------------无迹卡尔曼滤波器性能测试------------------------%

%*************************************************************************%

X_state_esti = zeros(3,N);      %状态最优估计值

P_xesti      = cell(1,N);      %估计误差方差阵

%初始值设置（初始矩阵不能为零）

P_pred_0     = eye(3,3);        %初始预测方差阵

P_xesti{1,1} = P_pred_0;        %初始估计方差阵

state_dim = 3;

L_sample  = 2 * state_dim +1;

SigmaPoints = zeros(3, L_sample);

SigmaWeight = zeros(1, L_sample);

GammaPoints = zeros(3, L_sample);

ChiPoints   = zeros(1, L_sample);

%*******************************%

%   画图输出 均值方差估计散点图

%*******************************%

%输入与测量输出图

k = 1:1:N;

LineWidth = 1.5;

%square error

figure;

plot(k,X_state_real(3,:),'r',k,X_state_esti(3,:),'b--','linewidth',LineWidth);

%set(gcf,'Position',[200 200 400 300]); 

%axis([xmin xmax ymin ymax])设置坐标轴在指定的区间

% axis normal

% axis([ -10 N 0 6 ])

ylabel('$x_3$','FontSize',8)

xlabel('time(sec)','FontSize',8)

%设置坐标轴刻度字体名称，大小

set(gca,'FontName','Helvetica','FontSize',8)

legend('real state','estimated state','Location','best');

legend('Real state 3','Estimation state 3','Location','best');

figure;

plot(k,X_state_real(2,:),'r',k,X_state_esti(2,:),'b--','linewidth',LineWidth);

%set(gcf,'Position',[200 200 400 300]); 

%axis([xmin xmax ymin ymax])设置坐标轴在指定的区间

% axis normal

% axis([ -10 N 0 6 ])

ylabel('$x_3$','FontSize',8)

xlabel('time(sec)','FontSize',8)

%设置坐标轴刻度字体名称，大小

set(gca,'FontName','Helvetica','FontSize',8)

legend('real state','estimated state','Location','best');

legend('Real state 2','Estimation state 2','Location','best');

figure;

plot(k,X_state_real(1,:),'r',k,X_state_esti(1,:),'b--','linewidth',LineWidth);

%set(gcf,'Position',[200 200 400 300]); 

%axis([xmin xmax ymin ymax])设置坐标轴在指定的区间

% axis normal

% axis([ -10 N 0 6 ])

ylabel('$x_3$','FontSize',8)

xlabel('time(sec)','FontSize',8)

%设置坐标轴刻度字体名称，大小

set(gca,'FontName','Helvetica','FontSize',8)

legend('real state','estimated state','Location','best');

legend('Real state 1','Estimation state 1','Location','best');

3 运行结果

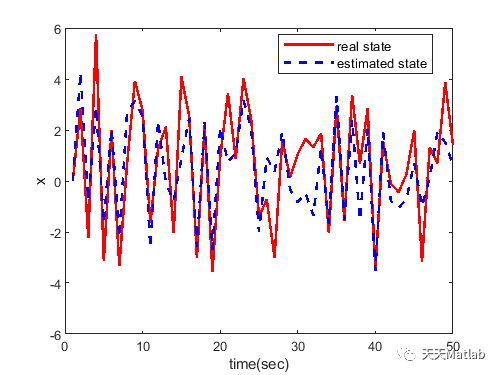
4 参考文献

[1]陈林. 一种基于卡尔曼滤波的运动目标跟踪方法[J]. 舰船电子对抗, 2011, 034(003):67-70.

[2]王雯洁, 汪非易, 赵航芳. 基于分布式传感器能量比的水下运动目标扩展卡尔曼滤波跟踪方法:, 2018.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机、雷达通信、无线传感器等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。