-
链式二叉树【递归】
我们前面已经了解了树和堆的性质原理,今天就来学习一下链式二叉树,也就是递归
前言
下面是我们前面讲的树、二叉树和堆的一些性质:
其次,我们在下面实现二叉树要使用到队列的代码
普通二插树的实现
1、构建一个二叉树
方法1
我们在拿到一组数据的时候,这组数据在逻辑结构上面并不是一个二叉树,这里为了方便直接手动构建一个二叉树
通过前序遍历的数组"123#7###45##6##"构建二叉树
BTNode* BinaryTreeCreate1() { BTNode* n1 = (BTNode*)malloc(sizeof(BTNode)); assert(n1);//为了方便直接断言n1,后面同理 BTNode* n2 = (BTNode*)malloc(sizeof(BTNode)); assert(n2); BTNode* n3 = (BTNode*)malloc(sizeof(BTNode)); assert(n3); BTNode* n4 = (BTNode*)malloc(sizeof(BTNode)); assert(n4); BTNode* n5 = (BTNode*)malloc(sizeof(BTNode)); assert(n5); BTNode* n6 = (BTNode*)malloc(sizeof(BTNode)); assert(n6); BTNode* n7 = (BTNode*)malloc(sizeof(BTNode)); assert(n7); n1->data = 1; n2->data = 2; n3->data = 3; n4->data = 4; n5->data = 5; n6->data = 6; n7->data = 7; n1->left = n2; n1->right = n4; n2->left = n3; n2->right = NULL; n3->left = NULL; n3->right = n7; n4->left = n5; n4->right = n6; n5->left = NULL; n5->right = NULL; n6->left = NULL; n6->right = NULL; n7->left = NULL; n7->right = NULL; return n1; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
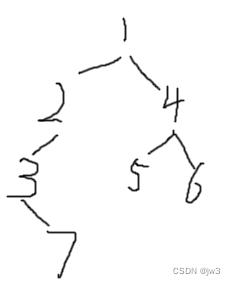
这样就构成了一个简单的二叉树接下来换一种方法进行构建二叉树
方法2
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树 BTNode* BinaryTreeCreate2(char* a, int* pi)//这里的*pi是下标,如果不使用下标在特殊情况下*pi下标对应的值会被后面的值给覆盖了 { if (a[*pi] == '#')//如果数组里面的元素是#,那么下标*pi就加加,到下一位 { (*pi)++; return NULL; } BTNode* root = (BTNode*)malloc(sizeof(BTNode));//动态开辟root if (root == NULL) { perror("malloc fail\n"); exit(-1); } root->data = a[(*pi)++];//二叉树的节点值就等于数组a里面的元素 root->left = BinaryTreeCreate2(a, pi);//左子树递归 root->right = BinaryTreeCreate2(a, pi);//右子树递归 return root;//返回root就是返回我们构建出来的二叉树的起始地址 } char a[18] = "ABD##E#H##CF##G##"; int pi = 0; //BTNode* root = BinaryTreeCreate2(a, &pi); root = BinaryTreeCreate2(a, &pi); BinaryTreePrevOrder(root);//要用%c遍历- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
2、遍历操作
普通二叉树不像特殊二叉树和堆那样,它的函数接口并不是增删查改,因为普通二叉树进行增删查改没有意义
普通二叉树最常见的操作就是前序遍历、中序遍历、后序遍历和层序遍历
我们先来看看前面的三种遍历:学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉
树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历
是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:1 . 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。由于被访问的结点必是某子树的根,所以N(Node)、 L(Left subtree)和R(Right subtree)又可解释为
根、根的左子树和根的右子树。 NLR、 LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。也就是说三种遍历的操作顺序为:
前序遍历:根——左子树——右子树
中序遍历:左子树——根——右子树
后序遍历:左子树——右子树——根这里我们来看看前序遍历,中序遍历和后序遍历也会融会贯通的
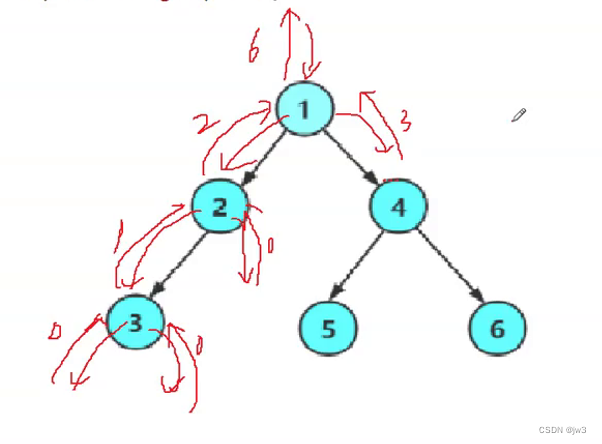
前序遍历递归图解:
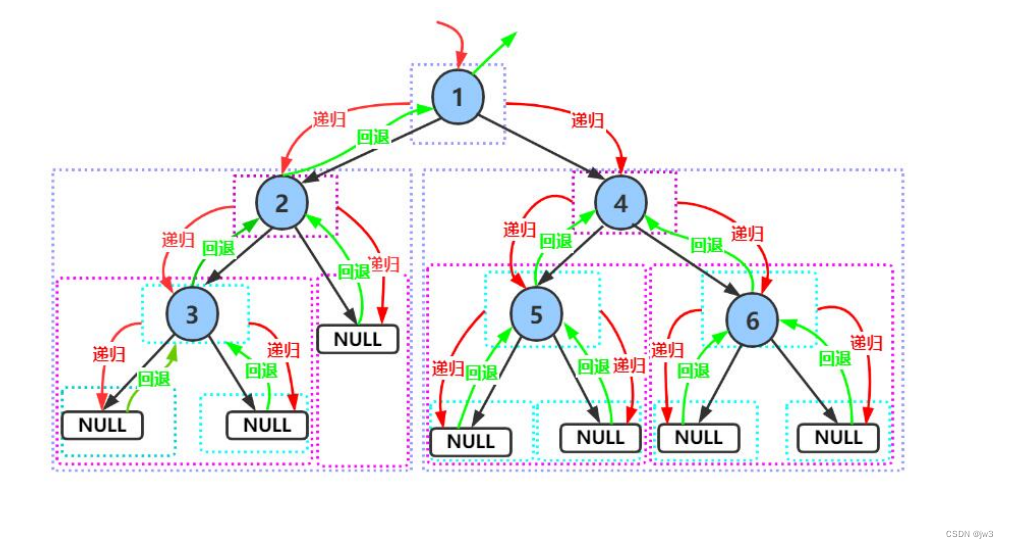

接下来看看前、中、后序遍历的代码:
// 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } printf("%d ", root->data); BinaryTreePrevOrder(root->left); BinaryTreePrevOrder(root->right); } // 二叉树中序遍历 void BinaryTreeInOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } BinaryTreeInOrder(root->left); printf("%d ", root->data); BinaryTreeInOrder(root->right); } // 二叉树后序遍历 void BinaryTreePostOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } BinaryTreePostOrder(root->left); BinaryTreePostOrder(root->right); printf("%d ", root->data); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
这里我们通过递归展开图来分析:
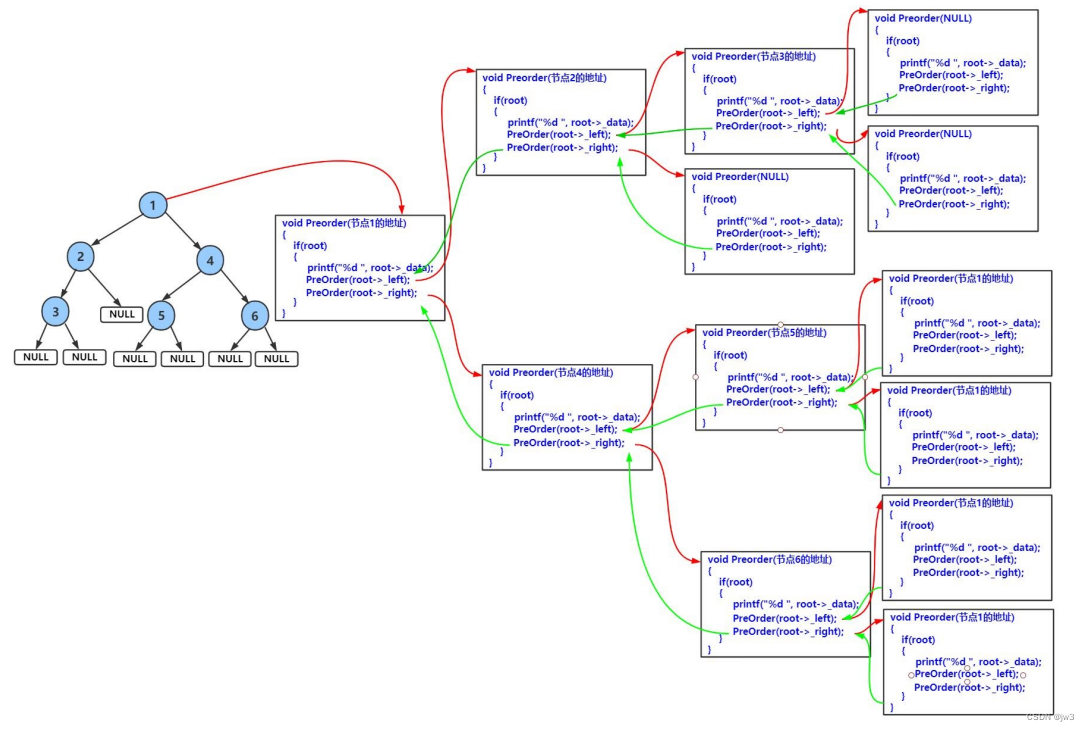
上面就是前序遍历的递归展开图,中序遍历和后序遍历与上面差不多,大家可以自己动手画一画接下来我们看看层序遍历,这里就要用到一个队列来完成了。因为用队列会比较简单
主要逻辑就是:上一层节点出的时候带入下一层节点

这里就是QueueNode里面包含了一个BTNode*
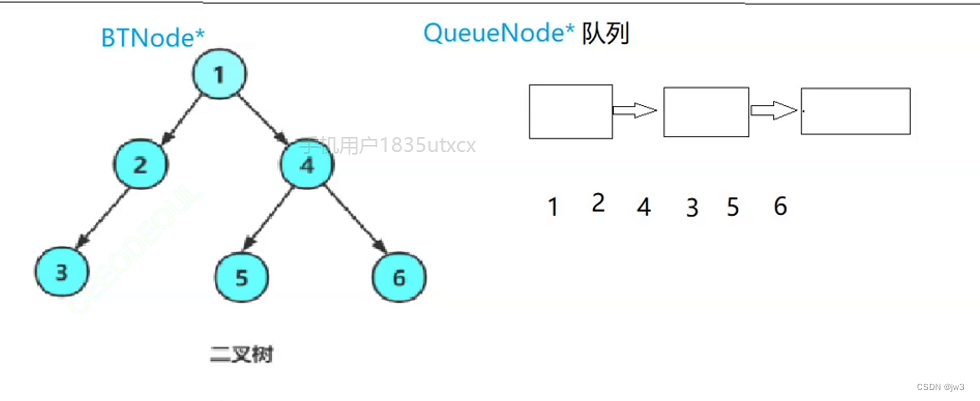
代码如下:
// 层序遍历 void BinaryTreeLevelOrder(BTNode* root) { Queue p; QueueInit(&p); if (root)//如果树的节点不为空,就先把树的节点入进去 QueuePush(&p, root); while (!QueueEmpty(&p))//如果队列不为空 { BTNode* front = QueueFront(&p);//出队头数据 QueuePop(&p); printf("%d ", front->data);//打印 if (front->left)//上一层节点出的时候,带下一层左节点 QueuePush(&p, front->left); if (front->right)//上一层节点出的时候,带下一层右节点 QueuePush(&p, front->right); } printf("\n"); QueueDestroy(&p); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
3、二叉树的销毁
这个挺简单的,也是左右递归下去然后free掉root
// 二叉树销毁 void BinaryTreeDestory(BTNode* root) { if (root == NULL) return; BinaryTreeDestory(root->left); BinaryTreeDestory(root->right); free(root); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
4、节点个数
// 二叉树节点个数 int BinaryTreeSize(BTNode* root) { return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; //如果root不等于NULL,那么就返回左子树节点与右子树节点加上1的和,就是整个二叉树节点个数 }- 1
- 2
- 3
- 4
- 5
- 6
注意:
这里如果使用一个计数器的话有许多弊端的。如果使用局部变量计数器那么就不会返回,因为局部变量计数器出作用域就销毁了,外面接收返回值就相当于越界访问了;如果加static变为静态变量也有问题,局部的静态变量只有在第一次调用的时候会初始化,static修饰的变量是保存在静态区的,这个变量在函数销毁之后并不会销毁,那么如果多次求二叉树节点个数结果会不断累加
同一棵树调用两次求节点个数:

可以看到结果是累加的,所以使用static修饰的静态变量也有问题
如果使用全局变量计数的话,在每次统计个数的时候记得把全局变量初始化为0,不然结果也是累加的
5、叶节点的个数
// 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL)//如果节点的左子树和右子树都为空,那么该节点就是叶子节点,返回1 return 1; return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);//左子树的叶子节点加上右子树的叶子节点 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
6、树高
//二叉树高度/层次 int BinaryTreeHeight(BTNode* root)//这里的函数是有返回值的,所以左右子树递归结果要用一个int变量进行统计 { if (root == NULL) return 0; int leftheight = BinaryTreeHeight(root->left);//如果这里没有leftheight和下面的rightheight就接收不到左右子树的返回结果 int rightheight = BinaryTreeHeight(root->right); return leftheight > rightheight ? leftheight + 1 : rightheight + 1; //因为是求树高,所以左右子树高度高的那一个加上根就是整个树的高度 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
7、第k层的节点个数
// 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k) { assert(k > 0); if (root == NULL) return 0; if (k == 1)//如果k等于1,就直接返回1,因为左右子树递归到第k层的时候有且仅有一个节点 return 1; return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1); //左右递归,k依次减一,表示每次递归一层 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
8、查找x节点
// 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, NDataType x)//与上面一样,函数有返回值的 { if (root == NULL) return NULL; if (root->data == x)//如果data等于x,直接返回root当前的地址 return root; BTNode* left = BinaryTreeFind(root->left, x);//这里和下面都需要一个BTNode指针类型来接收左右子树递归返回的地址 //if(left) //return left; BTNode* right = BinaryTreeFind(root->right, x); //if(right) //return right; //return NULL; return left == NULL ? right : left; //这里是一个小妙招,如果left等于NULL,就返回right地址;即便是right是NULL,返回right也没错,因为left是NULL }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
9、判断二叉树是否是完全二叉树
思路:
使用层序遍历方法,上一层节点出的时候带下一层节点,当出的节点为NULL时,后面数据必须都为NULL,否则就是错的
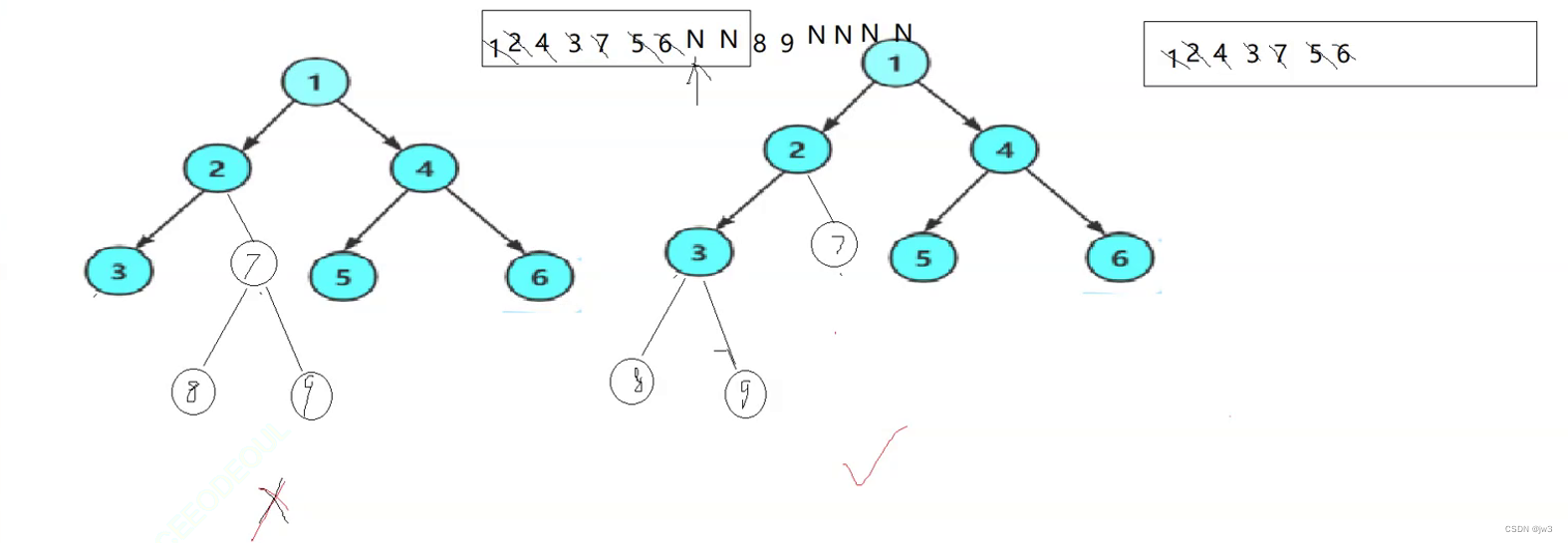
// 判断二叉树是否是完全二叉树 // 判断二叉树是否是完全二叉树(使用层序遍历方法) int BinaryTreeComplete(BTNode* root) {//与上面一样,上一层节点出的时候带下一层节点,当出的节点为NULL时,后面数据必须都为NULL,否则就是错的 Queue p; QueueInit(&p); if (root)//如果树的节点不为空,就先把树的节点入进去 QueuePush(&p, root); while (!QueueEmpty(&p)) { BTNode* front = QueueFront(&p); QueuePop(&p); if (front == NULL)//当出到NULL的时候就跳出 break; QueuePush(&p, front->left); QueuePush(&p, front->right); } while (!QueueEmpty(&p))//到这里如果后面全是NULL,那么是完全二叉树 { BTNode* front = QueueFront(&p); QueuePop(&p); if (front != NULL) { QueueDestroy(&p);//记得销毁 return false;//如果后面有一个数据不是NULL,那么就不是完全二叉树 } } QueueDestroy(&p); return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
前全部代码
这里代码大部分都有注释,应该比较容易理解
Queue.h
#pragma once #include#include #include #include typedef int NDataType; typedef struct BinaryTreeNode { NDataType data; struct BinaryTreeNode* left; struct BinaryTreeNode* right; }BTNode;//这里要把二叉树结构体定义放到这里,因为Queue.c也引用了Queue.h头文件,如果不放到这里,Queue.c无法使用下面的DataType typedef BTNode* DataType;//这里不再是int重命名了,而是BTNode*类型重命名 //QueueNode*里面包含了一个BTNode* typedef struct QueueNode//单链表的形式 { DataType data;//数值 struct QueueNode* next;//指向下一个节点的指针 }QN;//重命名为QN typedef struct Queue//定义一个结构体用来存放两个结构体指针 //这样修改外面指针(也就是改变head和tail指向节点)的时候,不用传二级指针和接收改变指针的返回值 { QN* head;//指向队列的对头 QN* tail;//指向队列的对尾 int size;//记录队列数据个数,用一个计数器可以提高计算效率 }Queue; void QueueInit(Queue* ps);//初始化 void QueueDestroy(Queue* ps);//释放空间 bool QueueEmpty(Queue* ps);//判断队列是否为空 void QueuePush(Queue* ps,DataType x);//入队列 void QueuePop(Queue* ps);//出队列 DataType QueueFront(Queue* ps);//队头数据 DataType QueueBack(Queue* ps);//队尾数据 int QueueSize(Queue* ps);//队列剩余数据个数 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
Queue.c
#define _CRT_SECURE_NO_WARNINGS #include"Queue.h" void QueueInit(Queue* ps)//初始化 { assert(ps); ps->head = ps->tail = NULL;//两个指针都指向空 ps->size = 0;//此时队列没有数据 } void QueueDestroy(Queue* ps)//释放空间 { assert(ps); QN* cur = ps->head;//cur等于头指针,ps是结构体指针,结构体指针指向头指针 while (cur)//如果头指针不为空,就进入循环释放空间 { QN* del = cur;//保留头指针的节点 cur = cur->next;//头指针向后移动 free(del);//释放头指针移动前的节点 } ps->head = ps->tail = NULL;//释放完之后,头尾指针指向NULL ps->size = 0;//数据个数清0 } void QueuePush(Queue* ps, DataType x)//入队列 { assert(ps); QN* newnode = (QN*)malloc(sizeof(QN));//扩容一个新的节点出来 if (newnode == NULL) { perror("malloc fail\n"); exit(-1); } else { newnode->data = x;//对新节点就行初始化操作 newnode->next = NULL;//这里将新节点的next置空,不用考虑插入节点后的next指向了 } if (ps->tail == NULL)//第一次入队列数据head和tail都是指向NULL的,直接让head和tail都指向第一个新节点 { ps->head = ps->tail = newnode; } else { ps->tail->next = newnode;//将扩容节点插在tail后面 ps->tail = newnode;//让tail指向到插入的节点处 } ++ps->size;//插入size就加1,记录此时队列节点的个数 } void QueuePop(Queue* ps)//出队列(队列出数据就相当于单链表的头删) { assert(ps); assert(!QueueEmpty(ps));//如果队列没有节点了,断言生效 if(ps->head->next==NULL)//如果队列只剩下一个节点了,直接释放该节点,然后将头尾指针置空 { free(ps->head); ps->head = ps->tail = NULL; } else { QN* cur = ps->head;//保存当前头节点 ps->head = ps->head->next;//让头指针指向下一个节点 free(cur);//释放之前的头节点 cur = NULL; } --ps->size;//出一个数据size就减1 } bool QueueEmpty(Queue* ps)//判断队列是否为空 { assert(ps); return ps->head == NULL && ps->tail == NULL;//头尾指针都指向NULL,队列才为空 } DataType QueueFront(Queue* ps)//队头数据 { assert(ps); assert(!QueueEmpty(ps)); return ps->head->data; } DataType QueueBack(Queue* ps)//队尾数据 { assert(ps); assert(!QueueEmpty(ps)); return ps->tail->data; } int QueueSize(Queue* ps)//队列剩余数据个数 { assert(ps); return ps->size; /*QN* cur = ps->head;//不使用size的方法,遍历队列,如果偶尔查看数据个数还好,经常使用效率太慢了 int capacity = 0; while (cur) { ++capacity; cur = cur->next; } return capacity;*/ }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
Test.c
#define _CRT_SECURE_NO_WARNINGS #include"Queue.h" // 通过前序遍历的数组"123#7###45##6##"构建二叉树 BTNode* BinaryTreeCreate1() { BTNode* n1 = (BTNode*)malloc(sizeof(BTNode)); assert(n1); BTNode* n2 = (BTNode*)malloc(sizeof(BTNode)); assert(n2); BTNode* n3 = (BTNode*)malloc(sizeof(BTNode)); assert(n3); BTNode* n4 = (BTNode*)malloc(sizeof(BTNode)); assert(n4); BTNode* n5 = (BTNode*)malloc(sizeof(BTNode)); assert(n5); BTNode* n6 = (BTNode*)malloc(sizeof(BTNode)); assert(n6); BTNode* n7 = (BTNode*)malloc(sizeof(BTNode)); assert(n7); n1->data = 1; n2->data = 2; n3->data = 3; n4->data = 4; n5->data = 5; n6->data = 6; n7->data = 7; n1->left = n2; n1->right = n4; n2->left = n3; n2->right = NULL; n3->left = NULL; n3->right = n7; n4->left = n5; n4->right = n6; n5->left = NULL; n5->right = NULL; n6->left = NULL; n6->right = NULL; n7->left = NULL; n7->right = NULL; return n1; } //通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树 BTNode* BinaryTreeCreate2(char* a, int* pi)//这里的*pi是下标,如果不使用下标在特殊情况下*pi下标对应的值会被后面的值给覆盖了 { if (a[*pi] == '#')//如果数组里面的元素是#,那么下标*pi就加加,到下一位 { (*pi)++; return NULL; } BTNode* root = (BTNode*)malloc(sizeof(BTNode));//动态开辟root if (root == NULL) { perror("malloc fail\n"); exit(-1); } root->data = a[(*pi)++];//二叉树的节点值就等于数组a里面的元素 root->left = BinaryTreeCreate2(a, pi);//左子树递归 root->right = BinaryTreeCreate2(a, pi);//右子树递归 return root;//返回root就是返回我们构建出来的二叉树的起始地址 } // 二叉树销毁 void BinaryTreeDestory(BTNode* root) { if (root == NULL) return; BinaryTreeDestory(root->left); BinaryTreeDestory(root->right); free(root); } // 二叉树节点个数 int BinaryTreeSize(BTNode* root) { return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; //如果root不等于NULL,那么就返回左子树节点与右子树节点加上1的和,就是整个二叉树节点个数 } // 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root) { if (root == NULL) return 0; if (root->left == NULL && root->right == NULL)//如果节点的左子树和右子树都为空,那么该节点就是叶子节点,返回1 return 1; return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);//左子树的叶子节点加上右子树的叶子节点 } //二叉树高度/层次 int BinaryTreeHeight(BTNode* root)//这里的函数是有返回值的,所以左右子树递归结果要用一个int变量进行统计 { if (root == NULL) return 0; int leftheight = BinaryTreeHeight(root->left);//如果这里没有leftheight和下面的rightheight就接收不到左右子树的返回结果 int rightheight = BinaryTreeHeight(root->right); return leftheight > rightheight ? leftheight + 1 : rightheight + 1; //因为是求树高,所以左右子树高度高的那一个加上根就是整个树的高度 } // 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k) { assert(k > 0); if (root == NULL) return 0; if (k == 1)//如果k等于1,就直接返回1,因为左右子树递归到第k层的时候有且仅有一个节点 return 1; //转换为求子树的k-1层 return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1); //左右递归,k依次减一,表示每次递归一层 } // 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, NDataType x)//与上面一样,函数有返回值的 { if (root == NULL) return NULL; if (root->data == x)//如果data等于x,直接返回root当前的地址 return root; BTNode* left = BinaryTreeFind(root->left, x);//这里和下面都需要一个BTNode指针类型来接收左右子树递归返回的地址 //if(left)//如果left不等于NULL,就返回left //return left; BTNode* right = BinaryTreeFind(root->right, x); //if(right)//如果right不等于NULL,就返回right //return right; //return NULL;//如果left和right都等于NULL,就返回NULL return left == NULL ? right : left; //这里是一个小妙招,如果left等于NULL,就返回right地址;即便是right是NULL,返回right也没错,因为left是NULL } // 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } printf("%d ", root->data); BinaryTreePrevOrder(root->left); BinaryTreePrevOrder(root->right); } // 二叉树中序遍历 void BinaryTreeInOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } BinaryTreeInOrder(root->left); printf("%d ", root->data); BinaryTreeInOrder(root->right); } // 二叉树后序遍历 void BinaryTreePostOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } BinaryTreePostOrder(root->left); BinaryTreePostOrder(root->right); printf("%d ", root->data); } // 层序遍历 void BinaryTreeLevelOrder(BTNode* root)//使用队列最合适 { Queue p; QueueInit(&p); if (root)//如果树的节点不为空,就先把树的节点入进去 QueuePush(&p, root); while (!QueueEmpty(&p))//如果队列不为空 { BTNode* front = QueueFront(&p);//出队头数据 QueuePop(&p); printf("%d ", front->data);//打印 if (front->left)//上一层节点出的时候,带下一层左节点 QueuePush(&p, front->left); if (front->right)//上一层节点出的时候,带下一层右节点 QueuePush(&p, front->right); } printf("\n"); QueueDestroy(&p); } // 判断二叉树是否是完全二叉树(使用层序遍历方法) int BinaryTreeComplete(BTNode* root) {//与上面一样,上一层节点出的时候带下一层节点,当出的节点为NULL时,后面数据必须都为NULL,否则就是错的 Queue p; QueueInit(&p); if (root)//如果树的节点不为空,就先把树的节点入进去 QueuePush(&p, root); while (!QueueEmpty(&p)) { BTNode* front = QueueFront(&p); QueuePop(&p); if (front == NULL)//当出到NULL的时候就跳出 break; QueuePush(&p, front->left); QueuePush(&p, front->right); } while (!QueueEmpty(&p))//到这里如果后面全是NULL,那么是完全二叉树 { BTNode* front = QueueFront(&p); QueuePop(&p); if (front != NULL) { QueueDestroy(&p);//记得销毁 return false;//如果后面有一个数据不是NULL,那么就不是完全二叉树 } } QueueDestroy(&p); return true; } int main() { BTNode* root = BinaryTreeCreate1(); BinaryTreePrevOrder(root);//前序遍历 printf("\n"); BinaryTreeInOrder(root);//中序遍历 printf("\n"); BinaryTreePostOrder(root);//后序遍历 printf("\n"); printf("二叉树结点个数:%d\n", BinaryTreeSize(root)); printf("二叉树叶子结点个数:%d\n", BinaryTreeLeafSize(root)); printf("二叉树的高度:%d\n", BinaryTreeHeight(root)); printf("节点%d的地址为:%p\n", 5, BinaryTreeFind(root, 5)); BinaryTreeFind(root, 5)->data *= 10;//修改 BinaryTreePrevOrder(root);//前序遍历 printf("\n"); //char a[18] = "ABD##E#H##CF##G##"; //int pi = 0; BTNode* root = BinaryTreeCreate2(a, &pi); //root = BinaryTreeCreate2(a, &pi); //BinaryTreePrevOrder(root);//要用%c遍历 BinaryTreeLevelOrder(root);//层序遍历 printf("该二叉树是不是完全二叉树:%d\n", BinaryTreeComplete(root));//0表示不是完全二叉树,1表示是完全二叉树 BinaryTreeDestory(root);//二叉树的销毁 //BinaryTreeDestory(&root); root = NULL; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
总结
到目前为止,我们有关二叉树的知识基础的全部讲完了!剩下二插树的知识等到c++内容再讲解更简单一些。下一期就进入我们初阶数据结构的最后一个大纲了——排序,大家一起加油!
-
相关阅读:
古代汉语(王力版)笔记 通论8-9
Linux eBPF介绍(二)
前端环境变量释义import.meta.env.xxx
clickhouse--join操作汇总【semi、anti、any、asof、global、colocate、cross】
vue中的常用指令
不是跨域访问权限_而是后台代码错误_错误一点点排
[基础库Numpy] 技能树总结:一篇文章学会Numpy库
数据库连接性比较:Navicat 和基于 Java 的工具
课本在servlet中检索参数并验证,最后向用户发送验证消息
Pyppeteer中文文档
- 原文地址:https://blog.csdn.net/kdjjdjdjjejje128/article/details/126527752
