大纲

1.流网络&最大流
2.Edmonds-Karp算法求解
3.Dinic算法求解
4.最大流求二分图匹配

1.流网络&最大流

流网络简介

流网络G(V, E)是一个有向图，图中每条边(u, v)∈E都有一个非负权值c(u, v) ，称为边的容量。并
且，如果边集E包含一条边(u, v)，则图中不存在反方向的边(v, u)。如果(u, v)∉ E，则c(u, v) = 0。
在流网络的所有节点中，有两个特殊节点：源点S和汇点T。

流网络示例：

设G(V, E)是一个流网络，其容量函数为c，设S为网络的源点，T为网络的汇点。G中的流是一个实数函数f(u, v) (u∈V && v属于V)且满足以下性质：

① 容量限制：对于任意节点u, v∈V，要求：0 ≤ f(u, v) ≤ c(u, v)。
② 流量守恒：对于任意节点u∈V - {S,
T}，要求：所有x∈Vf(x, u) = 所有y∈Vf(y, u)
③ 斜对称：f(u, v) = - f(v, u)

实例

例如下图的网络流量为5（流量/容量）。

对于一个给定的网络，合法的流函数f有很多，其中使得整个网络的流量最大的流函数被称为网络的最大流，此时的流量被称为网络的最大流量。

例如：下图的流网络的最大流量为6（流量/容量）。

概念：

残留网络（残量网络）：任意时刻，网络中所有节点以及剩余容量大于0的边构成的子图称为残留网络。

初始化：基于原始网络建立残存网络，初始化时残留网络和原网络一致。

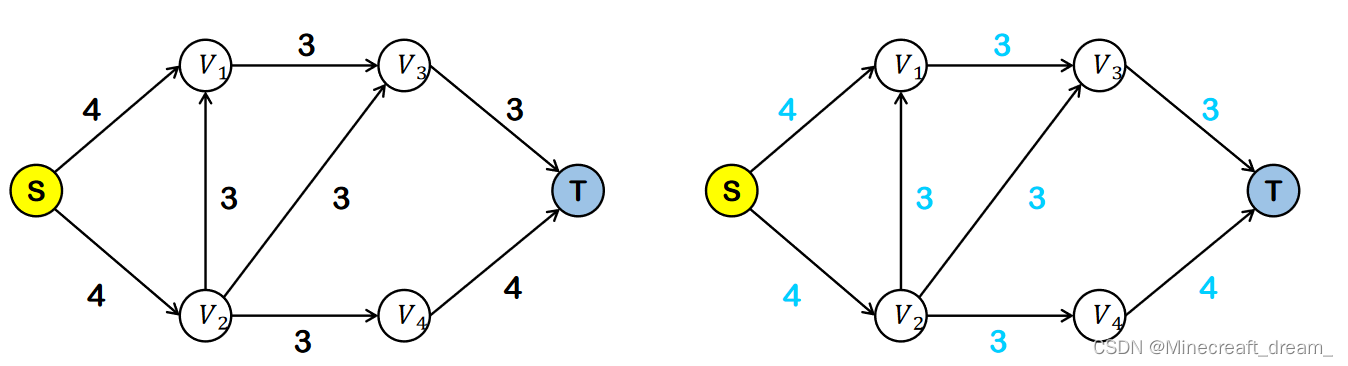
暴力求解最大流

第1步：从残存网络中找出一条从起点S到终点T的简单路径。
第2步：基于路径中容量最小的边，更新残留网络。

第3步：从残留网络中删除已经饱和的边。
重复上述3步操作，直到图中不存在S->T的路径。
流量 = 容量 - 空闲量

算法问题：上面描述的简单算法不能确保一定可以找到最大流。
简单算法计算出的流为阻塞流，最大流也是阻塞流的一种。

2.Edmonds-Karp算法求解

(1).Ford-Fulkerson算法

简单算法不会反悔，一旦被选中就不会再改变，Ford-Fulkerson是在简单算法上的一种改进算法，可以确保找到最大流。

初始化：基于原始网络建立残留网络，初始化时残留网络和原网络一致。
第1步：从残存网络中找出一条从起点S到终点T的简单路径。
第2步：基于路径中容量最小的边，更新残留网络。
第3步：从残留网络中删除已饱和的边。
第4步：添加一条反向路径，路径中边的容量 = 原路径的流量。

重复上述4步操作，直到图中不存在S->T的路径

反向路径使得流量可以反悔回流。

合并方向相同的边，不存在S->T的路径后删除反向路径。

流量 = 容量 - 空闲量

流量 = 容量 - 空闲量，最大流量 = 2 + 4 = 6。

算法缺陷：Ford-Fulkerson算法在极端情况下时间复杂度非常糟糕。

Ford-Fulkerson最坏情况下的重复次数等于最大流的大小。
设图中边的数量为M，单次查找路径的时间复杂度为O(M)
设流网络的最大流为F，则Ford-Fulkerson时间复杂度为O(F * M)。

2.Edmonds-Karp算法

2.1Edmonds-Karp算法流程

Edmonds-Karp算法是Ford-Fulkerson算法的性能优化算法，时间复杂度不依赖最大流的大小。

Edmonds-Karp算法每次找的路径都是S->T的最短路径，寻找最短路时将图当做无权图。
Ford-Fulkerson算法允许用任何的方式寻找S->T的路径，所以可以将Edmonds-Karp算法
看成Ford-Fulkerson算法的一种实现方式。 Edmonds-Karp算法的时间复杂度为𝐀(𝐀2 ∗
𝐀)，其中N和M分别为图中顶点数和边数。 ① 原网络中有M条边，残留网络中最多有2M条边，找最短路径的时间复杂度为O(M)。 ②
Edmonds和Karp证明了最坏情况下算法循会环M*N次。

1. 构建残留网络，初始化的残留网络就是原网络的一个拷贝。
2. 重复以下操作，直到残留网络中不存在增广路：（一条从S到T的路径，边上剩余流量都>0） ① 在残留网络中找最短增广路。 ② 计算增广路中各边上的剩余流量的最小值minf。 ③ 更新残留网络，将增广路中的每条边的剩余容量 - minf。 ④
   增加反向路径，将增广路的反向路径中各边的剩余容量 + minf。

Edmonds-Karp算法流程代码实现

核心部分：

3.Dinic算法求解

(0).Dinic算法历史

话说Dinic算法应该叫做Dinitz算法，接下来我把这一段有趣的历史简单的说一下。

Dinic算法由Yefim Dinitz发表于1970年，早于Edmonds-Karp发表的1972年。由于Dinic算法
发表于苏联，Edmonds和Karp在发表Edmonds-Karp算法时，并不知道Dinic算法的存在。
Even和Tarjan发表于1975年的论文，首次将Dinitz的算法介绍给西方。
Even和Tarjan错误的将Dinitz的名字写成了Dinic，从此该算法就被称为Dinic算法了。
Dinic算法时间复杂度是O(M * N^2)，优于Edmonds-Karp算法的O(N * M^2)。

(1).进入正题,Dinic算法

通俗的说，有了这些流量就不能再有其他流量，也就是说这些流量阻塞了管道。

分层图：对图进行BFS，设d[x]表示顶点x到起点s的最小距离，在残留网络中满足d[v] = d[u] +1的边(u, v)构成的子图称为分层图。

1. 构建残留网络（剩余流量），初始化的残留网络就是原网络的一个拷贝。
2. 重复以下操作，直到残留网络中不存在增广路：
   ① 构建残留网络的分层图（BFS）。
   ② 在分层图中寻找阻塞流（普通算法dfs）
   ③ 使用阻塞流更新残留网络（残留网络中的剩余流量 - 阻塞流中的流量），增加反向路径。

Dinic算法实践示例：

10步详细过程。

1.建立残留网络的分层图

2.在分层图中找阻塞流

3.使用阻塞流更新残留网络

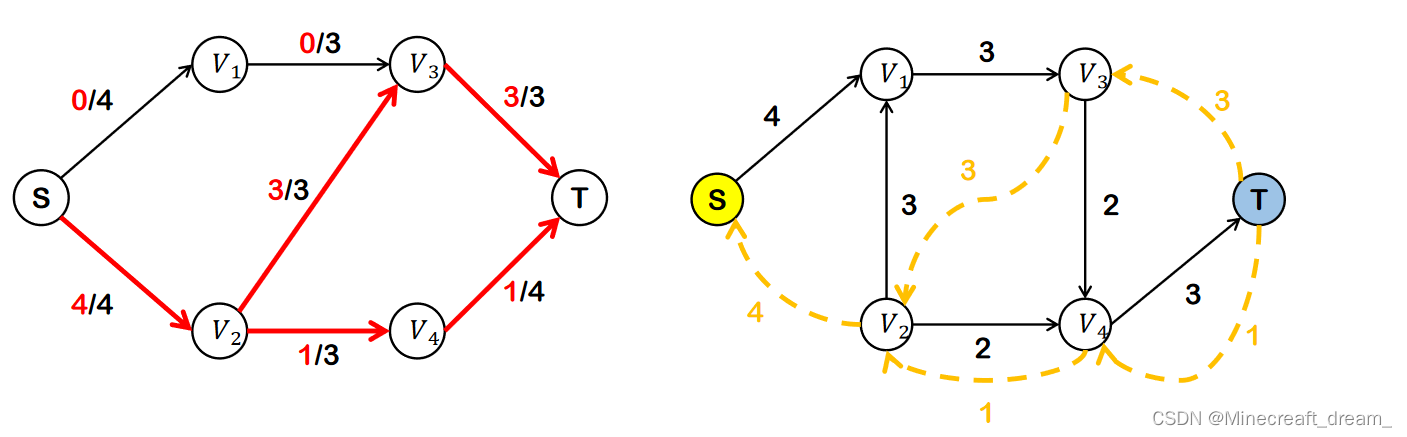
4.建立残留网络的分层图

5.在分层图中找阻塞流

6.使用阻塞流更新残留网络

7.建立残留网络的分层图

8.在分层图中找阻塞流

9.使用阻塞流更新残留网络

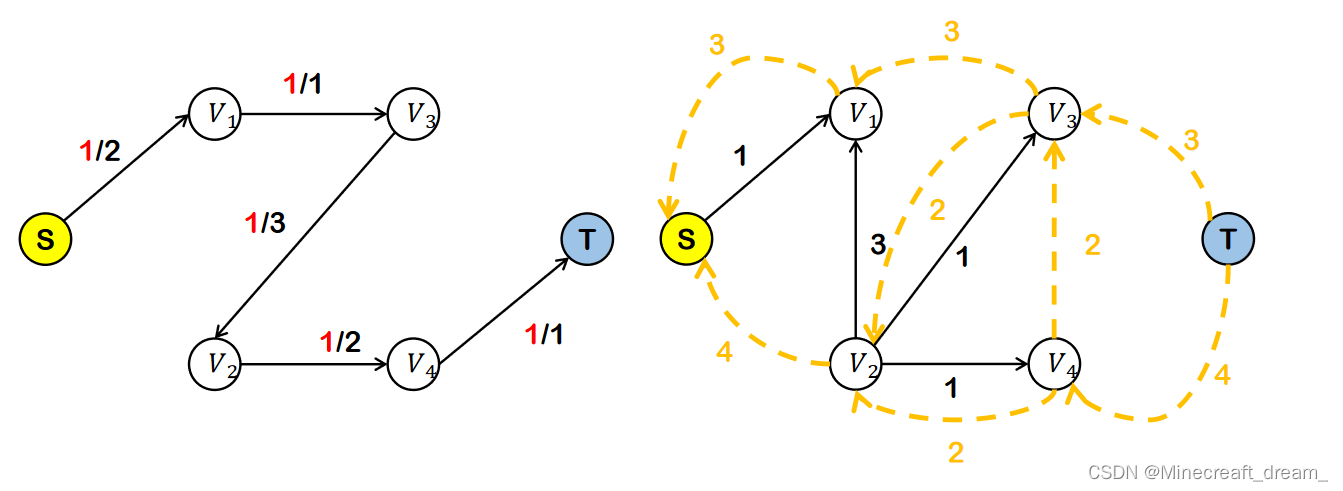
10.不存在增广路了，将反向边去掉，最大流 = 容量 - 空闲量 = 算法过程中阻塞流之和。

Dinic算法代码实现：

核心部分：

4.最大流求解二分图匹配

可以将二分图最大匹配转换为最大流问题，Dinic算法求解二分图最大匹配时间复杂度：O(M sqrt (N))

① 建立超级源点S和超级终点T，建立S到每个左部节点的有向边，权值为1，建立每个右部节 点到T的有向边，权值为1。 ②
原图中的无向边改为从左部到右部的有向边，权值为1，最大匹配问题转换为S->T的最大流。 ③
最大流经过的原图中的点和边，就是最大匹配的匹配点和匹配边。

概念：

完备匹配：给定一个二分图，其左部右部节点数相同，都为N。如果该二分图的最大匹配包含N
条匹配边，则称该二分图具有完备匹配。
多重匹配：给定一张包含N个左部节点、M个右部节点，从中选出尽量多的边，使第i个左部节点
至多与L[i]条选出的边相连，第i个右部节点至多与R[i]条选出的边相连。该问题称为二分图的多
重匹配。

多重匹配问题可以转换为最大流问题进行求解：

① 建立超级源点S和超级终点T，建立S到每个左部节点的有向边，权值为L[i]，建立每个右部 节点到T的有向边，权值为R[i]。 ②
原图中的无向边改为从左部到右部的有向边，权值为1，最大匹配问题转换为S->T的最大流。