算法入门——堆排序

目录

堆

堆的向下调整

构造堆

堆排序

---

在上篇文章学习了算法入门——插入排序、快速排序，这篇文章学习算法入门——堆排序。

堆

堆是一种特殊的完全二叉树结构，堆可以分为大根堆和小根堆，其中

• 大根堆：一棵完全二叉树，满足任一节点都比其子节点都大；

• 小根堆：一棵完全二叉树，满足任一节点都比其子节点都小；

如下图所示：

9比8大，8比6大，1比2小，2比3小。

堆的向下调整

当根节点的左右子树都是堆时，但根节点不满足堆的性质，如下图所示：

由于根节点为3且该堆为大根堆，不满足比其子节点都大，所以需要进行一次向下调整来把该二叉树变为堆。

向下调整过程如下：

首先把根节点3取出来，再对比左右子树的根节点大小，大的放在根节点中，如下图所示：

由于9比7大，所以9被放在根节点，那么原来存放9的位置就空了，接下来8与6对比，大的放在9原来的位置，如下图所示：

接下来2与4对比，4比2大，4就放在8原来的位置，最后把堆最初的根节点3放在4原来的位置上，如下图所示：

这样就成功把二叉树转变为堆了。

在上面最初的二叉树转换为列表：3,9,7,8,6,0,1,2,4,5，向下调整示例代码如下：

def sift(li, low, high):
    i = low      # i最开始指向根节点，也就是列表的第一个元素下标
    j = 2 * i + 1      # 左子树的节点开始
    tmp = li[low]             # 把堆顶元素保存，也就是保存列表的第一个元素
    while j <= high:          # 只要还有叶子节点
        if j + 1 <= high and li[j + 1] > li[j]:  # 如果有且右子树比较大
            j = j + 1          # 把左子树的节点与堆顶元素比较大小改为与右子树的节点比较大小
        if li[j] > tmp:    # 当堆顶元素小于子节点的元素时
            li[i] = li[j]   # 子节点元素放在节点位置
            # 比较下一层节点
            i = j
            j = 2 * i + 1
        else：
         li[i]=tmp   # 否则该堆顶元素该节点上
    else:
        li[i]=tmp       # 把tmp放在该节点上
    print(li)
li=[3,9,7,8,6,0,1,2,4,5]
sift(li,0,len(li)-1)

运行结果如下：

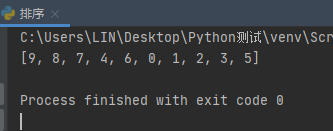
这样就把非堆转换为堆了。

构造堆

如何把如下图的二叉树转换为堆呢？

首先我们通过对比叶子节点和子节点大小，大的往上提，如下图所示：

5和4交互位置后，根据下图红框的顺序比较大小，大的移动到节点上，如下图所示：

最终得出的堆如图所示：

简单来说就是把每个节点与其叶子节点比较大小，通过向下调整的方法把节点与叶子节点位置交换。

示例代码如下：

def heap_sort(li):
    n=len(li)      # n为列表的长度
    for i in range((n-2)//2,-1,-1):   # 从列表后面开始遍历
        # i表示建堆的时候调整部分的根的下标
        sift(li,i,n-1)     # 调用刚才编写的向下调整函数 

这样就可以把一个二叉树转换为堆。

堆排序

我们成功把非堆的二叉树转换为堆，但堆转换的列表并不是排好序。

由于堆顶肯定是最大的元素，这时我们可以每次把堆顶提取出来，再把堆最后的叶子节点放在堆顶，通过堆的向下调整来调整堆元素，这时堆顶又变为了堆中最大的元素，再提取堆顶，这样反复就可以把堆排好序了。如下图所示：

首先把堆顶元素提取出来，再把最后面的叶子节点放在堆顶，如下图所示：

通过向下取整把该二叉树变为堆，再通过刚才的步骤提取堆顶，这样方法就可以把列表排好序。

示例代码如下：

def last(li):
    n=len(li)
    for i in range(n - 1, -1, -1): # 从列表后面开始遍历
        # i指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i - 1)      # i-1是最新的叶子节点
    print(li)

堆排序完整代码如下：

# 堆的向下调整
def sift(li, low, high):
    i = low      # i最开始指向根节点，也就是列表的第一个元素下标
    j = 2 * i + 1      # 左子树的节点开始
    tmp = li[low]             # 把堆顶元素保存，也就是保存列表的第一个元素
    while j <= high:          # 只要还有叶子节点
        if j + 1 <= high and li[j + 1] > li[j]:  # 如果有且右子树比较大
            j = j + 1          # 把左子树的节点与堆顶元素比较大小改为与右子树的节点比较大小
        if li[j] > tmp:    # 当堆顶元素小于子节点的元素时
            li[i] = li[j]   # 子节点元素放在节点位置
            # 比较下一层节点
            i = j
            j = 2 * i + 1
        else：
         li[i]=tmp   # 否则该堆顶元素该节点上
    else:
        li[i]=tmp       # 把tmp放在该节点上
    return li
 
# 构建堆
def structure_heap(li):
    n = len(li)
    for i in range((n - 2) // 2, -1, -1):
        # i表示建堆的时候调整部分的根的下标
        sift(li, i, n - 1)
    print('构造的堆：',li)
    heap_last(li)
 
# 堆排序
def heap_last(li):
    n=len(li)
    for i in range(n - 1, -1, -1):
        # i指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i - 1)      # i-1是新的high
    print('堆排序后:',li)
 
li=[2,4,5,1,9,8,6,7,3,0]
print('原始列表:',li)
structure_heap(li)

运行结果如下图：

堆排序的时间复杂度为：O(nlogn)。

好了，关于算法入门——堆排序就学到这里了，下篇文章学习算法入门——归并排序、希尔排序。

公众号：白巧克力LIN

该公众号发布Python、数据库、Linux、Flask、自动化测试、Git、算法等相关文章！

- END -