-
换根DP总结
洛谷P3478

先来看一道例题,很经典的一道换根DP题。考虑暴力,依次枚举以每一个点为根的深度之和,复杂度是
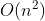 ,不能通过此题。这时就需要用换根DP把复杂度降为
,不能通过此题。这时就需要用换根DP把复杂度降为 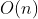 。
。我们先进行一次
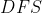 ,假设以
,假设以 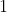 为根,把深度之和求出来。
为根,把深度之和求出来。第二次
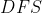 是换根DP的关键。考虑根节点由
是换根DP的关键。考虑根节点由 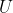 变成
变成  ,那么
,那么 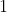 号节点和
号节点和 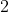 号节点的深度要减一,
号节点的深度要减一,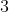 号节点的深度要加一。也就是说,
号节点的深度要加一。也就是说, 子树内的节点深度都要减一,其余的节点深度都要加一。
子树内的节点深度都要减一,其余的节点深度都要加一。于是有转移式
![f[v] = f[u] - size[v] + (sum - size[v])](https://1000bd.com/contentImg/2022/08/18/034735202.gif) ,即
,即![f[v] = f[u] + sum - 2*size[v]](https://1000bd.com/contentImg/2022/08/18/034736291.gif) 。
。
一定要注意,先把以
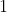 号节点为根的总深度求出来,即先求出
号节点为根的总深度求出来,即先求出 ![f[1]](https://1000bd.com/contentImg/2022/08/18/034737330.gif) ,才能进行往后的转移。
,才能进行往后的转移。- #include
- #define re register
- #define int long long
- using namespace std;
- inline int read(){
- int x=0,f=1;char ch=getchar();
- while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
- while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
- return x*f;
- }
- const int M = 2e6+10;
- int n;
- int head[M],siz[M],dep[M],f[M];
- int cnt,ans,pos;
- struct edge{
- int to,nxt;
- }e[M];
- void add(int u,int v){
- e[++cnt].to = v;
- e[cnt].nxt = head[u];
- head[u] = cnt;
- }
- void dfs(int u,int fa){
- siz[u]=1;
- dep[u]=dep[fa]+1;
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- dfs(v,u);
- siz[u]+=siz[v];
- }
- }
- void dfs2(int u,int fa){
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- f[v] = f[u]+n-2*siz[v];
- dfs2(v,u);
- }
- }
- signed main(){
- n=read();
- for(re int i(1) ; iint u=read(),v=read();add(u,v),add(v,u);}dfs(1,0);for(re int i(1) ; i<=n ; ++i) f[1]+=dep[i];dfs2(1,0);for(re int i(1) ; i<=n ; ++i) if(ansprintf("%d",pos);return 0;}
洛谷P2986
和上一道题不同的是,每一个点有一个点权,而且每一条边有一条边权。但换根DP的做法是类似的。先以
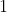 为根节点进行一次
为根节点进行一次 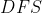 ,把每一个点的子树大小求出来,记为
,把每一个点的子树大小求出来,记为 ![size[i]](https://1000bd.com/contentImg/2022/08/18/034738163.gif) 。同时把
。同时把  号节点的答案处理出来。
号节点的答案处理出来。
考虑如何处理
 号节点的答案。
号节点的答案。 子树的点的数量
子树的点的数量 
 +
+ ![f[v]](https://1000bd.com/contentImg/2022/08/18/034741206.gif) 和
和 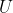 子树的点的数量
子树的点的数量  +
+ ![f[u]](https://1000bd.com/contentImg/2022/08/18/034742950.gif) 。也就是对于
。也就是对于 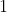 号点的所有子树都进行如此操作。
号点的所有子树都进行如此操作。![f[u] += f[v]+size[v]*e[i].w](https://1000bd.com/contentImg/2022/08/18/034743830.gif) ,在
,在 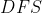 的时候往上更新即可。
的时候往上更新即可。然后来看第二个
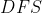 。同样,从
。同样,从 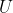 转移到
转移到  有关系式
有关系式 ![f[v] = f[u] - size[v]*e[i].w + (sum-size[v])*e[i].w](https://1000bd.com/contentImg/2022/08/18/034744571.gif) ,所以进行转移即可。最后的答案就是
,所以进行转移即可。最后的答案就是 ![min(f[i])](https://1000bd.com/contentImg/2022/08/18/034745664.gif) 。
。- #include
- #include
- #include
- #include
- #include
- #define re register
- #define int long long
- #define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
- #define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
- using namespace std;
- inline int read(){
- int x=0,f=1;char ch=getchar();
- while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
- while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
- return x*f;
- }
- const int M = 2e5+10;
- int head[M],a[M],siz[M],f[M];
- int n;
- int cnt,ans=1e15,sum;
- struct edge{
- int to,nxt,w;
- }e[M];
- inline void add(int u,int v,int w){
- e[++cnt].to = v;
- e[cnt].w = w;
- e[cnt].nxt = head[u];
- head[u] = cnt;
- }
- inline void dfs1(int u,int fa){
- siz[u] = a[u];
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- dfs1(v,u);
- siz[u] += siz[v];
- f[u] += f[v]+siz[v]*e[i].w;
- }
- }
- inline void dp(int u,int fa){
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- f[v] = f[u] - siz[v]*e[i].w + (sum-siz[v])*e[i].w;
- dp(v,u);
- }
- }
- signed main(){
- n=read();
- rep(i,1,n) a[i] = read(),sum += a[i];
- rep(i,1,n-1){
- int u=read(),v=read(),w=read();
- add(u,v,w),add(v,u,w);
- }
- dfs1(1,0);
- dp(1,0);
- rep(i,1,n) ans = min(ans,f[i]);
- printf("%lld\n",ans);
- return 0;
- }
CF1092F

和上面那道题基本上一样,把求最小改成求最大就完事了
- #include
- #include
- #include
- #include
- #include
- #define re register
- #define int long long
- #define rep(a,b,c) for(re int a(b) ; a<=c ; ++a)
- #define drep(a,b,c) for(re int a(b) ; a>=c ; --a)
- using namespace std;
- inline int read(){
- int x=0,f=1;char ch=getchar();
- while(ch<'0'||ch>'9'){if(ch == '-') f=-1 ; ch=getchar();}
- while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48) ; ch=getchar();}
- return x*f;
- }
- const int M = 4e5+10;
- int head[M],a[M],dep[M],siz[M],f[M];
- int cnt,sum;
- struct edge{
- int to,nxt;
- }e[M];
- inline void add(int u,int v){
- e[++cnt].to = v;
- e[cnt].nxt = head[u];
- head[u] = cnt;
- }
- int n;
- inline void dfs1(int u,int fa){
- siz[u] = a[u];
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- dep[v] = dep[u] + 1;
- dfs1(v,u);
- siz[u] += siz[v];
- f[u] += f[v] + siz[v];
- }
- }
- inline void dfs2(int u,int fa){
- for(re int i(head[u]) ; i ; i=e[i].nxt){
- int v = e[i].to;
- if(v == fa) continue;
- f[v] = f[u] - siz[v] + sum - siz[v];
- dfs2(v,u);
- }
- }
- signed main(){
- n=read();
- rep(i,1,n) a[i] = read(),sum += a[i];
- rep(i,1,n-1){
- int u=read(),v=read();
- add(u,v),add(v,u);
- }
- dfs1(1,0);
- dfs2(1,0);
- int ans = 0;
- rep(i,1,n) ans = max(ans,f[i]);
- printf("%lld\n",ans);
- return 0;
- }
-
相关阅读:
zKSync 2.0 新特征解析
【ARM Trace32(劳特巴赫) 使用介绍 3 - trace32 访问运行时的内存】
3步就能制作漫画头像的机器人,想拥有一个吗?
大学生数学建模题论文
git命令提交代码到远程仓库
Mac RabbitMq 安装
Spring Boot配置多个日志文件记录不同类日志示例
javaScript-事件循环-微任务-宏任务
软件工程导论——第三章——需求分析
Oracle 常用命令大全
- 原文地址:https://blog.csdn.net/glorious_dream/article/details/126341402
