NLC: Search Correlated Window Pairs on Long Time Series(VLDB2022)

目前，许多应用，如物联网和工业互联网，从传感器连续收集数据点，形成长时间序列。发现时间序列之间的相关性是许多时间序列挖掘问题的基本任务。然而，现有的工作要么局限于检测关系的类型，如仅检测线性相关关系，要么未处理复杂的时间关系，如未考虑非对齐窗口或可变窗口长度。本文提出了一种有效的方法——非线性相关搜索(NLC)，用于搜索两个长时间序列上的相关窗口对。首先，提出窗口收缩和窗口扩展两种策略，快速找到高质量的相关窗口对候选;然后，通过嵌套一维搜索方法对候选集进行优化;进行了系统的实证研究，验证了所提出方法在合成和真实数据集上的效率和有效性。

阅读者总结：这篇论文在检索长时间序列最大信息熵窗口对问题上，主要创新：1）提出了这个问题，应该说，整篇论文的最大亮点在于问题本身。文中设计的算法不算很新颖，简单说就是find-refine两个过程。2）文中另一方面 是在分析这个问题上，采用数据驱动的方式，很有说服力，使阅读者相信这个问题值得采用新办法解决，同时在写作和文章布局上值得学习。

3）这篇论文和ICDE 2022上对齐窗口索引压缩问题，有类似的背景。但是ICDE上考虑的时间窗口对齐，没有考虑窗口时间延迟。因此这篇论文其实可以借鉴ICDE上的方式，以查询索引的方法寻找相关延迟窗口对，自觉上来说，查询时间和效率肯定比当前采用放缩窗口的方法要高很多。

问题：

1）所有这些工作都旨在从长时间序列对中挖掘局部线性相关性。然而，在许多应用中，由于复杂的物理或化学机理，时间序列具有很强的非线性关系

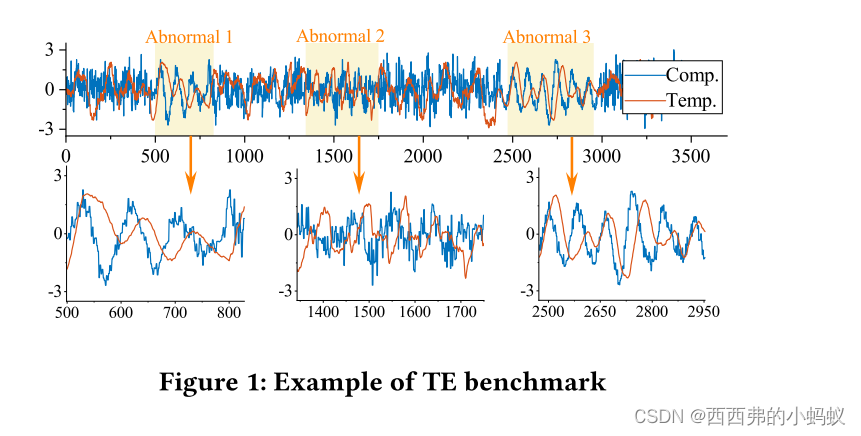 2）TYCOS有两个缺点。首先，在候选集生成阶段，只搜索对齐的相关窗口对;因此，对于时延较大的窗口对，算法的性能较差。其次，爬山法容易找到局部最优结果，而不是真正的最优结果。

 方法：

本文提出了一种两阶段的方法，非线性相关搜索(NLC)。在第一阶段，我们生成一组相关的候选窗口对。提出了窗口收缩和窗口扩展两种策略。窗口收缩策略适用于相关性的稀疏分布，具有较高的效率。它可以快速地修剪非限定区间。相比之下，窗口扩展策略速度稍慢，但当相关窗口分布更密集时，它可以发现更多的对。第二阶段将候选求精问题转化为一个优化问题，并采用一维嵌套搜索策略进行求解。

 

 

 

 

 MOTIVATION

如前所述，核心挑战是验证所有窗口对的巨大时间开销。由于每个时间窗口对由起始点、窗口长度和时间延迟3个因素决定，分析了这些因素对MI值的影响。

1）Starting Point and Window Length

 

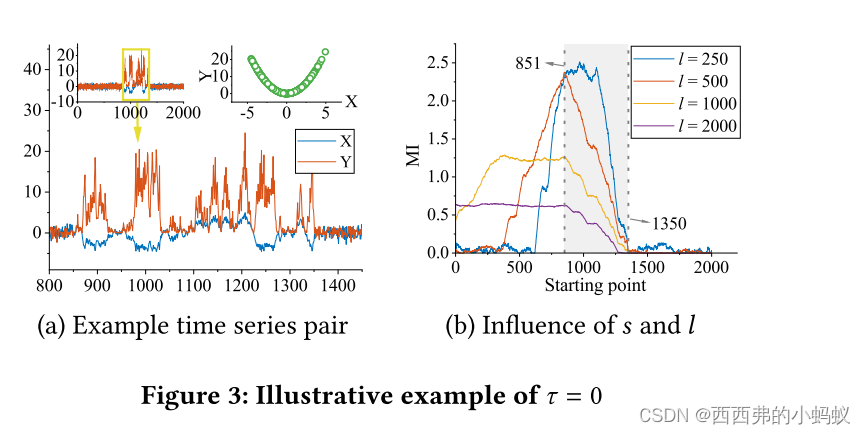
 2）Delay

 这个例子揭示了MI计算的一个属性。如果两个延时相等的窗口𝜏，𝑊1和𝑊2是相关的。然后两个延时较大的窗口𝜏，分别围绕𝑊1和𝑊2，也将相关。换句话说，我们生成的候选集具有模糊的起点和长度，但具有精确的时间延迟。支持我们选择的另一个原因是，与起始点和长度相比，随着时间延迟的变化，MI值的波动更快。

 Overview

 PHASE ONE: CANDIDATE GENERATION

为了生成候选集CP0，提出了窗口收缩和窗口扩展两种策略。前者首先找出可能包含合格相关数据对的大窗口对，并通过裁剪不相关部分来缩小窗口;相比之下，后者首先找到小窗口对，并将它们扩展到适当的长度。

1）Window Shrinking

 Window Extending

现在我们介绍第二种策略，窗口扩展。当相关对密集分布时，如果我们仍然使用大窗口，可能会出现在一个包络窗口中出现两个不同的相关对，由于我们在一个包络窗口中只保留了一个相关对，这将导致某些相关对被忽略。所以窗口扩展策略就是利用小窗口来寻找候选者。 

 PHASE TWO: WINDOWREFINEMENT

一般来说，DIRECT是一种基于采样的优化问题搜索策略。对于一个搜索空间上的目标函数，DIRECT通过迭代过程可以有效地找到全局最优解。DIRECT是一种三元搜索策略。其基本思想是将搜索空间划分为区间，通过采样和评估每个区间的中心点来选择下一步要搜索的矩形

 EXPERIMENTAL RESULTS