【双目视觉】 立体匹配算法原理之“代价空间与聚合、视差计算”

预备知识

1. 【双目视觉】 理想条件下计算物体距离_什么都只会一点的博客-CSDN博客
2. 【双目视觉】 立体匹配算法原理之“代价函数”_什么都只会一点的博客-CSDN博客

代价空间

$$C_{AD}(x,y,d)=\left|I_L(x,y)-I_R(x-d,y)\right|$$

d是移动像素的大小。以左图为基准。下面以左图的一个像素点P为例

1. d=0，右图不移动，计算$C_{AD0}$
2. d=1，右图向右移动一个像素点，再计算$C_{AD1}$
3. d=2，右图向右移动一个像素点，再计算$C_{AD2}$
4. …(d++，不断执行)…
5. 最后得到代价空间

代价聚合

🔥目的：对代价空间进行滤波，使边界平滑

Box Filtering（均值滤波）

$$C_d^A(p)=\frac{1}{N}\sum _q{C}_d(q)$$

N：窗口像素个数

效果：

Bilateral filter

Bilateral filter就是输入的代价，乘以一个高斯函数，实现平滑

效果：

Cross-based local stereo matching(自适应形状)

任意选取一个像素点，横向、纵向扩张，直到遇到颜色差异较大的地方才停下来。然后在扩张后的像素点，重复上述操作。这样，因为能及时发现边界，就能大概判断出一整块区域的视差图

🚀Semi-Global Matching

能量函数
E ( D ) = ∑ p ( C ( p , D p ) + ∑ q ∈ N p P 1   T [ ∣ D p − D q ∣ = 1 ] + ∑ q ∈ N p P 2   T [ ∣ D p − D q ∣ > 1 ] )

E(D)=​p∑​⎝ ⎛​C(p,Dp​)+q∈Np​∑​P1​ T[∣Dp​−Dq​∣=1]​+q∈Np​∑​P2​ T[∣Dp​−Dq​∣>1]⎠ ⎞​​

当$D_p-D_q=1$时，我们就取${\sum }_{\mathbf{q}\in N_{\mathbf{p}}}{P}_1\mathrm{T}\left[\left|D_{\mathbf{p}}-D_{\mathbf{q}}\right|=1\right]$

当$D_p-D_q>1$，我们就取${\sum }_{\mathbf{q}\in N_{\mathbf{p}}}{P}_2\mathrm{T}\left[\left|D_{\mathbf{p}}-D_{\mathbf{q}}\right|>1\right]$

优化步骤

1. 计算代价空间；(AD, BT, Census, MI, ….)

2. 代价聚合

   方向r上的路径代价
   L r ( p , d ) = C ( p , d ) + min ⁡ ( L r ( p − r , d ) L r ( p − r , d − 1 ) + P 1 L r ( p − r , d + 1 ) + P 1 min ⁡ i L r ( p − r , i ) + P 2 ) − min ⁡ k L r ( p − r , k )

   Lr(p,d)=C(p,d)+min(Lr(p−r,d)Lr(p−r,d−1)+P1Lr(p−r,d+1)+P1miniLr(p−r,i)+P2)−minkLr(p−r,k)" role="presentation" style="position: relative;">Lr(p,d)=C(p,d)+min(Lr(p−r,d)Lr(p−r,d−1)+P1Lr(p−r,d+1)+P1miniLr(p−r,i)+P2)−minkLr(p−r,k)$$\begin{array}{rl}{L}_{\mathbf{r}}(\mathbf{p},d)=& C(\mathbf{p},d)+min(L_{\mathbf{r}}(\mathbf{p}-\mathbf{r},d)\\ & L_{\mathbf{r}}(\mathbf{p}-\mathbf{r},d-1)+P_1\\ & L_{\mathbf{r}}(\mathbf{p}-\mathbf{r},d+1)+P_1\\ & \underset{i}{min}{L}_{\mathbf{r}}(\mathbf{p}-\mathbf{r},i)+P_2)-\underset{k}{min}{L}_{\mathbf{r}}(\mathbf{p}-\mathbf{r},k)\end{array}$$
   Lr​(p,d)=​C(p,d)+min(Lr​(p−r,d)Lr​(p−r,d−1)+P1​Lr​(p−r,d+1)+P1​imin​Lr​(p−r,i)+P2​)−kmin​Lr​(p−r,k)​
   当d=0时，$L_{\mathbf{r}}(\mathbf{p},d)=C(\mathbf{p},d)-{\min }_k{L}_{\mathbf{r}}(\mathbf{p}-\mathbf{r},k)$

   当|d|=1时，$L_{\mathbf{r}}(\mathbf{p},d)=C(\mathbf{p},d)+P_1-{\min }_k{L}_{\mathbf{r}}(\mathbf{p}-\mathbf{r},k)$

   当|d|=i时，$L_{\mathbf{r}}(\mathbf{p},d)=C(\mathbf{p},d)+P_2-{\min }_k{L}_{\mathbf{r}}(\mathbf{p}-\mathbf{r},k)$

   $L_r(p-r,d)$是该像素点左侧，最优代价。即当d=i时，左侧有最优代价，那么就$C(\mathbf{p},d)+P_2$

   各个方向的总聚合代价
   $$S(\mathbf{p},d)=\sum L_{\mathbf{r}}(\mathbf{p},d)$$
   例如opencv收录的sgbm算法，就是计算了下面5条路径的代价

   

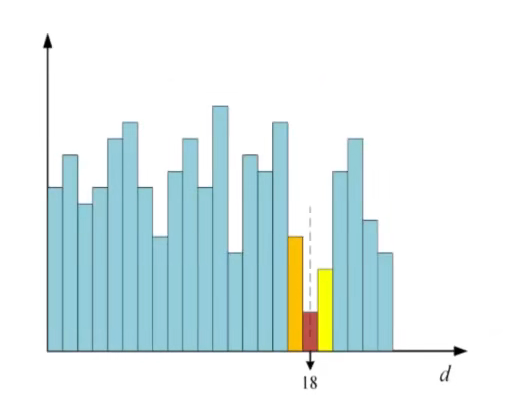
3. WTA

   Winner-Take-All,赢家通吃

   即我们发现在这条视差方向r上，纵轴（聚合后的代价）最小，那么我们就取出视差值（d=18）

   

4. 视差后处理