常见排序算法讲解（图解+代码+代码讲解）

前言： 本篇博客讲解排序算法，它的重要性不用说，无论是考研还是工作都需要会用。常见的排序有插入排序，选择排序，交换排序，归并排序。基于这四种排序的核心思想又延伸出各种排序。

• 详见如下图：
  

---

1，排序的基本概念与分类

1.1 排序的稳定性

在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，S1=S2，且S1在S2之前，而在排序后的序列中，S1仍在S2之前，则称这种排序算法是稳定的；否则称为不稳定的。

就是说，有两个相等的值，它俩在原数组的前后关系，再排完序之后，保持着以前的前后关系就称为排序稳定，如果前后位置关系发生变化就为排序不稳定。
比如：
原数组：

排序后数组：

两个数的前后位置关系不变，所以排序稳定，反之则不稳定。

1.2 内排序和外排序

内部排序是指待排的记录全部在内存中完成排序的过程，内部排序也称为内排序。若待排序记录的数量庞大，在排序的过程中需要使用到外部存储介质如磁盘等，这种涉及内外存储器数据交换的排序过程称为外部排序，又称为外排序。内排序是外排序的基础，外排序算法的原理和内排序算法的原理在很多方面都类似，但因内存的读写速度与外存的读写速度存在很大差别，因而实际操作中仍有不同。

总结一句话就是：全在内存中排序的是内排序，涉及到和外部储存器交换数据的为外排序。

---

2，排序算法

2.1 插入排序

插入排序的这种方法，其实生活中我们也会用到，比如打扑克牌时，我们整牌的时候，拿到牌插入我们整好的手牌里，摸一张整理一次，最终形成有序的手牌。插入排序的思想就是如此，将一个数据插入到一个有序的数据组内从而形成一个新的有序数据组。

2.1.1 直接插入排序

我们先来实现一个直接插入排序，拿到一个数组，它可能有序也可能是无序，上面说过，插入排序是将一个数据，插入到一个有序的数据组里，那么我们可以先排前两个数据，一个数肯定是有序的，第二个数插入到这一个数的左边或右边，依次往下，第三个往这俩个有序数组里插，依次循环，最终有序。

我们有了这样的思想，就该画图以及代码实现：
（1）一个数插入到一个有序数组中的实现
一， 将数字4插入到一个有序数组中，用一个end来指向最后一个数据的下标。

二 ，4比end指向的数据（6）小，所以6往后移一位，同时end向前走一位。

三，和上一步一样，4比5小，所以5往后移一位，end - -。

四，4比3大，所以end不动了，找到了4应该在的位置，把4插入此位置即可

（2）完成直接插入排序
知道了插入一个数据的过程，插入所有数据也不是难事了，不过就是加个循环。
代码实现如下：

void Inseart_sort(int* arry,int n)
{
	for (int i=0;i<n-1;i++)//控制循环end最后为n-2
	{
		int end = i;//从下标0，开始算有序,依次插入循环
		int x = arry[end + 1];//x保存要插入的数
		while (end >= 0)//end<0,也需退出循环
		{
			if (arry[end] > x)//比x大的往后挪
			{
				arry[end + 1] = arry[end];
				end--;
			}
			else
			{
				break;//从这里出去说明找到了x的位置
			}
		}
		arry[end + 1] = x;//end+1的位置放入x
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

代码讲解：
(1)比如要排这个数组的序；

(2)所以要调用函数，

(3)进入函数，并且走进循环，end=0，x=2（下标为end+1的数据，arry[1]）

(4)因为，arry[end]>x,所以进入if语句，数据往后挪动，arry[1]=arry[0],并且end减1。

(5)因为end=-1，不满足while的判断条件，退出while循环，然后end+1的位置放入x的值，也就是arry[0]=2;再回到for循环，i++，所以end=1，x=arry[2];

(6)因为x
(7)x<23,所以23向后挪动一位，end-1=1，x>4，所以break，然后再arry[2]=5;
就是这样一步一步的插入，通过上面的讲解后面的操作也如出一辙，大家肯定是懂了。最后排序完成，运行一下看看结果。

（3）直接插入排序总结
直接插入排序的核心思想就是，在一个有序数列中插入一个数，通过有序数列的挪动，最终找到此数的合适位置，然后一插入。
时间复杂度：O(n²)

2.1.2 希尔排序

希尔排序也是用的插入排序的思想，但是希尔排序是直接插入排序的优化版，它更快。直接插入排序在其基本有序的情况下，效率是较高的，只需要少量的插入操作就能完成排序。那么我们可不可以将一个数据组先进行预排序，使其基本有序（大的基本在后，小的基本在前），再进行直接插入排序，那么其效率也就得到提高。

预排序：使得数组基本有序，我们可以将数组中的数据分组去插入排序，分组也是有办法的，可以间隔3个的为一组，也可以间隔为2个的为一组，如果间隔为0的为一组，那么就是对全体进行直接插入排序。
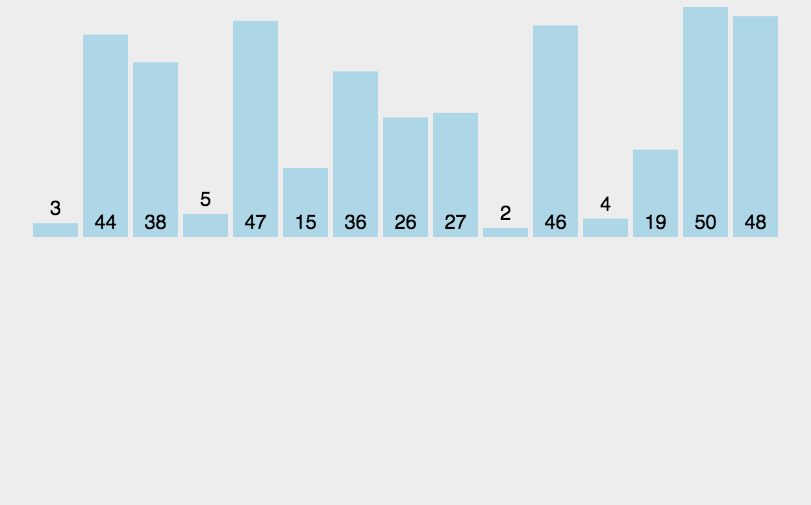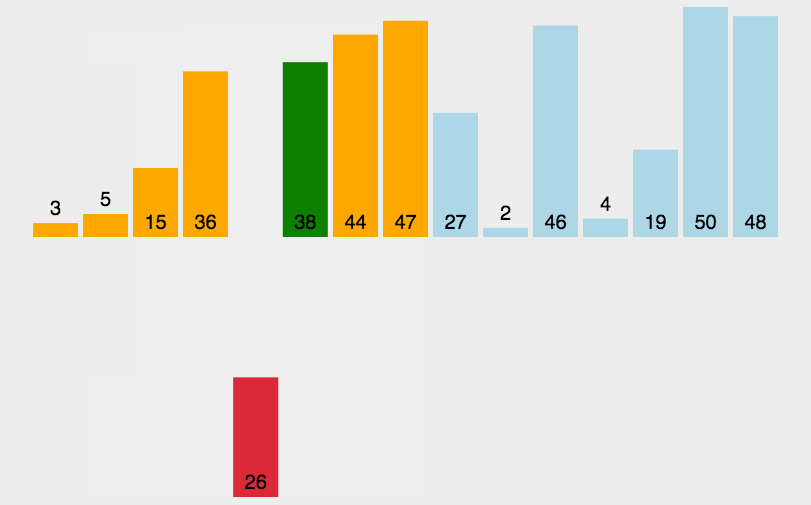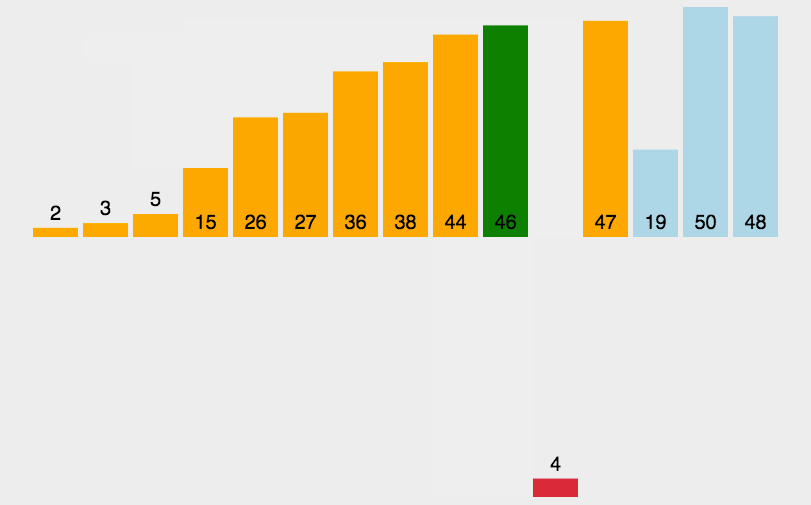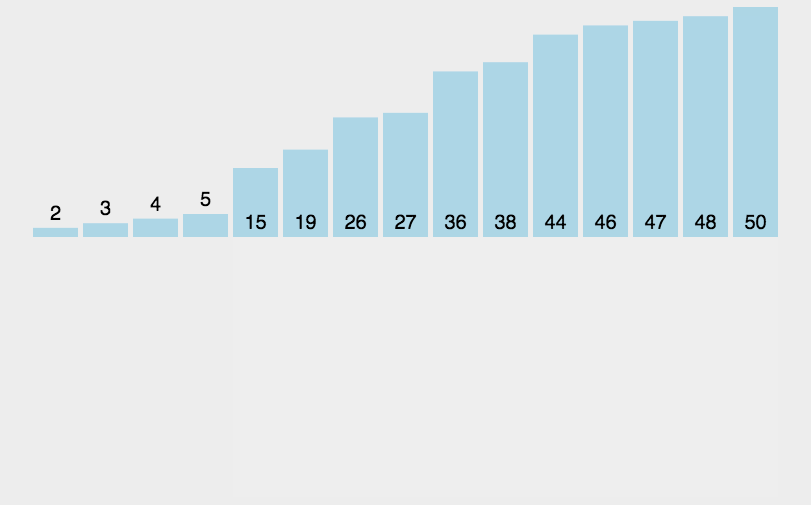
（1） 接下来我们用图来感受一下希尔排序的魅力。
对这个数组进行希尔排序，

我们先隔2个（从它开始数的第3个数）为一组，用相同颜色串联一起的为一组，

预排序结果如下：可以看到，预排序一次，比最初有序了一些，每次预排序，都朝着有序迈进一步，

我们再次预排序，使得间隔为1（从它开始数的第2个数）的为一组，分组如下：

再次对每组进行排序，可得如下结果：

可以看到这次预排序之后，更加有序了，接下来就是最后一步，对这个基本有序的数组进行直接插入排序，也就是间隔为0的为一组（从它开始数的第一个数），进行预排序，
所以结果如下：

通过以上的图解，大家可能更清晰的了解到了希尔排序，通过不断的预排序，最终得到有序的数组。
(2) 代码实现以及讲解

void Shell_sort(int* arry,int n)
{
	int gap = n;//gap是间隔加1，也就上面从它开始数的第几个数为一组
	while (gap > 1)//gap==1时，就是直接插入排序
	{
		gap = gap / 3 + 1;//这个 +1 是为了防止gap==0
		//对应上面的直接插入排序，gap==1就是直接插入排序，除了一个gap不同其余都一样
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int x = arry[end + gap];
			while (end >= 0)
			{
				if (arry[end] > x)
				{
					arry[end + gap] = arry[end];
					end-=gap;
				}
				else
				{
					break;
				}
			}
			arry[end + gap] = x;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

代码讲解：
从代码分析，可以看到，希尔排序就是直接插入排序的优化版，我们只需要控制一个gap，使gap
不断接近1，gap==1时就是直接插入排序，gap>1时，就是在不断的预排序使得数组接近有序。我们知道直接插入排序对于排基本有序的数组，效率是较高的。
(3) 希尔排序算法总结
希尔排序的出现使得排序算法的时间复杂度突破O(n²),从而达到O（n^1.3)。

---

2.2 选择排序

选择排序的逻辑：选择最小的和最左边的交换，然后选择次小的再和次左的交换，不断选择，交换最终使得数据组有序。这方法听起来有点笨笨的，就是选择最小的放在最左边（默认升序）。

2.2.1 直接选择排序

直接选择排序就是最基本逻辑的实现，我们直接结合代码和图去理解一下。

void Select_sort(int* arry, int n)
{
	for (int i = 0; i < n; i++)
	{
		int min = i;
		for (int j = i + 1; j < n; j++)//此循环用于找出最小的下标并且记录
		{
			if (arry[min] > arry[j]) 
			{
				min = j;
			}
		}//出了这个循环min指向最小数的下标
		//把最小的数和最左边的数交换
		int tmp = arry[i];
		arry[i] = arry[min];
		arry[min] = tmp;;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

（1）假如排序下图的数组，i为最左边下标，min=i，j=i+1，

（2）经过里面一层for循环后，min指向了3的位置，

（3）交换min和i的值，

（4）因为i
（5）和上一次一样，选出最小值4，和i处的值一交换。

就是这样，想必大家看到这也就明白了这个选择排序的逻辑。当i走到末尾，也就完成了排序。

2.2.2 直接选择排序优化版

还是直接选择排序，每次都选一个最小的数，是不是有点慢？所以我们想要优化一下它，自然而然的想到，可不可以一趟选俩个数，选出个最大值放在最右边，选出个最小值放在最左边边。
上一次选出一个数，用i来控制边界，如果选出两个数，我们也需要一个变量来控制右边界。就这样不断的选择，当左边界和右边界走到一起了，说明这个数据组就有序了。

代码实现：

void Select_sort2(int* arry, int n)
{
	int begin = 0;//左边界
	int end = n - 1;//右边界
	while (begin < end)
	{
		int max = begin; int min = begin;//都从左边开始找最大和最小
		for (int i = begin+1; i < end; i++)
		{
			if (arry[i] > arry[max])
				max = i;
			if (arry[i] < arry[min])
				min = i;
		}
		//把最小放在左边
		int tmp = arry[begin];
		arry[begin] = arry[min];
		arry[min] = tmp;
        //修正一下max的位置，这里不懂下面会讲到
		if (begin == max)
			max = min;
       //把最大放在右边
		tmp = arry[end];
		arry[end] = arry[max];
		arry[max] = tmp;
		//调整边界
		end--;
		begin++;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

上面有一个修正max位置，大家可能有点不懂，我来画图讲解一下。

走出循环后max和min分别指向了最大值和最小值的下标，我们可以看到这种情况下max和begin是相等的。
然后交换min和begin的值，就会导致max的值也被交换走了，交换到了min的位置，所以我们要对max的值重新调整一下，max=min。
（1）可以看到，交换了min和begin，把max的值交换到min的位置

（2）修正max的值，使max＝min

2.2.3 堆排序

走到堆排序这里，堆排序也是选择排序的思想，它比直接选择排序优化的地方在于，如何选出最小值。直接选择排序选择最小值用的是for循环去遍历数组；而堆排序选出最小用的是建堆的方式。建堆的时间复杂度为O(logn)比遍历数组的时间复杂度O(n)快了不少。我们知道大堆的堆顶是最大值，小堆的堆顶是最小值。升序我们建立的是大堆，降序我们是建立小堆，通过画图我们来理解推排序。堆是利用二叉树此数据结构，不懂的童鞋可以看我的博客二叉树知识概览，简单说一下堆这个东东，它就是一种二叉树结构，大堆：父亲结点大于子节点，根结点最大。小堆反之。

(1)图解堆排序
(1)下图是一个大堆，根节点为最大值。

(2)物理结构是一个数组，层序的排列。

(3)我们建立一个大堆是为了排 升序，所以可以用如下的办法，


(4)再重新建堆，但不能包括最后一个数，它是最大值相当于排好了，排在了末尾。

(5)可以看到通过重新建堆，堆顶又选出了剩余数组中最大值80，还是老办法。


(6)可以看到通过两次交换，建堆，数组的后两位已经排好了。就是这样的过程，堆排序。我就不完全画完了，接下来我们讲解代码来了解建堆以及排序的过程。
(2) 堆排序代码讲解

//交换数据的函数
void Swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}
//向下调整建堆用的函数
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//默认选左孩子
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		// 如果孩子大于父亲，则交换，并继续向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void Heap_Sort(int* a, int n)
{
    //建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//i是父亲的下标，从最后的叶子节点的父亲开始调
	{
		AdjustDown(a, n, i);
	}
	// 依次选数，调堆
	for (int end = n - 1; end > 0; --end)
	{
		Swap(&a[end], &a[0]);//交换头，尾位置

		// 再调堆，选出次小的数
		AdjustDown(a, end, 0);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

我们来分析代码，Swap函数是一个交换数据的函数，比较简单，这里就不讲了。
AdjustDown函数还是讲一下，这就是我们建堆用的函数。
建堆，我们可以用分治的思想 想，左子树，右子树都是大堆，再从根结点往下调整就是一个大堆了，这里大家可能会吐槽：你听听你在说什么? 我们来画图看一看吧还是。

(1)如下数组，我们来建成一个大堆。


(2)从最后一个叶子结点的父亲结点开始向下调整，也就是10结点，父亲结点的下标=(孩子节点的下标-1)/2。 所以10节点的位置就是（n-1-1）/2;可以看到数值大的孩子节点6<父亲节点10；所以不用调整。然后父亲节点减一就到了另一个父亲节点的位置，这里可以看上面的数组，所以到了根节点位置；为什么不管11节点呢？因为从最后一个叶子节点的父亲节点往下调整。可以看到根节点8的孩子是10和11；11>10,所以11和8的位置交换。

(3)然后因为child>n,所以退出while循环。
可以看到这个大堆已经建好了，我们可以结合一下，调用AdjusDown()函数时的代码。

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//默认选左孩子
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		// 如果孩子大于父亲，则交换，并继续向下调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
int main()
{
  for (int i = (n - 1 - 1) / 2; i >= 0; --i)//i是父亲的下标，从最后的叶子节点的父亲开始调
	{
		AdjustDown(a, n, i);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

大家想必有了想法，拿上图举例，n=5，i=1也就是10节点的小标，向下调整好后，i- -，i=0也就是根节点的位置，再向下调整，最终建成大堆。
然后我们来分析一下Heap_Sort函数，一进来就将数组建成大堆，然后对这个大堆，不断进行选数，调堆，最终完成排序。思想在上面已经讲过，此处不重复。
(3)堆排序算法分析
堆排序已经比较优了，时间复杂度O(n*logⁿ)，它就是优化在了选择最小数（或者最大数）
，用建堆，调堆的方式比直接遍历优化了不少。

---

2.3 交换排序

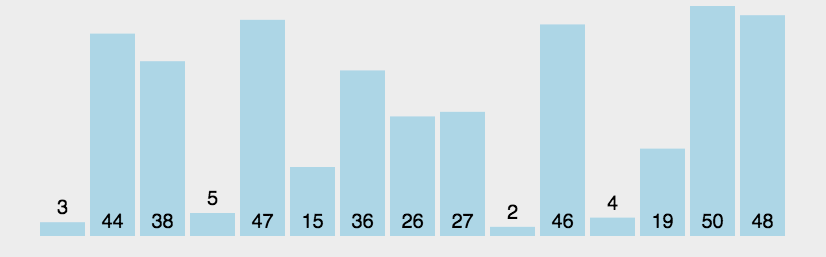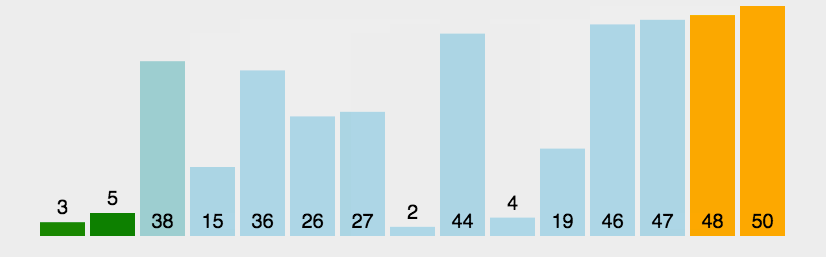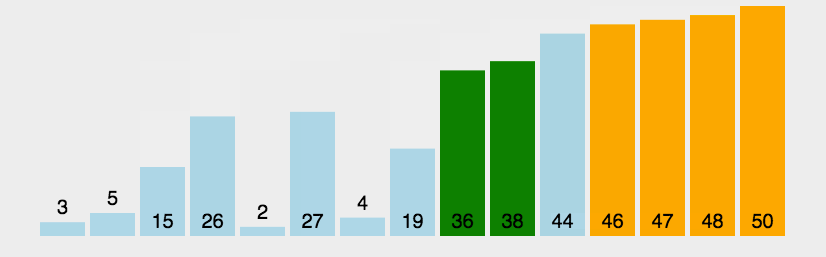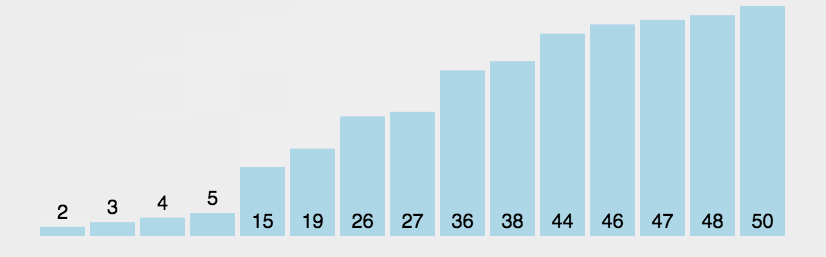
交换排序，它的核心思想就是通过不断的交换，使得每个数据都呆在应该在的位置（有序），应该呆在的位置就是左边的比它小，右边的比它大的位置。冒泡排序和快速排序都是利用了交换排序的思想，通过交换使得数据组有序，不过俩者交换的办法不同。

2.3.1 冒泡排序

我相信大家第一个学习的排序算法就是冒泡排序，它相对简单。但是大家学习的冒泡排序不一定正宗
冒泡排序的基本思想就是：两两比较相邻的数，如果是反序就交换，直到没有反序就停止交换。

（1） 简易交换排序
这个排序就是大家平常写的冒泡排序，我之所以说它不正宗，是因为它不满足两两相连比较，它只是简单的交换排序。

void Bulle_sort1(int* arry, int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = i + 1; j < n; j++)
		{
			if (arry[i] > arry[j])
				Swap(&arry[i], &arry[j]);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11

分析一下这个排序的代码：用 i 来控制边界，j 是 i 的下一个数的下标，只要 i 下标之后的数大于arry[i],我们就交换一下，走第一趟会使i=0的位置的数为最小的数，i++后i=1，j=2，继续在后面的数里找比arry[1]还有小的数，找到了就交换一下。就是这样最终数组在这种交换下有序。
还是惯例画图看一下，比如排下面这个数组：

因为5>4,所以交换一下。

因为4<9，所以不交换，3<4交换一下。

因为1<3,交换。

以上就是一趟排序走下来，下标为0处的位置是最小值1，所以继续往下排序，不出所料，下标为1处被换上了次小值3，讲到这我相信大家是明白了。
(2)冒泡排序
接下来就将正宗的冒泡排序。
代码如下：

void Bulle_sort2(int* arry, int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = n-1; j >= i; j--)
		{
			if (arry[j] <arry[j-1])
				Swap(&arry[j], &arry[j-1]);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11

它正宗之处就在于，它是通过两两相邻比较的方式来交换，而且它会把最小的数像气泡一样让它冒上去，这说的有点抽象我们画图看一下。

排下面这个数组，这里就竖着吧

根据代码是从末尾往上两两相邻比较交换的，所以1<14交换一下。

不赘述了，反正从后往上两两比较以及交换。所以1被换到了顶上。

就是这样像冒泡一样，再从后往上两两比较交换，使得数组最终有序。
（3）:冒泡排序优化

冒泡排序的优化，主要在于优化那些没必要的比较。比如我已经有序了，就不需要比较交换，但是冒泡排序不晓得你有没有序，于是还傻乎乎的在比较呢。为此我们可以搞一个flag来标志有没有序。

void Bulle_sort3(int* arry, int n)
{
	int flag = 0;
	for (int i = 0; i < n; i++)
	{
		flag = 1;
		for (int j = n-1; j >= i; j--)
		{
			if (arry[j] < arry[j - 1])
			{
				Swap(&arry[j], &arry[j - 1]);
				flag = 0;
			}
		}
		if (flag == 1)
			break;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

flag如果是1，那就说明这趟排序我没有交换数据，没有交换数据就说明已经有序了。对吧，大家好好悟一下。

2.3.2 快速排序

快速排序，简称快排，那特点就是快。虽然和冒泡排序一样都是交换排序的思想，但是它俩的排序速度差的不是一星半点。我们不难发现冒泡排序每次跑一趟结果就是将下面的数中最小的冒到上面，也就是使最小的数来到了它合适的位置。快排不一样，它是用更短的时间，让某个数来到它合适的位置，这位置不一定在顶上，就是适合它的位置，左边的数比它小右边的数比它大。当然也是通过比较和交换的方式。

（1）：画图理解一下快排
left左边界，right右边界，pos指向我想让它去合适位置的数

right往左走找到了比pos位置处小的数就停下，left往右走找到比pos位置处大的数就停下。

将left和right的数交换，left

右边继续找小数，左边找的数，找到了就交换一下。


left
走到这个位置，因为left>right,所以不交换，直接退出循环，在将pos处的值和right处的值交换。

可以看到11的左边的数都比它小，右边的数都比它要大，所以就找到它合适的位置。为了让数组整体有序我们应该怎么办？有的同学会想到让pos++，然后改变一下left和right的边界重复上面的过程就可以了，等pos指向最后一个数，这个数组就有序了。这确实是一种办法，但是不好。不够快。所以这里需要利用递归来解决。有点像二叉树，我们根据这个11，可以划分出两个区间，左区间和右区间，让左区间和右区间都有序，这个数组就有序了。这样比第一种想法要快。
（2）:代码讲解

int Partition(int* arry, int left, int right)//交换用的函数，调用一次就找到一次合适位置
{
	int pos = left;//默认选择左边数，这其实有问题后面讲
	while (left < right)
	{
		while (left < right && arry[right] >= arry[pos])//右边的找小的数，找到就停下
			right--;
		while (left < right && arry[left] <= arry[pos])//左边的找大的数，找到就停下
			left++;
		Swap(&arry[left], &arry[right]);//交换一下两值
	}
	Swap(&arry[pos], &arry[right]);//将其放在合适位置
	return right;//返回其位置
}
void Quick_sort(int* arry, int left, int right)
{
	int pos;
	if (left < right)
	{
		pos = Partition(arry, left, right);
		Quick_sort(arry, left, pos - 1);//递归左区间
		Quick_sort(arry, pos + 1, right);//递归右区间
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

我们来分析一下代码：
Partition函数就是我们用于将选中的数放在合适的位置，默认选中最左边边的数。相当于走一趟，将一个数放到其合适位置。最后返回了这个合适位置（下标），据此数组就被分成了两部分，使左部分和右部分都有序，就完成了排序。也就是这段代码：

pos = Partition(arry, left, right);
		Quick_sort(arry, left, pos - 1);//递归左区间
		Quick_sort(arry, pos + 1, right);//递归右区间
1
2
3

但是这样完成的快排还有缺陷，就是默认选择去排最左边的数，这会导致出现一些问题，如果这个数排完后不在中间而是两边，就会导致无法分出俩个区间而是只得到一个区间，如图：

被分成这样的两个区间，这样其实没有优化，我们动脑子想想如果这个数组有序，我们往下排序的时候一直都会遇见这种情况，相当于变了样的冒泡排序。所以针对这种情况有了三数取中这个方法，甚至还有九数取中。就是为了取数时，取一个中间一点的值，防止选到直接蹦到两边的值。

//三数取中
int GetMidIndex(int* a, int left, int right)
{
	//int mid = (left + right) / 2;
	int mid = left + ((right - left) >> 1);
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
int Partition(int* arry, int left, int right)
{
    //得到三数取中的返回值
	int mi = GetMidIndex(arry, left, right);
	//将两值交换，使得最左边值为三数中间值
	Swap(&arry[mi], &arry[left]);
    //以下逻辑一样，保持不变
	int pos = left;
	while (left < right)
	{
		while (left < right && arry[right] >= arry[pos])
			right--;
		while (left < right && arry[left] <= arry[pos])
			left++;
		Swap(&arry[left], &arry[right]);
	}
	Swap(&arry[pos], &arry[right]);
	return right;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

加上三数取中后，快排就完成了，遇到有序的数组也可以解决问题。但是，现在的快排还不是无敌的，因为我们是用递归来完成的快排，大家知道栈的空间有限不算大，如果递归的深度很大就会导致栈溢出，无法完成排序。所以我们不用递归来完成快排，这样在面对超级大量的数据时，也不用担心栈溢出。

void QuickSortNonR(int* a, int left, int right)
{
	ST st;//这是我自定义的栈
	StackInit(&st);//栈的初始化
	StackPush(&st, left);//将左下标入栈
	StackPush(&st, right);//右下标也入栈

	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);//取出栈顶元素，再pop掉
		StackPop(&st);

		int begin = StackTop(&st);//再取出栈顶元素，pop掉
		StackPop(&st);

		int keyi =  Partition(a, begin, end);//排一趟序，使得keyi在合适位置
		// [begin, keyi-1] keyi [keyi+1, end]//分成了这样的两端区间
		if (keyi + 1 < end)//满足条件说明，依旧有区间需要排
		{
			StackPush(&st, keyi+1);//将左右下标入栈
			StackPush(&st, end);
		}

		if (begin < keyi-1)//同上
		{
			StackPush(&st, begin);
			StackPush(&st, keyi-1);
		}
	}

	StackDestroy(&st);//销毁栈
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

完成上面的快排，利用了栈这种数据结构，如果不了解栈数据结构的可以直接略过这个版本的快排。用栈来存储区间的左右下标。然后通过记录下标，来完成各个区间的排序，像递归的话比较直接就是用函数调用来完成各个区间的排序。当栈里没有数据时，说明排序已经完成。

---

2.4 归并排序

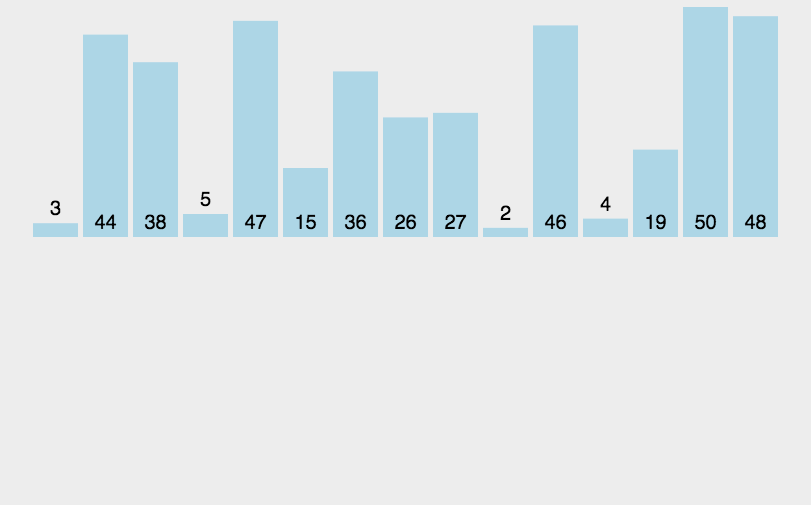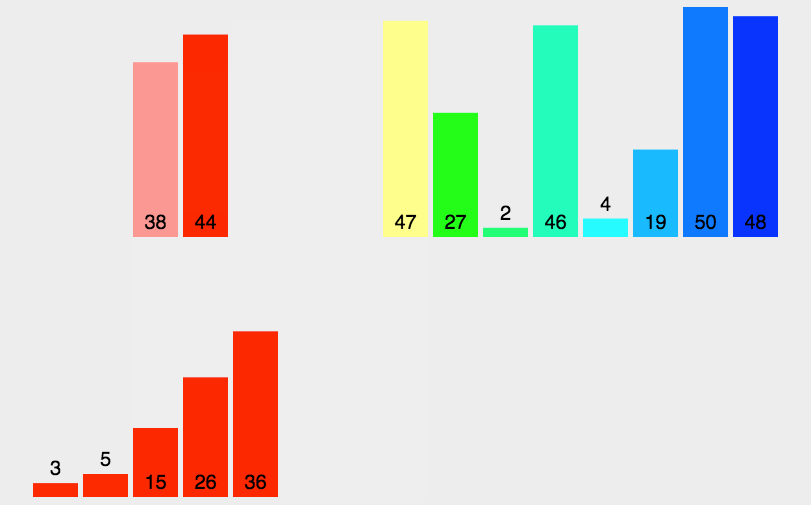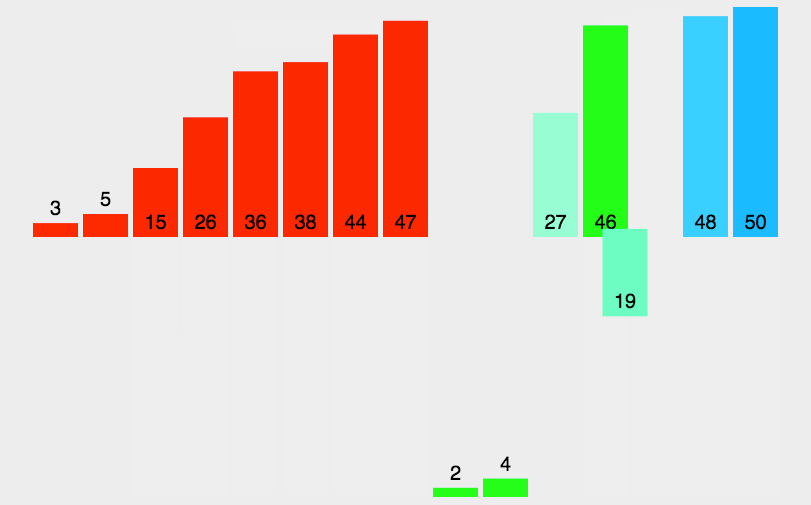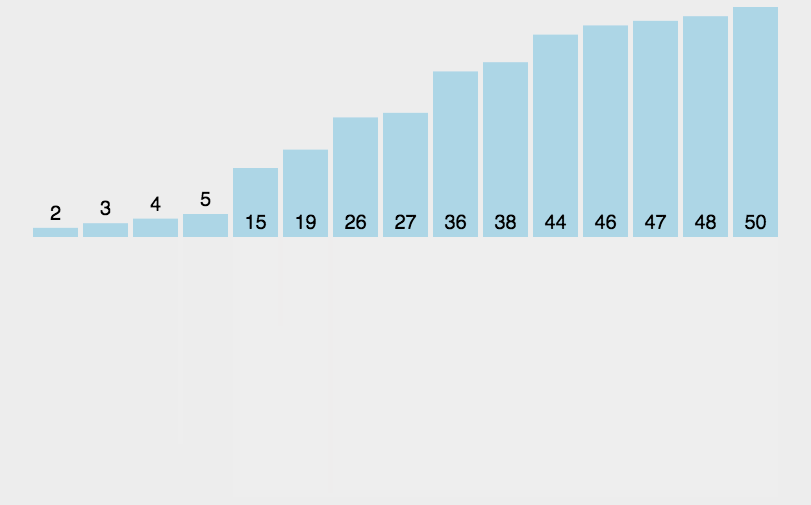
归并排序，有合并，并入的思想。如果一个数组，分成两个区间，这两个区间分别有序，再对这两个区间进行合并，那么数组就有序了。那么问题就来了，分成的俩个区间如果有序呢？可以再让这俩小区间继续分裂，直到分成俩个只有一个数的区间，这样再开始合并，不断的往上合并最终就有序了。

(1)画图理解归并排序
(1)如下数组，分成两个区间。

(2)不断的分区间，直到分成一个一个的数，然后开始归并，归并的过程就是在排序。

(3)开始归并

(4)就这样继续归并，直到全体归并一起。

（2）代码讲解归并排序

void _Mergesort(int* arry, int left, int right,int *tmp)
{
	if (left >= right)//当分到1个为1组的时候就返回了
		return;
	int mid = (left + right) / 2;//取中间下标以分区间
	//[left,mid][mid+1,right]
		_Mergesort(arry, left, mid,tmp);//左区间向下分
		_Mergesort(arry, mid + 1, right,tmp);//右区间向下分
		//走到这里说明上面已经分好了开始归并
		int begin1 = left; int end1 = mid;//左区间
		int begin2 = mid + 1; int end2 = right;//右区间
		int i = left;//i来控制tmp数组的下标
		//这个循环就是在往tmp数组里并数据，我下面会讲
		while (begin1 <= end1 && begin2 <= end2)
		{
			if (arry[begin1] < arry[begin2])
				tmp[i++] = arry[begin1++];
			else
				tmp[i++] = arry[begin2++];
	    }
	    //剩下的也往tmp里面归并
		while (begin1 <=end1)
		{
			tmp[i++] = arry[begin1++];
		}
		while (begin2 <= end2)
		{
			tmp[i++] = arry[begin2++];
		}
		//将tmp的值拷贝到arry里面
		for (int j = left; j <= right; j++)
		{
			arry[j] = tmp[j];
		}
}
void Merge_sort(int* arry, int n)
{
    //tmp数组用于放排序好的数组
	int* tmp = (int*)malloc(sizeof(int) * n);
	//调用归并函数
	_Mergesort(arry, 0, n-1,tmp);
	free(tmp);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

上面的代码一遍不好看懂，我们来画一画递归展开图，帮助大家理解。

(1)首先，Merge_sort函数里创建了一个tmp数组用于放归并好的数据。然后调用了，_Mergesort(arry, 0, n-1,tmp)函数。n=6。
第一次进入_Mergesort函数，mid=2，继续递归。

(2)第二次进入_Mergesort函数，这是在递归左区间[0,2],mid=1;

(3)第三次进入_Mergesort函数，这是在递归区间 [0,2] 的左区间[0,1],mid=0;

(4)第四次进入_Mergesort函数，这是在递归区间 [0,1] 的左区间[0,0]，这就递归到单个数的时候了，要返回了。right == left。

(5)返回到上一级，也就是第三次调用的时候，

(6)所以应该递归[0,1]的右区间[1,1],

(7)因为left == right，所以返回。开始归并了哦！俩个孤独的灵魂要走在一起了。其实走到这步，我们就完成了[0,1]区间的归并操作，然后返回到它的上一级也就是[0,2],开始递归它的右区间[2,2]。


(8)2==2，所以返回上一级[0,2]。返回之后，就是[0,1]和[2,2]的归并。它俩都有序，[2,2]一个数肯定有序。[0,2]归并成功后返回上一级也就是[0,5]。返回[0,5]后，它的左区间[0,2]已经有序开始递归它右区间[3,5],过程和递归[0,2]类似。

(9)就是这样[3,5]的过程我就不赘述了，直接跳到[3,5]归并成功后，然后[0,2]和[3,5]一归并，整个区间[0,5]就有序了。

(10)就是这样，归并排序的全过程。
接下来讲一讲是如何归并的，其实这个问题可以阐述为：将两个有序的数组合并在一起。我还刷到过这个题在牛客上。
将下面的俩个数组归并下面的tmp数组里面，i来控制tmp的下标。
(1)比较left1和left2所指向的值，谁小谁就放到tmp里并且i++,放进去值的left也加1。

(2)因为1<2，所以1放下去，i++，left1++；再继续比较。
(3)俩两，比较直到到某一个left走完，可以看到现在left2走完了，left1里还有剩余的数，再将left1剩余数拷贝进tmp即可。

(4)完成了。

这就是图解。希望对大家有帮助吧。

2.5计数排序

学到这里我们可以发现，以上排序最多只能做到O(n*logⁿ),有没有更优的排序，可以做到O(n),O(n)基本上可以说是排序的天花板了，也就是遍历几遍就能做到有序。接下来，我就介绍这种排序：计数排序，它的时间复杂度可以做到O(n)，它的思想就是用一个数组count来存放要排序数组arry中数字出现的个数，具体存在count的哪个位置，这个有映射关系。

我们来画图理解一下计数排序。
(1)下图就是我们要排序的数组arry，和存放数字出现个数的数组count。

（2）遍历arry数组，可以发现 7出现2次，2出现2次，1出现2次，3出现一次，0出现一次，没出现的填0。所以填到count数组里，这里建立的映射关系是arry数字和count下标相等。

（3）然后根据count数组统计的，对arry进行排序。

就是用这种方式来进行排序，它没有通过比较来进行排序，而是开辟了一个数组用记录以及映射关系来完成排序。

但是还有一个问题，这种下标和数相等的映射关系，存在很大的空间浪费，比如下面这种情况。

因为里面出现一个数字1000，所以开辟count数组时，必须开辟1000以上大小的数组，这就导致很严重的空间浪费，所以这种数据不集中的数组，不建议用计数排序。同时为了减少空间浪费。我们可以开辟出最大值-最小值+1的空间，数字的大小=count下标+最小值。

代码实现：

void CountSort(int* a, int n)
{
	//算出最大值和最小值相减得到count数组空间都大小
	int max = a[0], min = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}

		if (a[i] < min)
		{
			min = a[i];
		}
	}
	//range为count数组的大小
	int range = max - min + 1;
	//count开辟空间
	int* count = (int*)malloc(sizeof(int) * range);
	//初始化count，默认为0
	memset(count, 0, sizeof(int) * range);
	// 统计次数
	for (int i = 0; i < n; ++i)
	{
		//对应位置的数出现就加1
		count[a[i] - min]++;
	}

	// 根据次数，进行排序
	int j = 0;
	for (int i = 0; i < range; ++i)
	{
		//count[i]存的是出现的次数
		while (count[i]--)
		{
			//这个数的大小是i+min
			a[j++] = i + min;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

---

3，排序算法总结

终于到了，排序算法总结这里，我们来对以上的所有排序进行个比较。

各个排序都有它优秀的地方，虽然冒泡，直接插入排序大部分情况是O(n²),但是面对基本有序的数组时，它的性能是O(n)。这里有个巧妙比喻，大学教授去教小学生，不一定有小学老师教的好。所以在面对基本有序这种小学生，冒泡和直接插入足以。通过比较发现归并和堆排是比较优秀的排序，它在面对任何情况都能稳定发挥。快速排序也很强但是在最坏情况下会发挥失常直接成O(n²)。从稳定性上看，归并太棒了，又快又稳定。排序各有春秋，它能不能发挥出它的力量关键是能不能遇见一个伯乐去使用。

---

结束语: 排序，本篇博客介绍了八个，其实还有排序没讲到，不是还有十大排序嘛，少讲了两个上面图里还打马赛克了，博主主要是认为那两个排序在工作中基本用不到，所以就省略了。掌握以上八个排序就够了。希望大家学有所成。