OFDM 十六讲 4 -What is a Cyclic Prefix in OFDM

参考   

     

    OFM 里面重点是ISI,ICI, CP.这里面重点讲解一下CP. Cyclic prefix，循环前缀

也有很多博客文档讲过这个,外文有专门的一本书讲CP，这篇主要是初步了解CP，

如果有兴趣可以把CP 跟 各种 调制模式,以及星座图结合起来分析,多普勒效应结合起来研究。

之前在Bilibili 也看过爱立信的专家有用机器学习去做这块模型研究的。

目录：

1: single - carrier situation

2: multi - carrier situation

3  DFT & IDFT code

4:  常用三角函数公式

---

一  single -carrier 

    1.1 BPSK 译码问题

     

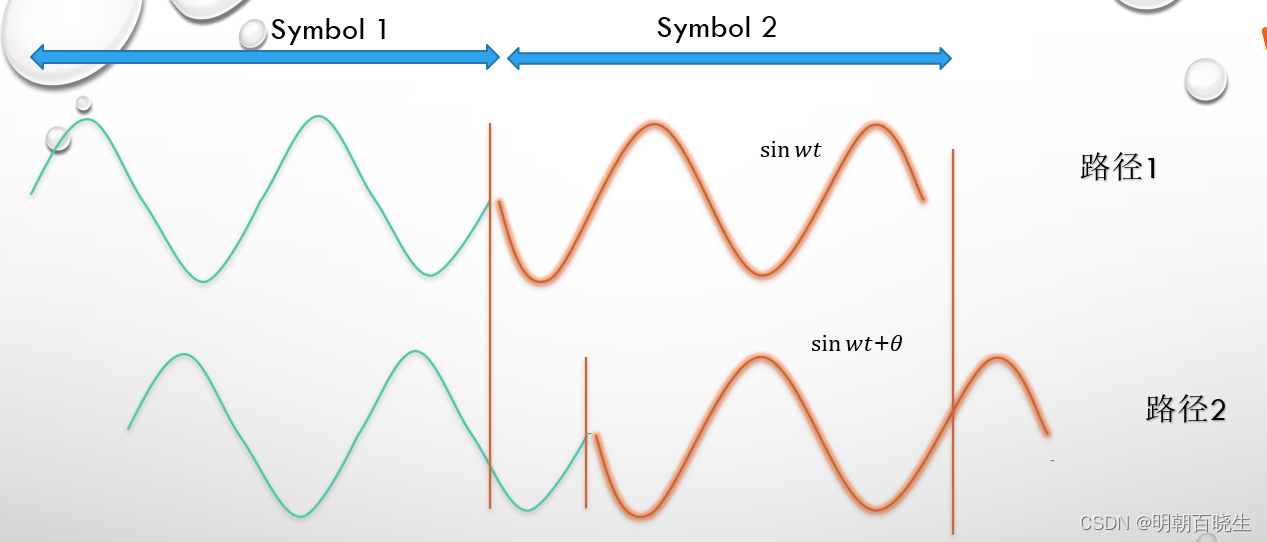
      这里面我们以BPSK modulation 为例，发送两个symbols,

接收方想要译码出symbols 2 的时候，由于多径传输问题

  假设原始发射的信号为：

   

   收到的信号为

    

   根据和差化积公式

    

  我们放到星座图里面看

 1.2  星座图

 

  通过星座图可以看到：相位和幅度都发生了变化。

  如果相位超过90度，会导致译码出错。

1.3   解决方案

 每个发送符号的前面加一个循环前缀,发送的信息格式  cp+msg

 解码只解码msg 部分,cp部分discard.

缺点：

     循环前缀长度越长,信道效率越低。

 cp: 是发送symbols 1周期或几个周期的的组成

1.4  symbol 1 译码

  如上图,symbols 1：

  发送信息 ： cp+msg

  译码的时候：

           在采样窗口，第二个周期泄露掉的功率通过cp 泄露出来的功率补上了。

1.5 symbol2

   

    原始信息是2个周期的正弦波，加上一个一个周期的cp

    解码的时候，cp 部分丢弃

    在采样窗口内，最后一个周期泄露出的能量，通过cp  部分能量补上了。

---

二   multi-carrier situation for ofdm

     

    OFDM 通过离散傅里叶逆变换把输入的频域信息转换为时域信息

     

   因为信号是叠加后的信号，没有单载波的周期了。解决方案，是把信号的后面一部分

拿到前面做为CP。

   译码的时候跟single-carrier 是一样的，如下 后面leak out 的energy， 通过前面的

cp 部分补上来。

 译码的时候，首先要重组,先把采样周期内CP 的长度拿到后面去

---

三  DFT & IDFT

   DFT  公式

   

   IDFT 公式

   

# -*- coding: utf-8 -*-
"""
Created on Tue Aug  2 11:51:23 2022
@author: chengxf2
"""
import numpy as np
 
#离散傅里叶变换#
def DFT(X):
    N = len(X)
    
    real  =[] #傅里叶变换的实部 cos
    img=[]  #傅里叶变换虚部 sin
    
    for k in range(N):
        
        w = -(2*np.math.pi/N)*k #角频率
        
        i = 0 
        q = 0
        for t in range(N):
            x = X[t]
            theta = w*t #相位
            
            i = i+x*np.cos(theta)
            q = q+x*np.sin(theta)
        i = np.round(i,2)
        q = np.round(q,2)
        real.append(i)
        img.append(q)
    print(real)
    print(img)
    return real,img
 
#离散傅里叶逆变换#
def IDFT(real, img):
    
    N = len(real)
    
    for t in range(N):
    
        im = 0    
        
        for k in range(N):
            w = (2*np.math.pi/N)*k #角频率
            theta = w*t
            a = np.cos(theta)*real[k]
            b = np.sin(theta)*img[k]
            im += (a-b)
            #b = b+q
        im= im/N
        im = np.round(im,1)
        
        #b = b/N
        #print("\n  时域信息 X[%d] = %d "%(t,im))
    
X =[1,2,3,4,5,6,7,8,9]
real,img =DFT(X)
 
 
IDFT(real,img)

---