目录

LCA

树的统计

LCA

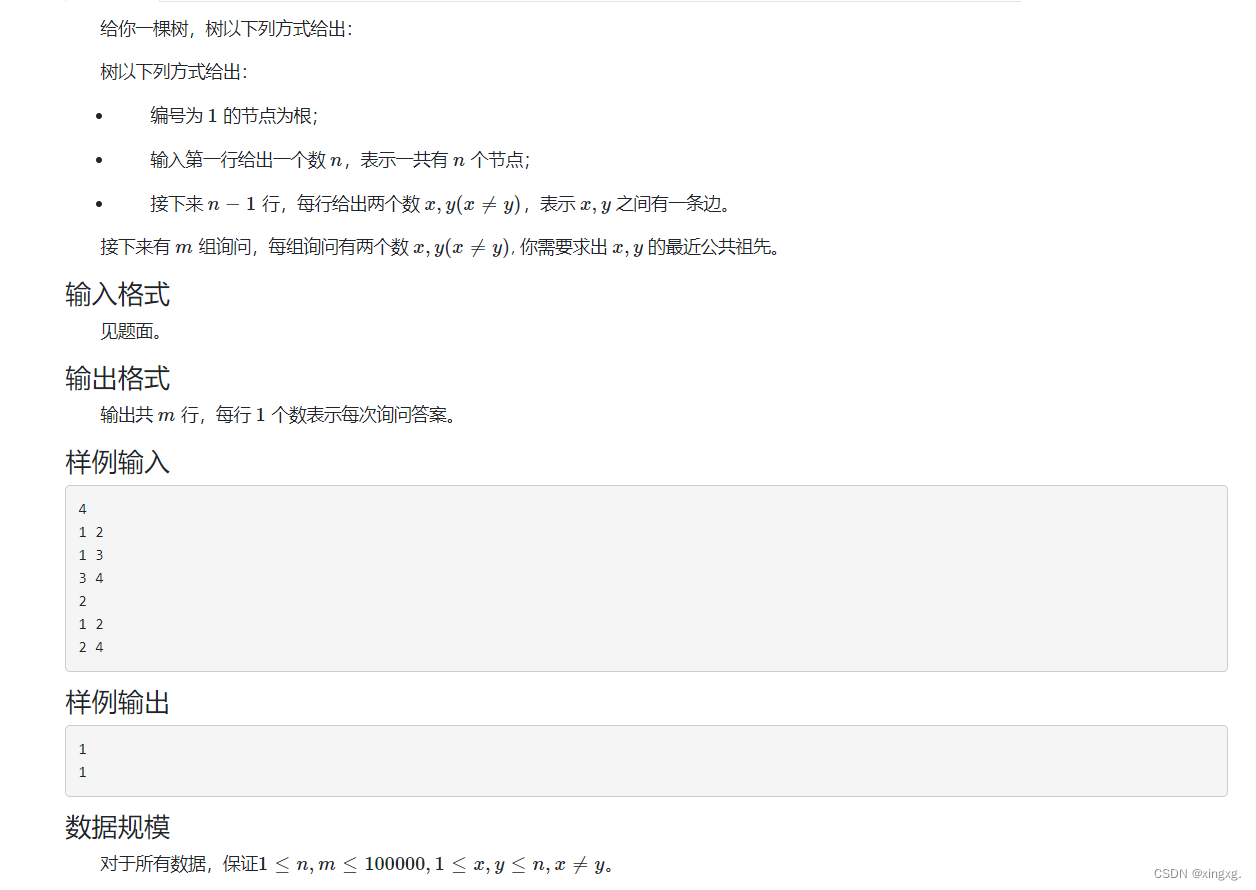
 LCA问题，可以使用之前的倍增来解决，这里也可以用树链剖分来处理。

树链剖分一般也叫做重链剖分（无特殊说明）。另一种是长链剖分。重链剖分跟重儿子的定义一样，也是节点数最多的。

每一个节点都会有一条重边（也就是在孩子中找出一个节点数最多的子树。）这些重边就会形成一条重链。

树链剖分的特点：

        

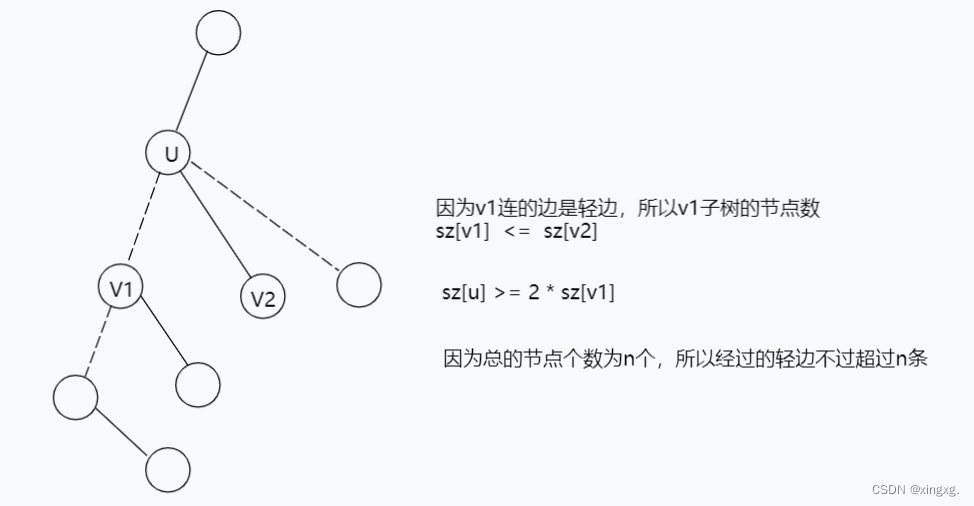
        每个点都会连接一条重链的，可能这条重链的长度只有1，可能这个点就是这条重链的顶端。           一段重链 —— 一条轻链 —— 一段重链 —— 一条轻链 —— 一段重链 ... 

// problem :  
 
#include 
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define pb push_back
const int N = 101000;
int sz[N], hs[N], fa[N], dep[N], id[N], l[N], r[N], top[N];
std::vector<int> e[N];
int tot, n, m;
void dfs1(int u, int f) {
    sz[u] = 1;
    hs[u] = -1;
    fa[u] = f;
    dep[u] = dep[f] + 1;
    for (auto v : e[u]) {
        if (v == f) continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (hs[u] == -1 || sz[hs[u]] < sz[v])
            hs[u] = v;
    }
}
 
void dfs2(int u, int t) {
    top[u] = t;
    // l[u] = ++tot;
    // id[tot] = u;
    if (hs[u] != -1) {
        dfs2(hs[u], t);
    }
    for (auto v : e[u]) {
        if (v != fa[u] && v != hs[u])
            dfs2(v, v);
    }
    // r[u] = tot;
}
 
int LCA(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) v = fa[top[v]];
        else u = fa[top[u]];
    }
    if (dep[u] < dep[v]) return u;
    else return v;
} 
int main(){
    scanf("%d", &n);
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d %d", &u, &v);
        e[u].push_back(v);
        e[v].push_back(u);
    }   
    dfs1(1, 0);
    dfs2(1, 1);
    scanf("%d", &m);
    for (int i = 1; i <= m; ++i) {
        int u, v;
        scanf("%d %d", &u, &v);
        printf("%d\n", LCA(u, v));
    }
    return 0;
}

树的统计

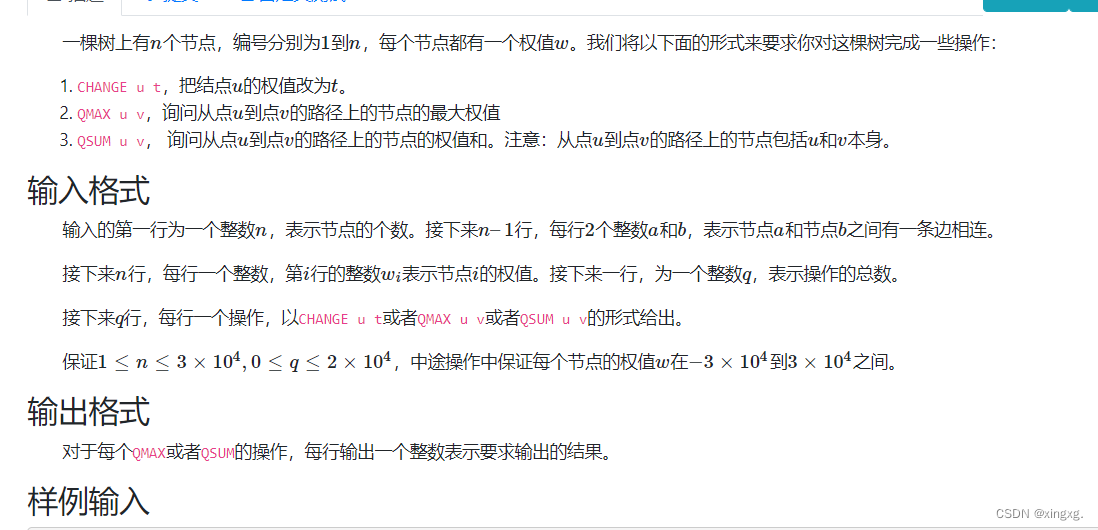
 将树链剖分、线段树结合在一起。模板题。   树链剖分 + DFS序（优先遍历重边，使得重边的序号是连续的），在DFS序的基础上，建线段树。

要清楚DFS序中  l、r数组代表的含义，以及idx数组代表的意思。     

idx[i] ,  第i个DFS序的所对应的节点编号，建线段树时赋初值用到。 

l[u]  : u 节点对应的DFS序的左区间，同时也是第l[u]遍历到的点

// problem :  
 
#include 
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define pb push_back
const int N = 101000;
int n, m, a[N]; // 读入
std::vector<int> e[N]; // 读入
int sz[N], hs[N], fa[N], dep[N], top[N]; // 树链剖分
int l[N], r[N], tot, idx[N]; // DFS序
void dfs1(int u, int f) {
    sz[u] = 1;
    hs[u] = -1;
    fa[u] = f;
    dep[u] = dep[f] + 1;
    for (auto v : e[u]) {
        if (v == f) continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if (hs[u] == -1 || sz[hs[u]] < sz[v])
            hs[u] = v;
    }
}
 
void dfs2(int u, int t) {
    top[u] = t;
    l[u] = ++tot;
    idx[tot] = u;
    if (hs[u] != -1) {
        dfs2(hs[u], t);
    }
    for (auto v : e[u]) {
        if (v != fa[u] && v != hs[u])
            dfs2(v, v);
    }
    r[u] = tot;
}
 
struct info {
    int maxv, sum;
};
info operator + (const info &l, const info &r) {
    info ans;
    ans.maxv = max(l.maxv, r.maxv);
    ans.sum = l.sum + r.sum;
    return ans;
}
struct node {
    info val;
}seg[N * 4];
 
void update(int id) {
    seg[id].val = seg[id * 2].val + seg[id * 2 + 1].val;
}
void build(int id, int l, int r){  // 基于DFS序建线段树，不是节点1-n
    if(l == r) {
        // L号点，DFS序中的第L个点
        seg[id].val = {a[idx[l]], a[idx[l]]};
    } else {
        int mid = (l + r) / 2;
        build(id * 2, l, mid);
        build(id * 2 + 1, mid + 1, r);
        update(id);
    }
}
 
void change(int id, int l, int r, int pos, int val) {
    if(l == r) {
        seg[id].val = {val, val};
    } else {
        int mid = (l + r) / 2;
        if(pos <= mid) change(id * 2, l, mid, pos, val);
        else change(id * 2 + 1, mid + 1, r, pos, val);
        update(id);
    }
}
 
info query(int id, int l, int r, int ql, int qr) {
    if(ql == l && qr == r) {
        return seg[id].val;
    }
    int mid = (l + r) / 2;
    if(qr <= mid) return query(id * 2, l, mid, ql, qr);
    else if(ql > mid) return query(id * 2 + 1, mid + 1, r, ql, qr);
    else return query(id * 2, l, mid, ql, mid) +
        query(id * 2 + 1, mid + 1, r, mid + 1, qr);
}
 
info query(int u, int v) {
    info ans {(int) -1e9, 0};
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) {
            ans = ans + query(1, 1, n, l[top[v]], l[v]);
            v = fa[top[v]];
        } else {
            ans = ans + query(1, 1, n, l[top[u]], l[u]);
            u = fa[top[u]];
        }
    }
    if (dep[u] <= dep[v]) ans = ans + query(1, 1, n, l[u], l[v]);
    else ans = ans + query(1, 1, n, l[v], l[u]);
    return ans;
}
 
int main(){
    scanf("%d", &n);
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d %d", &u, &v);
        e[u].push_back(v);
        e[v].push_back(u);
    }   
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    dfs1(1, 0);
    dfs2(1, 1);
    build(1, 1, n);
    scanf("%d", &m);
    for (int i = 1; i <= m; ++i) {
        int u, v;
        static char op[10];
        scanf("%s%d %d", op, &u, &v);
        if (op[0] == 'C') {
            change(1, 1, n, l[u], v);
        } else {
            info ans = query(u, v);
            if (op[1] == 'M') printf("%d\n", ans.maxv);
            else printf("%d\n", ans.sum);
        }
    }
    return 0;
}