1. 树型结构（了解）

1.1 概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

1. 有一个特殊的结点，称为根结点，根结点没有前驱结点
2. 除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm，其中每一个集合 Ti (1 <= i
   <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
3. 树是递归定义的。

注意：树形结构中，子树之间不能有交集，否则就不是树形结构

1.2 概念（重要）

1. 结点的度：一个结点含有子树的个数称为该结点的度； 如上图：A的度为6
2. 树的度：一棵树中，所有结点度的最大值称为树的度； 如上图：树的度为6
3. 叶子结点或终端结点：度为0的结点称为叶结点； 如上图：B、C、H、I…等节点为叶结点
4. 双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点
5. 孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点
6. 根结点：一棵树中，没有双亲结点的结点；如上图：A
7. 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
8. 树的高度或深度：树中结点的最大层次； 如上图：树的高度为4
   树的以下概念只需了解，在看书时只要知道是什么意思即可
9. 兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：B、C是兄弟结点
10. 堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点
11. 结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先
12. 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙
13. 森林：由m（m>=0）棵互不相交的树组成的集合称为森林
14. 非终端结点或分支结点：度不为0的结点； 如上图：D、E、F、G…等节点为分支结点

1.3 树的表示形式（了解）

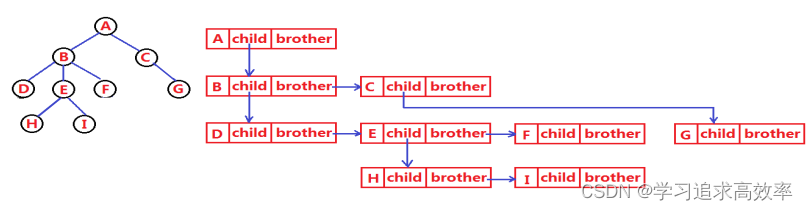
树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

class Node { 
	int value; // 树中存储的数据 
	Node firstChild; // 第一个孩子引用 
	Node nextBrother; // 下一个兄弟引用 
}
1
2
3
4
5

1.4 树的应用

文件系统管理（目录和文件）

2. 二叉树（重点）

2.1 概念

一棵二叉树是结点的一个有限集合，该集合：

1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成
   从上图可以看出：

1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

注意：对于任意的二叉树都是由以下几种情况复合而成的：

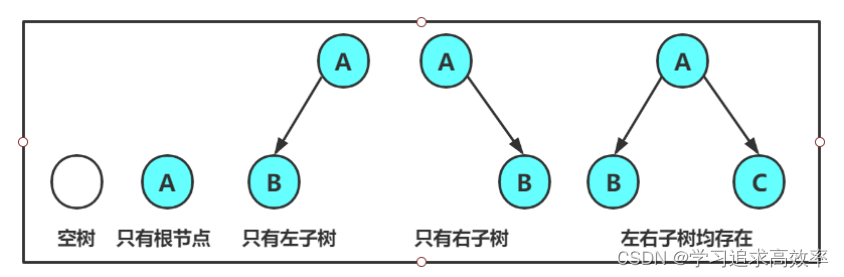
2.2 两种特殊的二叉树

2.3 二叉树的性质

3. 第三个性质 n0 = n2 + n1

利用的是 1.N个节点 = 度数节点相加 2. N - 1 条边 = 度数相加

例题

例题 2 偶数节点（存在一个度为1的节点）

例题 3 奇偶节点数

2.4 二叉树的存储

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，具体如下：

// 孩子表示法
class Node { 
	int val; // 数据域 
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 }

// 孩子双亲表示法
class Node { 
	int val; // 数据域 
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 
	Node parent; // 当前节点的根节点 
}
1
2
3
4
5
6
7
8
9
10
11
12
13

孩子双亲表示法后序在平衡树位置介绍，本文采用孩子表示法来构建二叉树

2.5 二叉树的基本操作

2.5.1 前置说明（二叉树的存储）

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式

class BinaryTree{

    public static class BTNode{
        BTNode left;
        BTNode right;
        int value;
        BTNode(int value){
            this.value = value;
        }
    }
    
    private BTNode root;
    
    public void createBinaryTree(){
        BTNode node1 = new BTNode(1);
        BTNode node2 = new BTNode(2);
        BTNode node3 = new BTNode(3);
        BTNode node4 = new BTNode(4);
        BTNode node5 = new BTNode(5);
        BTNode node6 = new BTNode(6);
        root = node1;
        node1.left = node2;
        node2.left = node3;
        node1.right = node4;
        node4.left = node5;
        node5.right = node6;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的
   从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的

2.5.2 二叉树的遍历

1. 前中后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结
点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如：打印节点内容、节点内容加
1)。 遍历是二叉树上最重要的操作之一，是二叉树上进行其它运算之基础
在遍历二叉树时，如果没有进行某种约定，每个人都按照自己的方式遍历，得出的结果就比较混乱，如果按
照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点，L代表根节点的
左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式

1. NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
2. LNR：中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
3. LRN：后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点

1.前序遍历（每次遍历的节点都先当做根）

2. 中序遍历（只有把根的左子树遍历完，再打印根）

3. 后序遍历（只有把左右子树都遍历完，再打印根）

前序递归遍历
前序遍历结果：1 2 3 4 5 6（每次遍历的节点都先当做根）
中序遍历结果：3 2 1 5 4 6（只有把根的左子树遍历完，再打印根）
后序遍历结果：3 1 5 6 4 1（只有把左右子树都遍历完，再打印根）

2. 层序遍历

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层
上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历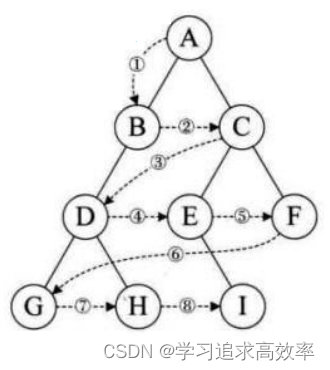

例题（关键：找根）

【练习】请根据以上二叉树的三种遍历方式，给出以下二叉树的：
选择题

补充：完全二叉树的 层序遍历（画图容易）

2.5.3 二叉树的基本操作

1. 求树中的节点个数 size

方法1：直接return（子问题思路）

方法2：利用返回值 相加return（子问题思路）

方法3：静态值（遍历思路）

	// 子问题思路  获取树中节点的个数
	int size(TreeNode root) {
	    if(root == null) return 0;
	    return size(root.left) + size(root.right) + 1;
	}
	//遍历思路：只要遍历到了节点 就nodeSize ++
	public static int nodeSize;
	void size2(TreeNode root) {
	    if(root == null) return;
	    nodeSize++;
	    size2(root.left);
	    size2(root.right);
	}
    /*
     * 利用返回值递归求节点个数
     * */
    int size3(TreeNode root){
        if(root == null)return 0;
        int ret = 1;
        ret += size3(root.left);
        ret += size3(root.right);
        return ret;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

2. 求二叉树中 叶子结点个数 getLeafNodeCount

如何判断叶子节点

if(root.left == null && root.right == null)
1

    //子问题 获取叶子节点的个数
    int getLeafNodeCount(TreeNode root) {
        if(root == null) {
            return 0;
        }
        if(root.left == null && root.right == null) {
            return 1;
        }
        return getLeafNodeCount(root.left)
                + getLeafNodeCount(root.right);
    }

    //遍历思路
    public static int leafSize;
    void getLeafNodeCount2(TreeNode root) {
        if(root == null) return;
        if(root.left == null && root.right == null) {
            leafSize++;
        }
        getLeafNodeCount2(root.left);
        getLeafNodeCount2(root.right);
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3. 获取第K层节点的个数 getKLevelNodeCount

递归中 k-- 和 k-1 不一样

    // 获取第K层节点的个数
    int getKLevelNodeCount(TreeNode root,int k) {
        if(root == null) return 0;
        if(k == 1) {
            return 1;
        }
        return getKLevelNodeCount(root.left, k-1) +
                getKLevelNodeCount(root.right,k-1);
    }
1
2
3
4
5
6
7
8
9

4. 获取二叉树的高度 时间复杂度：O(N) getHeight

    // 获取二叉树的高度  时间复杂度：O(N)
    int getHeight(TreeNode root) {
        if(root == null) return 0;
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return (leftHeight > rightHeight ?
                leftHeight+1 : rightHeight+1);
    }
1
2
3
4
5
6
7
8

*****5. 检测值为value的元素是否存在

*****子问题递归思想：原则就是只根据一个根节点分析就好

原则就是只根据一个根节点分析就好
分析如下：
分析A节点
如果A节点的值是 key
那么返回A节点
否则遍历左节点
如果左节点返回的值不是 空 那么就返回返回值
如果左节点返回值是空 那么就 遍历右节点
如果右节点的返回值不是空 那么就返回返回值
否则就直接返回空

// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val) {
    if(root == null) return null;
    if(root.val == val) {
        return root;
    }
    TreeNode ret1 = find(root.left,val);
    if(ret1 != null) {
        return ret1;
    }
    TreeNode ret2 = find(root.right,val);
    if(ret2 != null) {
        return ret2;
    }
    return null;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.6 二叉树相关oj题

1. 检查两颗树是否相同（时间复杂度O(min（n，m））

做题逻辑（先看根节点，然后看左右子树）

1. 就以根节点 为基础
   先判断 两个树的根节点 进行对比
2. 如果两个根节点 没问题
   那么就看 这个根节点的 左右子树 和另一个根节点的左右子树是不是有问题
   

原题链接

return false的情况

1. 一空一不空 || 两个值不同

return true

1. 两个都为空

递归在于 return 递归函数

public boolean isSameTree(TreeNode p, TreeNode q) {
    //这里只是判断的 一个为空 一个不为空的情况 。
    // 你没有判断 两个都是空 和 两个都不是空的情况
    if(p == null && q != null || p != null && q == null) {
        return false;
    }

    if(p == null && q == null) {
        return true;
    }

    if(p.val != q.val) {
        return false;
    }

    //p != null && q != null && p.val == q.val
    return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2. 另一颗树的子树（时间复杂度：O(n*m)）

原题链接

    public boolean isSameTree(TreeNode p, TreeNode q) {
        //这里只是判断的 一个为空 一个不为空的情况 。
        // 你没有判断 两个都是空 和 两个都不是空的情况
        if(p == null && q != null || p != null && q == null) {
            return false;
        }

        if(p == null && q == null) {
            return true;
        }

        if(p.val != q.val) {
            return false;
        }

        //p != null && q != null && p.val == q.val
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
    //时间复杂度：O(n*m) 假设root这棵树的节点个数n   subRoot节点个数是m
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null) return false;

        if(isSameTree(root,subRoot)) return true;

        if(isSubtree(root.left,subRoot)) return true;

        if(isSubtree(root.right,subRoot)) return true;

        return false;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

逻辑：1. 如果树为空 不可能有子树 return flase

if(root == null) return false;
1

2. 如果 根 与 子树 正好相等 return true

if(isSameTree(root,subRoot)) return true;
1

3. 如果 根的左 与 子树正好相等 return true

if(isSubtree(root.left,subRoot)) return true;
1

4. 如果 根的右 与 子树正好相等 return true

if(isSubtree(root.right,subRoot)) return true;
1

5. if 都没有满足 那么 return false

注意：其实代码在 递归过程中，不仅仅是比较了 根的左和右，（如果没有想要的）还比较的其余的根的左右

原因：代码在递归的过程中，走遍了每个根节点

3. 二叉树最大深度

原题链接

public int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftHeight = maxDepth(root.left);
    int rightHeight = maxDepth(root.right);
    return Math.max(leftHeight, rightHeight) + 1;
}
1
2
3
4
5
6
7
8

4. 判断一棵树 是否为 平衡二叉树（时间复杂度：O(N^2)）

原题链接

1. *****不用管递归的逻辑，只需根据最上边根节点写出代码即可

    //时间复杂度：O(N^2)
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return Math.abs(leftHeight-rightHeight) <= 1
                && isBalanced(root.left)
                && isBalanced(root.right);
    }
1
2
3
4
5
6
7
8
9

2. 优化，当出现不平衡情况，便不再进行递归，而是依次return -1

优化时候的思考角度，便是从下往上思考

    //这个题 是字节考过的原题 O(n)
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        int leftTree = maxDepth(root.left);
        int rightTree = maxDepth(root.right);

        if(leftTree >= 0 && rightTree >= 0 && Math.abs(leftTree - rightTree) <= 1) {
            return Math.max(leftTree,rightTree) + 1;
        }else {
            return -1;
        }
    }

    public boolean isBalanced2(TreeNode root) {
        if(root == null) return true;
        return maxDepth(root) >= 0;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

5. 判断一棵树是否为 对称树

原题链接

***** 需要再写一个 两个参数的递归函数

    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }

        return isSymmetricChild(root.left,root.right);
    }

    private boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree) {
        if(leftTree == null && rightTree != null || leftTree != null && rightTree == null)   {
            return false;
        }

        if(leftTree == null && rightTree == null) {
            return true;
        }

        if(leftTree.val != rightTree.val) {
            return false;
        }

        return isSymmetricChild(leftTree.left,rightTree.right) &&
                isSymmetricChild(leftTree.right,rightTree.left);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

6. 二叉树的 层序遍历（队列实现，不是递归）

原题链接

    //层序遍历
    void levelOrder(TreeNode root) {
        if(root == null) return;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val+" ");
            if(cur.left != null) {
                queue.offer(cur.left);
            }
            if(cur.right != null) {
                queue.offer(cur.right);
            }
        }
        System.out.println();
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

层序遍历 到 二维数组 （二叉树的侧视图）

    /**
     * 层序遍历
     * @param root
     * @return
     */
public List<List<Integer>> levelOrder2(TreeNode root) {
    //还是依赖于队列
    List<List<Integer>> ret = new ArrayList<>();
    if(root == null) return ret;

    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        int size = queue.size();//4
        List<Integer> row = new ArrayList<>();
        while (size > 0) {
            TreeNode cur = queue.poll();
            size--;//0
            //System.out.print(cur.val + " ");
            row.add(cur.val);
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        ret.add(row);
    }
    return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

7. （视频讲解）判断一棵树 是否为 完全二叉树

注意：队列中 元素也可以是 null

    // 判断一棵树是不是完全二叉树
    boolean isCompleteTree(TreeNode root) {
        if(root == null) return true;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if(cur != null) {
                queue.offer(cur.left);
                queue.offer(cur.right);
            }else {
                break;
            }
        }

        while (!queue.isEmpty()) {
            TreeNode cur = queue.peek();
            if(cur != null) {
                //不是满二叉树
                return false;
            }else {
                queue.poll();
            }
        }
        return true;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

8. ***根据前序字符串 构建 二叉树

原题链接

import java.util.Scanner;

public class Main {
    
    class TreeNode {
        public char val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(char val) {
            this.val = val;
        }
    }
    
    public  int i = 0;//不建议定义静态的成员变量 
    
    public  TreeNode createTree(String s) {
        TreeNode root = null;
        if(s.charAt(i) != '#') {
            root = new TreeNode(s.charAt(i));
            i++;
            root.left = createTree(s);
            root.right = createTree(s);
        } else {
            i++;
        }
        return root;
    }
    
    public  void inorder(TreeNode root) {
        if(root == null) return;
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        while(scan.hasNextLine()) {
            String s = scan.nextLine();
            Main m = new Main();
            TreeNode root = m.createTree(s);
            m.inorder(root);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

1. 递归构建树— 字符串中有 ‘#’

2. 递归中，就是依次往左的

            i++;
            root.left = createTree(s);
            root.right = createTree(s);
1
2
3

也就是构造树的过程中
不用担心如何保证，节点依次是按着左边 构建的
因为递归可以保证，构建是依次按着左边去的
然后当左边的递归结束，右边的递归开始，并且是依次从下往上的了（这就是递归的规则！！）

本题的一个递归 特殊点在于 角标在递归函数外

9. ***一棵树的两个节点的 公共祖先

原题链接

方法1：子问题递归法（在root中递归获得 左右子树情况）

//最近公共祖先
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null) {
        return null;
    }
    if(root == p || root == q) {
        return root;
    }
    TreeNode retLeft = lowestCommonAncestor(root.left,p,q);
    TreeNode retRight = lowestCommonAncestor(root.right,p,q);
    if(retLeft != null && retRight != null) {
        return root;
    }else if(retLeft != null) {
        return retLeft;
    }else{
        return retRight;
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

方法2： 栈存放 路径

***一侧依次遍历，然后从下到上 左右再全部遍历 往上

public TreeNode lowestCommonAncestor2(TreeNode root,
                                      TreeNode p, TreeNode q) {
    if(root == null || p == null || q == null) {
        return null;
    }
    Stack<TreeNode> stack1 = new Stack<>();
    getPath(root,p,stack1);

    Stack<TreeNode> stack2 = new Stack<>();
    getPath(root,q,stack2);

    int size1 = stack1.size();
    int size2 = stack2.size();

    if(size1 > size2) {
        int tmp = size1-size2;
        while (tmp != 0) {
            stack1.pop();
            tmp--;
        }
    }else {
        int tmp = size2-size1;
        while (tmp != 0) {
            stack2.pop();
            tmp--;
        }
    }
private boolean getPath(TreeNode root, TreeNode node,
                        Stack<TreeNode> stack) {
    if(root == null || node == null) {
        return false;
    }
    stack.push(root);
    if(root == node) {
        return true;
    }
    boolean ret1 = getPath(root.left,node,stack);
    //不能判断false的问题，因为此时只能证明左边不存在
    if(ret1) {
        return true;
    }
    boolean ret2 = getPath(root.right,node,stack);
    if(ret2) {
        return true;
    }
    // 根节点不是  跟的左边没找到  根的右边没找到
    stack.pop();
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

10. 平衡二叉树 转换成 双向链表

*****中序遍历后 递归的回溯

原题链接

import java.util.*;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public TreeNode prev = null;
public void ConvertChild(TreeNode root) {
    if(root == null) return;
    ConvertChild(root.left);
    //System.out.print(root.val+" ");
    root.left = prev;
    if(prev != null) {
        prev.right = root;
    }
    prev = root;
    ConvertChild(root.right);
}

public TreeNode Convert(TreeNode pRootOfTree) {
    if(pRootOfTree == null) return null;

    ConvertChild(pRootOfTree);

    TreeNode head = pRootOfTree;
    while(head.left != null) {
        head = head.left;
    }
    return head;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

11. （有视频）前序 中序 创建二叉树

原题链接

public int preIndex = 0;
private TreeNode buildTreeChild(int[] preorder,int[] inorder,int inbegin,int inend) {
    //没有了左树  或者 没有了右树
    if(inbegin > inend) {
        return null;
    }
    TreeNode root = new TreeNode( preorder[preIndex]);
    //找到当前根节点 在中序遍历中的位置
    int rootIndex = findInorderIndex(inorder, preorder[preIndex],inbegin,inend);
    preIndex++;

    root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);

    root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);

    return root;

}

private int findInorderIndex(int[] inorder,int val,int inbegin,int inend) {
    for(int i = inbegin;i <= inend;i++) {
        if(inorder[i] == val) {
            return i;
        }
    }
    return -1;
}

public TreeNode buildTree(int[] preorder, int[] inorder) {

    return buildTreeChild(preorder,inorder,0,inorder.length-1);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

1. 递归函数的参数

1. 前序遍历数组，后序遍历数组
2. 后序遍历的 分界角标

2. 每次递归的作用：创建当前节点（前序）构建左右节点（后序）返回当前节点

    TreeNode root = new TreeNode( preorder[preIndex]);
    //找到当前根节点 在中序遍历中的位置
    int rootIndex = findInorderIndex(inorder, preorder[preIndex],inbegin,inend);
    preIndex++;

    root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);

    root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);

    return root;
1
2
3
4
5
6
7
8
9
10

3. 先构建左树，后构建右树（前序先 遍历到左树）

    root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);

    root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);
1
2
3

12. 后序 中序 创建二叉树

原题链接

原理：
后序遍历（左-右-根）那么就是根据从后往前找，依次是根节点，然后利用中序遍历分出左右树。
和上一题的差别就是，前序遍历是从前往后分别是根，后序遍历是从后往前依次是根

    public int postIndex = 0;//在函数中已经修改成后序遍历的数组长度

    private TreeNode buildTreeChild(int[] postorder,int[] inorder,int inbegin,int inend) {
        //没有了左树  或者 没有了右树
        if(inbegin > inend) {
            return null;
        }
        TreeNode root = new TreeNode( postorder[postIndex]);
        //找到当前根节点 在中序遍历中的位置
        int rootIndex = findInorderIndex(inorder, postorder[postIndex],inbegin,inend);
        postIndex--;
        root.right = buildTreeChild(postorder,inorder,rootIndex+1,inend);
        root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);
        return root;
    }

    private int findInorderIndex(int[] inorder,int val,int inbegin,int inend) {
        for(int i = inbegin;i <= inend;i++) {
            if(inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = postorder.length-1;
        return buildTreeChild(postorder,inorder,0,inorder.length-1);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

13. （有视频）前序遍历二叉树 转成 字符串

原题链接

public String tree2str(TreeNode root) {
    StringBuilder sb = new StringBuilder();
    tree2strChild(root,sb);
    return sb.toString();
}

private void tree2strChild(TreeNode t,StringBuilder sb) {
    if(t == null) return ;
    sb.append(t.val);

    if(t.left != null) {
        sb.append("(");
        tree2strChild(t.left,sb);
        sb.append(")");
    }else {
        if(t.right == null) {
            return;
        }else{
           sb.append("()");
        }
    }

    if(t.right == null) {
        return;
    }else{
        sb.append("(");
        tree2strChild(t.right,sb);
        sb.append(")");
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

14. 前序遍历

1. 简单递归

    void preOrder(TreeNode root) {
        if(root == null) return;
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }
1
2
3
4
5
6

2. 递归放入List数组中 addAll

	public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        ret.add(root.val);
        List<Integer> leftTree = preorderTraversal(root.left);
        ret.addAll(leftTree);

        List<Integer> rightTree = preorderTraversal(root.right);
        ret.addAll(rightTree);

        return ret;
1
2
3
4
5
6
7
8
9
10
11

3. 非递归实现 前序遍历

    public  void preorderTraversalNor(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;

        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                System.out.print(cur.val + " ");
                cur = cur.left;
            }

            TreeNode top = stack.pop();
            cur = top.right;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

15. 中序遍历

1. 普通递归实现

    void inOrder(TreeNode root) {
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }
1
2
3
4
5
6

2. 递归放入List数组中 addAll

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        List<Integer> leftTree = inorderTraversal(root.left);
        ret.addAll(leftTree);

        ret.add(root.val);

        List<Integer> rightTree = inorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;
    }
1
2
3
4
5
6
7
8
9
10
11
12

3. 非递归实现

    public void inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14

16. 后序遍历

1. 普通递归实现

    void postOrder(TreeNode root) {
        if(root == null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }
1
2
3
4
5
6

2. 递归放入数组中

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        List<Integer> leftTree = postorderTraversal(root.left);
        ret.addAll(leftTree);


        List<Integer> rightTree = postorderTraversal(root.right);
        ret.addAll(rightTree);

        ret.add(root.val);

        return ret;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3. 非递归实现 后序遍历

*****（回溯）深入子层 做标记，然后在回溯 父层 再次通过子层 做判断

    public void postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode prev = null;
        TreeNode cur = root;
        while (cur != null || !stack.empty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            //top.right 如果已经被访问了 也要弹出top所指向的节点
            if (top.right == null || top.right == prev) {
                stack.pop();
                System.out.print(top.val + " ");
                prev = top;
            } else {
                cur = top.right;
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20