-
2022春季数据结构期末考试总结
Table of contents
- 判断题
- 单选题
- 1.有组记录的排序码为{33,65,74,26,49,12,50,86},则利用堆排序的方法建立的初始堆(大顶堆)为( )
- 2.已知普通表达式`c/(e-f)*(a+b)`,对应的后缀表达式是( )
- 3.排序算法的效率,选择排序的时间复杂度为▁▁▁▁▁ 。
- 4.一棵完全二叉树上有2020个结点,其中度为2的结点的个数是( )
- 5.可以用( )定义一个完整的数据结构。
- 6.设数组 S[ ]={93, 946, 372, 9, 146, 151, 301, 485, 236, 327, 43, 892},采用最低位优先(LSD)基数排序将 S 排列成升序序列。第 1 趟分配、收集后,元素 372 之前、之后紧邻的元素分别是:
- 7.向一个有150个元素的顺序表中插入一个新元素并保持原来顺序不变,平均要移动元素的次数为( )。
- 8.假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[6,5]=( )。
- 9.若栈采用顺序存储方式存储,现两栈共享空间V[1..m],top[i]代表第i个栈( i =1,2)栈顶元素所在的下标,栈1的底在v[1],栈2的底在V[m],则栈满的条件是( )。
- 10.使用 Dijkstra 算法求下图中从顶点 1 到其余各顶点的最短路径,将当前找到的从顶点 1 到顶点 2、3、4、5 的最短路径长度保存在数组 dist 中,求出第二条最短路径后,dist 中的内容更新为:
- 11.设主串 T = `abaabaabcabaabc`,模式串 S = `abaabc`,采用 KMP 算法进行模式匹配,到匹配成功时为止,在匹配过程中进行的单个字符间的比较次数是:
- 12.下图为一个AOV网,其可能的拓扑有序序列为:
- 知识点
判断题
1.无向连通图至少有一个顶点的度为1。
T F 解析:如三个顶点三条边连成一个三角形的图每个顶点度为2
- 无向图只有连通图,有向图只有强连通图。
- 任一顶点出发进行一次深度优先搜索可访问所有顶点,说明任意两个结点连通,为连通图。
2.采用递归方式对顺序表进行快速排序,每次划分后,先处理较短的分区可以减少递归次数。
T F 解析:递归次数,取决于递归树,而递归树取决于轴枢的选择。树越平衡,递归次数越少。而对分区的长短处理顺序,影响的是递归时对栈的使用内存,而不是递归次数。
3.在散列表中,所谓同义词就是被不同散列函数映射到同一地址的两个元素。
T F 解析:映射到同一散列地址的关键字称为同义词。
4.对N个记录进行堆排序,需要的额外空间为O(N)。
T F 解析:堆排序仅需一个记录大小供交换用的辅助存储空间,所以空间复杂度为 O ( 1 ) O(1) O(1)
5.如果 e 是有权无向图 G 唯一的一条最短边,那么边 e 一定会在该图的最小生成树上。
T F 解析:给定带权无向连通图G,任意一条边e∈G且有e为G中权值最小的边(或之一),则存在一个G的最小生成树G’使e∈G’。这个命题是真的。证明可以直接借用Kruskal算法的正确性,因为选取某个权值最小边的操作正是Kruskal算法的第一步操作,你爱挑哪个都行,所以一定存在一个最小生成树包含某个最小边。
6.Prim 算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树。
T F 解析:
- prim算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树
- Kruskal 算法是维护一个森林,每一步把两棵树合并成一棵
单选题
1.有组记录的排序码为{33,65,74,26,49,12,50,86},则利用堆排序的方法建立的初始堆(大顶堆)为( )
选项 A 86,65,74,33,49,12,50,26 B 86,74,65,49,33,12,50,26 C 12,26,65,33,49,74,86,50 D 12,26,33,65,49,74,50,86 解释:如果堆的有序状态因为某个节点变得比它的父节点更大而打破,那么就需要通过交换它和它的父节点来修复堆。从最后一个非叶结点逐渐往上浮,直到有序。
2.已知普通表达式
c/(e-f)*(a+b),对应的后缀表达式是( )选项 A ef-c/ab+*B c/e-f*a+bC cef-/ab+*D cef/-ab*+解释:
给出一个中缀表达式:c/(e-f)*(a+b)
第一步:按照运算符的优先级对所有的运算单位加括号:式子变成了:((c/(e-f))*(a+b))
第二步:转换前缀与后缀表达式
前缀:把运算符号移动到对应的括号前面
则变成了:*(/(c-(ef))+(ab))
把括号去掉:*/c-ef+ab前缀式子出现
后缀:把运算符号移动到对应的括号后面
则变成了:((c(ef)-)/(ab)+)*
把括号去掉:cef-/ab+*后缀式子出现
3.排序算法的效率,选择排序的时间复杂度为▁▁▁▁▁ 。
选项 A O ( n n ) O(n\sqrt{n}) O(nn) B O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2n) C O ( n 2 ) O(n^{2}) O(n2) D O ( 2 n ) O(2^n) O(2n) 解释:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法(比如序列[5, 5, 3]第一次就将第一个[5]与[3]交换,导致第一个5挪动到第二个5后面)其实选择排序是非常简单的,和冒泡排序有异曲同工之妙。就是把元素分成两部分,一部分是有序的,另外一部分是无序的;每次循环从无序的元素中选取一个元素放到有序的元素中,依次循环到最后把所有元素都放到了有序那一部分中(也就是无序部分,元素为零);即两层循环, 所以选择排序和冒泡排序的最优的时间复杂度 和最差的时间复杂度 和平均时间复杂度 都为 : O ( n 2 ) O(n^{2}) O(n2)。
4.一棵完全二叉树上有2020个结点,其中度为2的结点的个数是( )
选项 A 1010 B 1011 C 以上都错 D 1009 解释:
一个具有n个节点的完全二叉树,其叶子节点的个数n0为: ⌈ n 2 ⌉ \left \lceil \frac{n}{2} \right \rceil ⌈2n⌉向上取整,或 ⌊ n + 1 2 ⌋ \left \lfloor \frac{n+1}{2} \right \rfloor ⌊2n+1⌋ 向下取整
度为1的节点的个数n1为:当n为偶数:1;当n为奇数:0
度为2的节点数为: ⌈ n 2 ⌉ − 1 \left \lceil \frac{n}{2} \right \rceil - 1 ⌈2n⌉−1向上取整,或 ⌊ n + 1 2 ⌋ − 1 \left \lfloor \frac{n+1}{2} \right \rfloor - 1 ⌊2n+1⌋−1 向下取整
5.可以用( )定义一个完整的数据结构。
选项 A 抽象数据类型 B 数据关系 C 数据对象 D 数据元素 解释:
数据结构包括三方面的内容:逻辑结构、存储结构、数据的运算。一个算法的设计(定义)取决于所选定的逻辑结构,而算法的实现依赖于所采用的存储结构。
抽象数据类型不关心存储结构,只描述数据的逻辑结构和抽象运算。
所以,它虽然不能实现一个数据结构,但可以定义一个数据结构。
6.设数组 S[ ]={93, 946, 372, 9, 146, 151, 301, 485, 236, 327, 43, 892},采用最低位优先(LSD)基数排序将 S 排列成升序序列。第 1 趟分配、收集后,元素 372 之前、之后紧邻的元素分别是:
选项 A 236,301 B 301,892 C 485,301 D 43,892 解释:
基数排序是一种稳定的排序方法。由于采用最低位优先(LSD) 的基数排序,即第1趟对个位进行分配和收集的操作,因此第一-趟 分配和收集后的结果是{151, 301, 372, 892, 93, 43,485, 946, 146, 236, 327,9},元素372之前、之后紧邻的元素分别是301和892,故选C。
7.向一个有150个元素的顺序表中插入一个新元素并保持原来顺序不变,平均要移动元素的次数为( )。
选项 A 75 B 0 C 149 D 150 解释:
共有n+1个插入位置, 总移动次数为 ( 1 + n ) ∗ n 2 \frac{(1+n)*n}{2} 2(1+n)∗n, 平均移动次数为 [ ( 1 + n ) ∗ n 2 ] n + 1 = n 2 \frac{\left [ \frac{(1+n)*n}{2} \right ]}{n + 1} = \frac{n}{2} n+1[2(1+n)∗n]=2n
8.假设以行序为主序存储二维数组A=array[1…100,1…100],设每个数据元素占2个存储单元,基地址为10,则LOC[6,5]=( )。
选项 A 1020 B 820 C 818 D 1018 解释:
L O C [ 6 , 5 ] = 10 + ( ( 6 − 1 ) ∗ 100 + 5 − 1 ) ∗ 2 = 1018 LOC[6,5]=10+((6 - 1) * 100 + 5 - 1) * 2 = 1018 LOC[6,5]=10+((6−1)∗100+5−1)∗2=1018
将 A A A转化 A m n A_{mn} Amn, L O C [ 6 , 5 ] = L O C [ i , j ] LOC[6,5]=LOC[i,j] LOC[6,5]=LOC[i,j]
则 L O C [ i , j ] = 基 地 址 + ( ( i − 1 ) ) ∗ n + j − 1 ) ∗ 2 LOC[i,j]=基地址+((i-1))*n+j-1)*2 LOC[i,j]=基地址+((i−1))∗n+j−1)∗2
9.若栈采用顺序存储方式存储,现两栈共享空间V[1…m],top[i]代表第i个栈( i =1,2)栈顶元素所在的下标,栈1的底在v[1],栈2的底在V[m],则栈满的条件是( )。
选项 A top[1]=top[2] B top[1]+1=top[2] C |top[2]-top[1]|=0 D top[1]+top[2]=m 解释:当两个栈的指针相邻时栈满,而非两个指针指向同一个位置,因为指向同一个位置会导致数据覆盖。
10.使用 Dijkstra 算法求下图中从顶点 1 到其余各顶点的最短路径,将当前找到的从顶点 1 到顶点 2、3、4、5 的最短路径长度保存在数组 dist 中,求出第二条最短路径后,dist 中的内容更新为:

选项 A 15、3、14、6 B 26、3、14、6 C 21、3、14、6 D 25、3、14、6 解释:

Dijkstra算法求最短路问题:
最短路径:当图是带权图时,把从一个顶点到图中其余任意一个顶点的一条路径(可能不止一条)所经过边上的权值之和,定义为该路径的带权路径长度 。把带权路径长度最短的那条路径称为最短路径。Dijkstra算法从点a到其他各个顶点的最短路径:
- 第一步:把起点a加入顶点集中,计算a到其他各点的最短路径长度,没有路径的用∞表示。比如b对应的“2 , a”表示:目前b到a的最短路径长度是2,b的前导节点是a。
- 第二步:选择上一步中路径长度最短的顶点(b)加入到顶点集中,然后更新目前a到其他各个顶点最短路径,
比如上一步中a到c的路径长度为5,加入顶点b后,由a到b再到c的路径长度为3,所以把上一步的“5,a”更新为“3,b”,表示c到a的最短路径长度为3,c的前导节点为b。
路径长度会一次增加,dist路径的长度为顶点集的个数 - 重复步骤二的方法,每次选择上一步路径长度最短的节点加入顶点集中,然后更新a到其他各个顶点最短路径,直到顶点集中包含所有顶点为止。
11.设主串 T =
abaabaabcabaabc,模式串 S =abaabc,采用 KMP 算法进行模式匹配,到匹配成功时为止,在匹配过程中进行的单个字符间的比较次数是:选项 A 15 B 10 C 12 D 9 解释:KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。

已知a和c不匹配时,前面五个字符是匹配的。查表可知,最后一个匹配字符对应的部分匹配值为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 5 − 2 = 3 5-2=3 5−2=3,所以将搜索词向后移动3位。单个字符间的比较次数为6次。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 6 - 0,再将搜索词向后移动6位,这里就不再重复了。单个字符间的比较次数为4次。不了解的看这里👉字符串匹配的KMP算法
12.下图为一个AOV网,其可能的拓扑有序序列为:
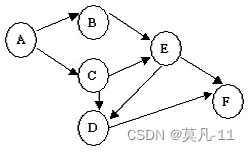
选项 A ABCDFE B ABCEDF C ABCEFD D ACBDEF 解释:
拓扑排序只适用于有向图,判断有没有环、排序任务或者上课的顺序。
拓扑排序的步骤:
1.在有向图中选一个没有前驱的顶点且输出之
2.从图中删除该顶点和所有以它为尾的弧
重复上述两步,直至全部顶点均已输出,或者当前图中不存在无前驱的顶点为止。在拓扑排序算法中,使用堆栈和使用队列产生的结果可能不同,也可能相同。
知识点
- 数据结构概念包括数据之间的逻辑结构、数据在计算机中的存储方式和数据的运算三个方面。
- 二叉搜索树查找时的结点值比较序列就是从根结点开始比较。
- 哈夫曼树的定义是构造一棵最短的带权路径树,所以这种树为最优二叉树。最优二叉树的度只有0或者2。
- 对于任意一棵高度为 5 且有 10 个结点的二叉树,若采用顺序存储结构保存,每个结点占 1 个存储单元(仅存放结点的数据信息),则存放该二叉树需要的存储单元的数量至少是多少?
因为采用顺序存储,先分配存储空间,按照满二叉树的分配,要2的k次方-1个存储单元(k是层数) - 循环队列是指用数组表示的队列,利用求余数运算使得头尾相接
- 有向完全图有n个点,那么弧有n * (n - 1)条
- 对于有向图,其邻接矩阵表示相比邻接表表示更易于进行的操作为 求一个顶点的度。
因为邻接矩阵用空间换取时间,对于查询度会比邻接表更快,因为邻接表查入度时候需要遍历所有节点 - 有向图的邻接矩阵可以是对称的,也可以是不对称的
- 如果是无向图,顶点的度数之和是边数的两倍,这是没问题的,无向图中不讲入度和出度这两个概念。
有向图中,任意一条边AB(A->B)都会给A提供一个出度,给B提供一个入度,所以
顶点的度之和 = 2 * 顶点入度之和 = 2*顶点出度之和 = 顶点入度之和+顶点出度之和=边数的两倍。 - 判断一个有向图是否存在回路
- 利用拓扑排序算法,在拓扑排序算法结束后,如果还有顶点没有输出,则说明剩下这些结点都还有前驱,则它们构成一个有向回路
- 设有向图具有n个顶点,若该图的边数e≥n,则该图一定有一个闭合的环
- 设有向图具有n个顶点,若该图的每个顶点的出度至少为1,入度也至少为1,则图中一定有回路
- 利用深度优先遍历算法,如果从有向图上的某个顶点v出发进行深度优先遍历,若在算法结束之前出现一条从顶点u到顶点v的回路,因u在生产树上是v的子孙,则图中必定存在包含顶点v和顶点u的环
- 图的基本遍历算法两种:深度遍历和广度遍历
遍历方式分为递归和非递归两种实现方式
图的遍历:就是依次访问所有的结点,且不能重复访问某个结点,且要避免死循环,所以应该把访问过的结点加上标记。
有向图和无向图都可以进行遍历操作
图的遍历算法可以执行在有回路的图中 - 强连通分量(SCC)的求法:
在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
有向图中的极大强连通子图称做有向图的强连通分量。
求强连通分量个数的前提,你需要先知道深度优先搜索(DFS)。
通过遍历每个节点,看是否有路径能够回来,如果不能回来就自成一个强连通分量。
如果形成连通图的话,那么这一条路径上的节点就形成了一个强连通分量。 - 完全无向图中,e = n * (n - 1) / 2(e表示边,n表示节点)。那么这个时候加上一个不连通的顶点就能构成一个非连通无向图。
- 判断是否会产生回路的方法为:
在初始状态下给每个顶点赋予不同的标记,对于遍历过程的每条边,其都有两个顶点,判断这两个顶点的标记是否一致,如果一致,说明它们本身就处在一棵树中,如果继续连接就会产生回路;如果不一致,说明它们之间还没有任何关系,可以连接。 - 若使用 AOE 网估算工程进度,关键路径是从源点到汇点路径长度最长的路径。
- 一个有n个顶点的简单有向图最多有 n(n - 1)条边
有n个顶点的强连通图最多有n(n-1)条边,最少有n条边。 - 一个无向图 G = ( V , E ) 是连通的,那么边的数目大于等于顶点的数目减一:∣ E ∣ > = ∣ V ∣ − 1,而反之不成立
- 简单选择排序最坏情况下,每趟都交换元素,因为排序共 n-1 趟。
- 在快速排序的一趟划分过程中,当遇到与基准主元相等的元素时,如果左右指针都会停止移动,那么当所有元素都相等时,算法的时间复杂度是O(nlogn)
原因:指针停止就会不断交换左右指针的元素,这样虽然多余的交换次数变多,但让子序列的元素相对平均,所以一共有logN次划分,每次时间复杂度是O(N)。
-
相关阅读:
非零基础自学Java (老师:韩顺平) 第11章 枚举和注解 【1 枚举】
WPF 附加属性+控件模板,完成自定义控件。建议观看HandyControl源码
ACWing每日一题.3511
【考研系列】-二战在家复习经历
DP108T国产高集成度USB/YTPE-C音频声卡芯片SSOP24
调试记录 单片机GD32F103C8T6(兆易创新) 程序烧写完成但是没有现象 (自己做的板子)
.NET、VUE利用RSA加密完成登录并且发放JWT令牌设置权限访问
带你了解基于Ploto构建自动驾驶平台
基于Java的家政公司服务平台设计与实现(源码+lw+部署文档+讲解等)
一篇带你走进程序设计的准则——DAO和MVC设计模式
- 原文地址:https://blog.csdn.net/weixin_51333606/article/details/125569205