矩阵分析与应用 - 码农知识堂

矩阵分析与应用
本文学习来源是《矩阵分析与应用》

矩阵的二次型

任意一个正方矩阵A的二次型 $x^{H}Ax$ 是一个实标量，以实矩阵为例：

$x^{T}Ax =\begin{bmatrix} x_{1} ,x_{2} , x_{3} \end{bmatrix}\begin{bmatrix} 1 & 4&2 \\ -1& 7&5 \\ -1&6 & 3 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} \\ =x_{1}^{2}-x_{2}x_{1}-x_{3}x_{1}+4x_{1}x_{2}+7x_{2}^{2}+6x_{3}x_{2}+2x_{1}x_{3}+5x_{2}x_{3}+3x_{3}^{2}\\=x_{1}^{2}+7x_{2}^{2}+3x_{3}^{2}+3x_{1}x_{2}+x_{1}x_{3}+11x_{2}x_{3}$

这是变量x的二次型函数，我们称 $x^{T}Ax$ 为矩阵A的二次型。

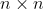推而广之，若 $x=[x_{1},x_{2},.. .,x_{n}]^{T}$ ，且 $n\times n$ 矩阵A的元素为 $a_{ij}$ ，则二次型

$x^{T}Ax=\sum_{i=1}^{n}\sum_{j=1}^{n}x_{i}x_{j}a_{ij} \\=\sum_{i=1}^{n}a_{ii} x_{i}^{2}+\sum_{i=1,i\neq j}^{n}\sum_{j=1}^{n}a_{ij}x_{i}x_{j}\\=\sum_{i=1}^{n}a_{ii} x_{i}^{2}+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(a_{ij}+a_{ji})x_{i}x_{j}$

若两个矩阵A，B满足对角线相等，且满足 $a_{ij}+a_{ji}=b_{ij}+b_{ji}$ ,则这两个矩阵的二次型就相等。

如：

$A=\begin{bmatrix} 1 & 4&2 \\ -1& 7&5 \\ -1&6 & 3 \end{bmatrix}B=\begin{bmatrix} 1 & -1&-1 \\ 4& 7&6 \\ 2&5 & 3 \end{bmatrix}C=\begin{bmatrix} 1 & 114&52\\ -111& 7&2 \\ -51&9 & 3 \end{bmatrix}$

具有相同的二次型。即：

$x^{T}Ax=x^{T}Bx=x^{T}Cx\\=x_{1}^{2}+7x_{2}^{2}+3x_{3}^{2}+3x_{1}x_{2}+x_{1}x_{3}+11x_{2}x_{3}$

即对于任何一个二次型函数

$f\left ( x_{1},x_{2},.. .,x_{n} \right )=\sum_{i=1}^{n}\alpha _{ii}x_{i}^{2}+\sum_{i=1,i \neq j}^{n}\sum_{j=1}^{n}\alpha _{ij}x_{i}x_{j}$

存在许多矩阵A，它们的二次型 $x^{T}Ax=f\left ( x_{1},x_{2},.. .,x_{n} \right )$ 相同，但是，只有一个唯一的对称矩阵A满足 $x^{T}Ax=f\left ( x_{1},x_{2},.. .,x_{n} \right )$ ，其元素为 $a_{ii}=\alpha _{ii}$ 和 $a_{ij}=a_{ji}=\frac{1}{2}(\alpha _{ij}+\alpha _{ji})$ ，其中， $i=1,2,.. .,n,j=1,2,.. .,n,i\neq j$ 。因此在讨论矩阵A的二次型时，通常都假定A为实对称矩阵或复共轭对称矩阵。

一个复共轭对称矩阵A称为：
- 正定矩阵，若二次型 $x^{H}Ax> 0,\forall x \neq 0$
- 半正定矩阵，若二次型 $x^{H}Ax\geqslant 0,\forall x \neq 0$
- 负定矩阵，若二次型 $x^{H}Ax< 0,\forall x \neq 0$
- 半负定矩阵，若二次型 $x^{H}Ax\leqslant 0,\forall x \neq 0$
- 不定矩阵，若二次型 $x^{H}Ax$ 既可能取正值，也可能取负值。
例如：实对称矩阵

$R=\begin{bmatrix} 3 & -1&0 \\ -1 & 3& -1\\ 0&-1 & 3 \end{bmatrix}$

是正定的，因为二次型 $x^{H}Rx=2x_{1}^{2}+x_{2}^{2}+2x_{3}^{2}+\left ( x_{1}-x_{2} \right )^{2}+\left ( x_{2}-x_{3} \right )^{2}> 0$ ，仅 $x_{1}=x_{2}=x_{3}=0$ 时等式为0。

这里继续学习一个非负矩阵的概念。

设矩阵 $A_{m \times n}$ 的元素为 $a_{ij}$ ，若

$a_{ij}\geqslant 0, \forall i=1,2,.. .,m,j=1,2,.. .,n$

即A的所有元素都是非负的，则称A为非负矩阵。

若A的所有元素都是正的，则称A为正矩阵。

非负矩阵和正矩阵分别用符号 $A\geqslant 0$ 和简记，以下是正定矩阵和正矩阵之间的区别：

正定矩阵一定是正方的矩阵，但是正矩阵可以是非正方的。

正定矩阵A的定义为： $x^{H}Ax> 0,\forall x \neq 0$ ，正矩阵的定义为： $a_{ij} > 0$

正定矩阵的符号为： $x^{H}Ax>0$ ,正矩阵的符号为：

矩阵的迹

n*n矩阵A的对角元素之和称为A的迹，非正方矩阵没有迹。迹记作tr(A),即：
$tr(A)=a_{11}+a_{22}+.. .+a_{nn}=\sum_{i=1}^{n}a_{ii}$

以下是关于迹的等式：
1. 若A和B均为n*n的矩阵，则 $tr(A\pm B)=tr(A) \pm tr(B)$
2. 若c是一个复常数或者实常数，则
3. 若A和B均为n*n的矩阵,且 $c_{1}$ 和 $c_{2}$ 为常数，则 $tr(c_{1}A\pm c_{2}B)=c_{1}tr(A) \pm c_{2}tr(B)$
4. 矩阵A的转置，复数共轭的迹为： $tr(A^{T})=tr(A),tr(A^{*})=[tr(A)]^{*}$
5. 若A为m*n矩阵，B为n*m矩阵，则
6. 若A，B均是一个m*m矩阵，且B非奇异，则 $tr(BAB^{-1})=tr(B^{-1}AB)=tr(A)$
7. 若A是一个m*n的矩阵，则 $tr(A^{H}A)=0\Leftrightarrow A=O_{m \times n}$
8. 迹等于特征值之和，即 $tr(A)=\lambda _{1}+\lambda _{2}+.. .+\lambda _{n}$
9. $tr(A^{k})=\sum_{i=1}^{n}\lambda _{i}^{k}$
相关阅读:
Unity --- 场景/场景管理类与异步场景加载法
 SwiftUI SQLite教程之带有历史的搜索栏List App (教程含完整代码)
【前端知识】Three 学习日志（四）—— 相机控件
 【python运维脚本实践】python实践篇之使用Python处理有序文件数据的多线程实例
 Flutter dio Http请求之Cookie管理
 82.（cesium之家）cesium点在3d模型上运动
 ChatGPT推出新“朗读”功能支持多语言与声音；使用大型语言模型增强分类数据集
 步进电机驱动板在电机运行中起到什么作用？
CPU使用率和负载区别及分析
 MyBatis一对多关联查询
原文地址：https://blog.csdn.net/weixin_46007132/article/details/125591473