• 数据结构和算法

    一、认识时间复杂度

    用大Ο记号表示算法的时间性能。  ​​​​

    二、二进制与整数之间的转换

    1、正整数与二进制互转

     除2之后将余数倒序排列， 直到商小于1

    201 / 2 = 100······1

    100 / 2 = 50  ······0

    50 / 2 = 25    ······0

    25 / 2 = 12    ······1

    12 / 2 = 6      ······0

    6 / 2 = 3        ······0

    3 / 2 = 1        ······1

    1 / 2 = 0        ······1    (商小于1，结束计算并将余数倒序排列)

    得到：201（十进制） = 11001001（二进制）

    2、负整数转二进制

    1）得到取绝对值的整数的二进制。 如 -201，先得到201的二进制11001001

    2）取反。得00110110

    3）加1。  得00110111

    3、小数部分转二进制

    1）小数部分乘2后将整数部分顺序排列。 如0.125，整数部分顺序排列得001

    2）前面加0.       得0.001

     三、排序算法

    排序算法大体可分为两种：

    • 一种是比较排序，时间复杂度O(nlogn) ~ O(n^2)，主要有：冒泡排序，选择排序，插入排序，归并排序，堆排序，快速排序等。
    • 另一种是非比较排序，时间复杂度可以达到O(n)，主要有：计数排序，基数排序，桶排序等。

    下面给出常见比较算法的排序性能

    1、交换方法

    1.     //交换位置
    2.     public static void swap(int[] arr,int i,int j){
    3.         if(arr[i] > arr[j]){
    4.             int num = arr[i];
    5.             arr[i] = arr[j];
    6.             arr[j] = num;
    7.         }
    8.     }
    9.  
    10.     //交换值
    11.     //异或交换效率快
    12.     //两个不同内存的变量（两个变量都是等与10），交换结果还是10
    13.     //两个相同内存的变量（两个变量都是等与10），交换结果就为0
    14.     public static void swap1(int[] arr,int i,int j){
    15.         /**
    16.          * 异或左边arr[i] = 甲
    17.          * 异或右边arr[j] = 已
    18.          * 等号左边arr[i] = 甲 ^ 已
    19.          */
    20.         arr[i] = arr[i] ^ arr[j];
    21.         /**
    22.          * (上面的公式得来的)异或左边arr[i] = 甲 ^ 已
    23.          * 异或右边arr[j] = 已
    24.          * 异或运算相等为0，不同为1
    25.          * 等号左边arr[j] = 甲 ^ 已 ^ 已 = 甲
    26.          */
    27.         arr[j] = arr[i] ^ arr[j];
    28.         /**
    29.          * 异或左边arr[i] = 甲 ^ 已
    30.          * (由上面第二个公式得来的)异或右边arr[j] = 甲
    31.          * 异或运算相等为0，不同为1
    32.          * 等号左边arr[i] = 甲 ^ 已 ^ 甲 = 已
    33.          */
    34.         arr[i] = arr[i] ^ arr[j];
    35.     }

    2、选择排序

    算法描述

    1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
    2. 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
    3. 重复第二步，直到所有元素均排序完毕。

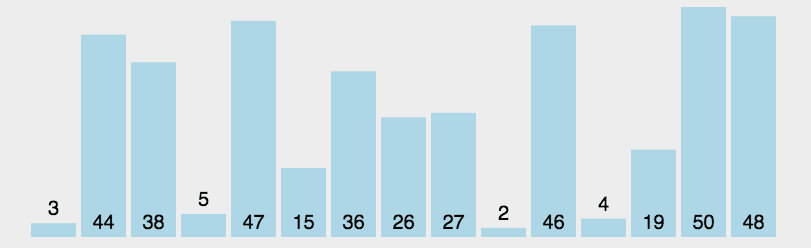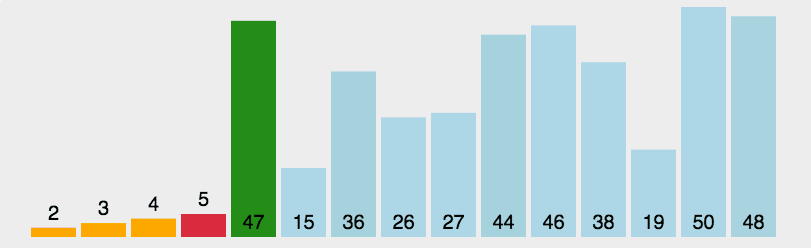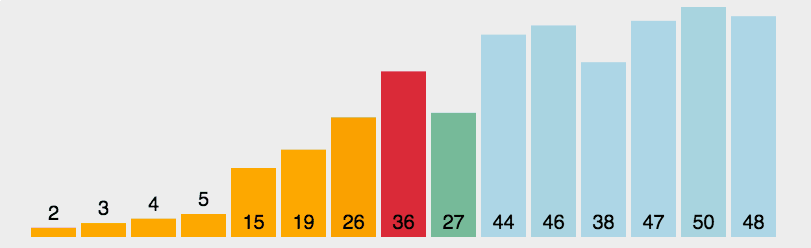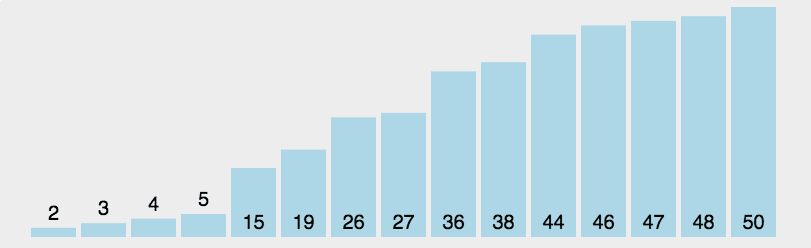
     具体代码：

    1.     //交换位置
    2.     public static void swap(int[] arr,int i,int j){
    3.         if(arr[i] > arr[j]){
    4.             int num = arr[i];
    5.             arr[i] = arr[j];
    6.             arr[j] = num;
    7.         }
    8.     }
    9.  
    10.     //选择排序
    11.     public static int[] xzpx(int[] arr){
    12.         if(arr == null || arr.length < 2){
    13.             return arr;
    14.         }
    15.  
    16.         for(int i = 0;i < arr.length;i++){
    17.             int minIndex = i;
    18.             for(int j = i + 1;j < arr.length;j++){
    19.                 if(arr[j] < arr[minIndex]){
    20.                     minIndex = j;
    21.                 }
    22.             }
    23.             swap(arr,i,minIndex);
    24.         }
    25.         return arr;
    26.     }

    3、冒泡排序 

    冒泡排序也是通过遍历比较左右值得大小，例如排升序即左值大于右值交换，最后最大值即排到最右边。（每次遍历一次都能找到最大的数）

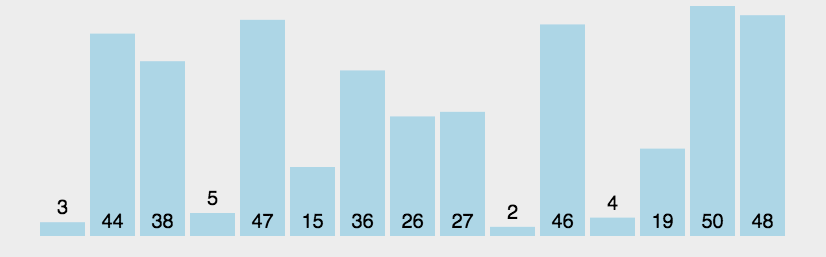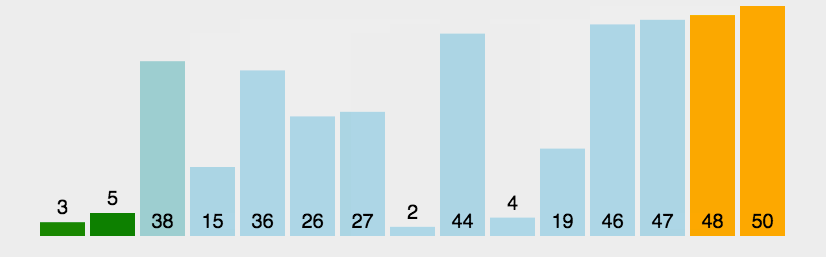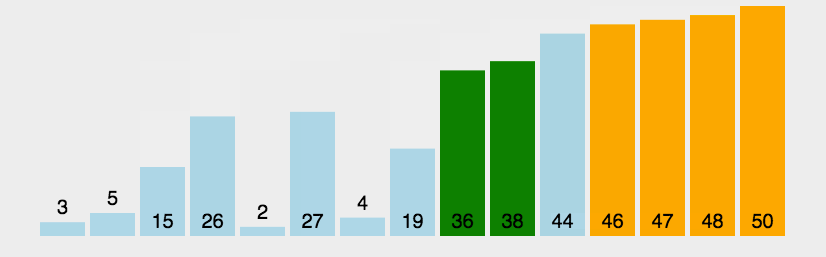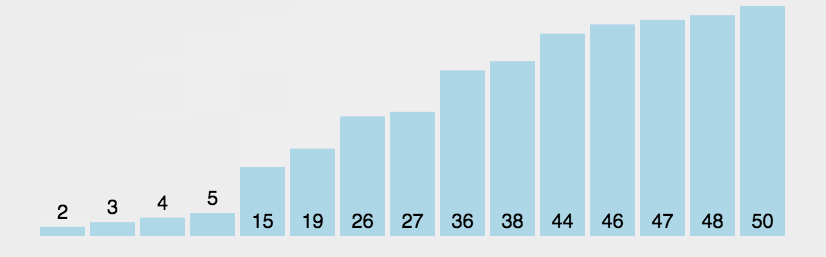
    在这里插入图片描述

     实现代码：

    1.     //交换位置
    2.     public static void swap(int[] arr,int i,int j){
    3.         if(arr[i] > arr[j]){
    4.             int num = arr[i];
    5.             arr[i] = arr[j];
    6.             arr[j] = num;
    7.         }
    8.     }
    9.  
    10.     //冒泡排序
    11.     public static int[] mppx(int[] arr){
    12.         if(arr == null || arr.length < 2){
    13.             return arr;
    14.         }
    15.  
    16.         for(int i = 0;i < arr.length;i++){
    17.             for(int j = 0;j < arr.length - i - 1;j++){
    18.                 if(arr[j] > arr[j + 1]){
    19.                     swap(arr,j,j + 1);
    20.                 }
    21.             }
    22.         }
    23.         return arr;
    24.     }

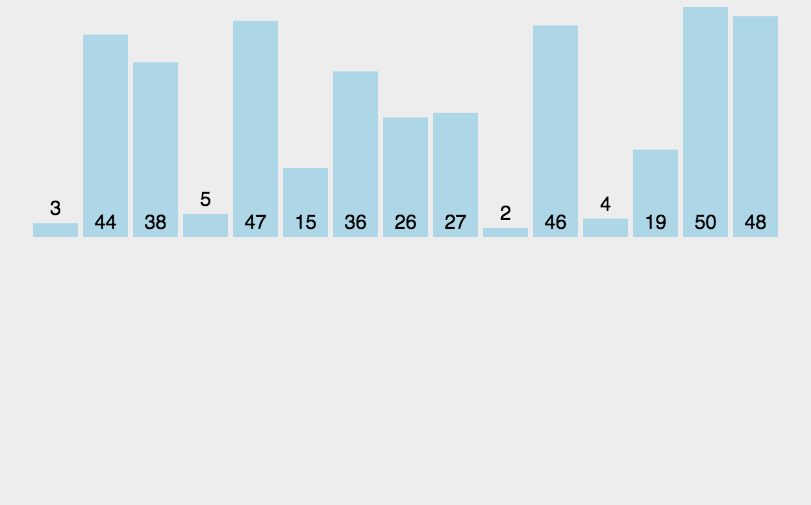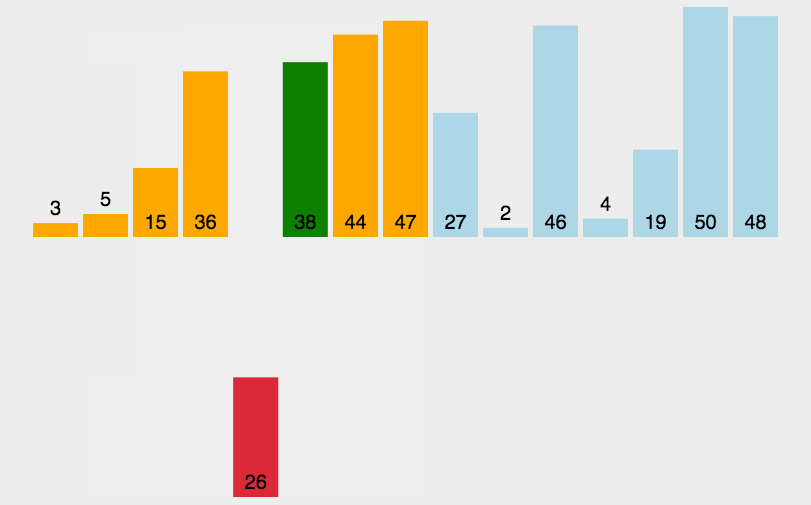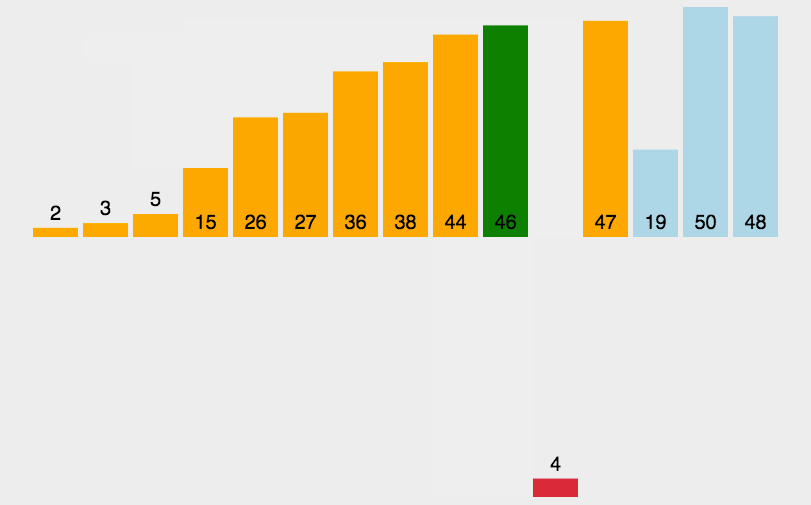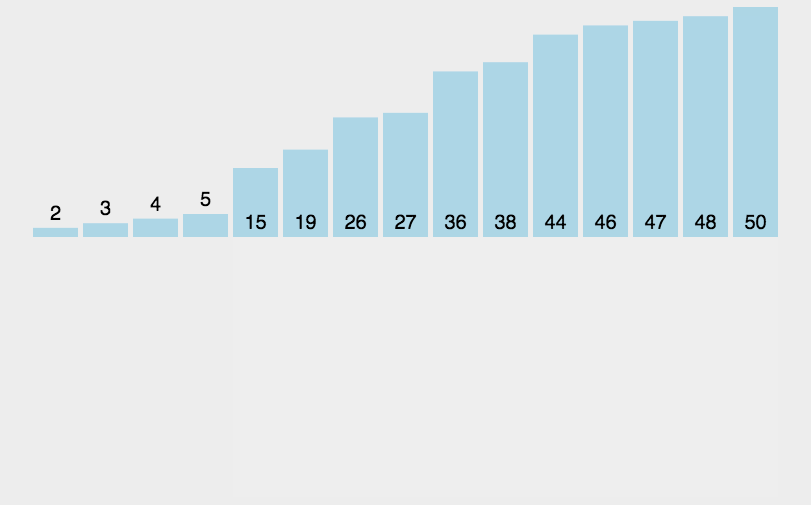
    4、插入排序 

    直接插入排序就是把待排序的元素逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。

    在这里插入图片描述

    1.     //插入排序
    2.     public static int[] crpx(int[] arr){
    3.         for(int i = 1;i < arr.length;i++){  //0 ~ i是有序数组
    4.             for(int j = i - 1;j >= 0;j--){
    5.                 if(arr[j + 1] < arr[j]){
    6.                     swap(arr,j,j + 1);
    7.                 }
    8.             }
    9.         }
    10.         return arr;
    11.     }

     5、归并排序

     

    1.     //归并排序
    2.     public static void mergeSort(int[] arr,int left,int right){
    3.         if(left == right){
    4.             return;
    5.         }
    6.  
    7.         int mid = left + ((right - left) >> 1);
    8.         //向左递归进行分解
    9.         mergeSort(arr,left,mid);
    10.         //向右递归进行分解
    11.         mergeSort(arr,mid + 1,right);
    12.         //合并
    13.         merge(arr,left,mid,right);
    14.     }
    15.  
    16.     /**
    17.      * 合并的方法（治）
    18.      * @param arr 排序的原始数组
    19.      * @param left 左边有序序列的初始索引
    20.      * @param mid 中间索引
    21.      * @param right 右边的索引
    22.      */
    23.     public static void merge(int[] arr,int left,int mid,int right){
    24.         int l = left;  //左边有序数组的左指针
    25.         int j = mid + 1; //右边有序数组的左指针
    26.         int i = 0; //指向temp数组的指针
    27.         int[] temp = new int[right - left + 1]; //用来做中转的数组
    28.         
    29.         //步骤一：
    30.         //先把左右两边（有序）的数据按照规则填充到temp数组
    31.         //直到左右两边的有序序列，有一边处理完毕为止
    32.         while(l <= mid && j <= right){
    33.             temp[i++] = arr[l] <= arr[j] ? arr[l++] : arr[j++];
    34.         }
    35.  
    36.         //如果左边还有剩余的数据就依次全部填充到temp数组中
    37.         while(l <= mid){
    38.             temp[i++] = arr[l++];
    39.         }
    40.  
    41.         //如果右边还有剩余的数据就依次全部填充到temp数组中
    42.         while(j <= right){
    43.             temp[i++] = arr[j++];
    44.         }
    45.         
    46.         步骤二：
    47.         //将temp数组的元素拷贝到arr中
    48.         //注意，并不是每次都拷贝所有
    49.         i = 0;
    50.         int m = left;
    51.         //第一次合并 m = 0,right = 1
    52.         //第二次合并 m = 2,right = 3
    53.         //第三次合并 m = 0,right = 3
    54.         //最后一次合并 m = 0,right = arr.length
    55.         while(m <= right){
    56.             arr[m++] = temp[i++];
    57.         }
    58.     }

     步骤一：图解,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]

     步骤二：图解，

     

    5.1、小和问题和逆序问题

    小和问题：

    图解：

    用暴力算法求小和（时间复杂度O(N^2)）：

    1.     //暴力解法求小和
    2.     public static int smallAnd(int[] arr){
    3.         int num = 0;
    4.         for(int i = 1;i < arr.length;i++){
    5.             for(int j = 0;j < i;j++){
    6.                 if(arr[j] < arr[i]){
    7.                     num += arr[j];
    8.                 }
    9.             }
    10.         }
    11.         return num;
    12.     }

     用递归排序来求小和（时间复杂度为O(logN)）：

    图解：

     下面的步骤缺一不可：如果把第一个方法去掉就会得出的结果就是有错误的

    1.     //用递归返回小和
    2.     public static int samllAnd(int[] arr){
    3.         if(arr == null || arr.length < 2){
    4.             return 0;
    5.         }
    6.  
    7.         return recursionSmallAnd(arr,0,arr.length - 1);
    8.     }
    9.  
    10.     //用递归排序来解决小和问题
    11.     public static int recursionSmallAnd(int[] arr,int left,int right){
    12.         if(left == right){
    13.             return 0;
    14.         }
    15.  
    16.         int mid = left + ((right - left) >> 1);
    17.  
    18.         return recursionSmallAnd(arr,left,mid) +
    19.                 recursionSmallAnd(arr,mid + 1,right) +
    20.                 mergeRecursion(arr,left,mid,right);
    21.     }
    22.  
    23.     public static int mergeRecursion(int[] arr,int left,int mid,int right){
    24.         int l = left;
    25.         int r = mid + 1;
    26.         int num = 0;
    27.         int[] temp = new int[arr.length];
    28.         int sum = 0;
    29.  
    30.         while(l <= mid && r <= right){
    31.             //(r - mid + 1):表示右边的数组有几个数是大于左边第一个下标的数
    32.             // (r - mid + 1):表示右边的数组有几个数是大于左边第二个下标的数
    33.             // (r - mid + 1):表示右边的数组有几个数是大于左边第l个下标的数
    34.             sum += arr[l] < arr[r] ? (r - mid + 1) * arr[l] : 0;
    35.             temp[num++] = arr[l] <= arr[r] ? arr[l++] : arr[r++];
    36.         }
    37.  
    38.         while(l <= mid){
    39.             temp[num++] = arr[l++];
    40.         }
    41.  
    42.         while(r <= right){
    43.             temp[num++] = arr[r++];
    44.         }
    45.  
    46.         num = 0;
    47.         int m = left;
    48.         while(m <= right){
    49.             arr[m++] = temp[num++];
    50.         }
    51.         return sum;
    52.     }

    逆序问题： 

    在一个数组中，左边的数比右边的大，则两个数构成一个逆序对，请算出总共有多少个逆序对。

    暴力求解： 

    1.     //暴力求解逆序对
    2.     public static int reversePair(int[] arr){
    3.         int number = 0;
    4.         for(int i = 0;i < arr.length - 1;i++){
    5.             for(int j = i + 1;j < arr.length;j++){
    6.                 if(arr[j] < arr[i]){
    7.                     number++;
    8.                 }
    9.             }
    10.         }
    11.         return number;
    12.     }

     归并排序求解：

    逆向思维：左边有几个数大于右边的这个数

    1.     //递归排序求解逆序对
    2.     public static int recursionReversePair(int[] arr){
    3.         if(arr == null || arr.length < 1){
    4.             return 0;
    5.         }
    6.  
    7.         return recursionSort(arr,0,arr.length - 1);
    8.     }
    9.  
    10.     //递归排序
    11.     public static int recursionSort(int[] arr,int left,int right){
    12.         if(left > right){
    13.             return 0;
    14.         }
    15.  
    16.         int median = left + ((right - left) >> 1);
    17.  
    18.         return recursionSort(arr,left,median) +
    19.                 recursionSort(arr,median + 1,right) +
    20.                 recursionMerge(arr,left,median,right);
    21.     }
    22.  
    23.     //合并方法
    24.     public static int recursionMerge(int[] arr,int left,int median,int right){
    25.         int l = left;
    26.         int r = median + 1;
    27.         int number = 0;
    28.         int[] array = new int[arr.length];
    29.         int sum = 0;
    30.  
    31.         while(l <= median && r <= right){
    32.             //左边有几个数大于右边
    33.             sum += arr[l] > arr[r] ? l + 1 : 0;
    34.             array[number++] = arr[l] <= arr[r] ? arr[l++] : arr[r++];
    35.         }
    36.  
    37.         while(l <= median){
    38.             array[number++] = arr[l++];
    39.         }
    40.  
    41.         while(r <= right){
    42.             array[number++] = arr[r++];
    43.         }
    44.  
    45.         number = 0;
    46.         int anotherNumber = left;
    47.         while(anotherNumber <= right){
    48.             arr[anotherNumber++] = array[number++];
    49.         }
    50.         return sum;
    51.     }

    6、快速排序

    下次回来继续学习：

    1. public static void quickSort(int[] arr){
    2.         if(arr == null || arr.length < 2){
    3.             return;
    4.         }
    5.         quickSort(arr,0,arr.length - 1);
    6.     }
    7.  
    8.     public static void quickSort(int[] arr,int L,int R){
    9.         if(L < R){
    10.             swap(arr,L + (int)(Math.random() * (R - L + 1)),R);
    11.             int[] p = partition(arr,L,R);
    12.             quickSort(arr,L,p[0] - 1);
    13.             quickSort(arr,p[1] + 1,R);
    14.         }
    15.     }
    16.  
    17.     public static int[] partition(int[] arr,int L,int R){
    18.         int less = L - 1;
    19.         int more = R;
    20.         while(L < more){
    21.             if (arr[L] < arr[R]) {
    22.                 swap(arr,++less,L++);
    23.             }else if(arr[L] > arr[R]){
    24.                 swap(arr,--more,L);
    25.             }else{
    26.                 L++;
    27.             }
    28.         }
    29.         swap(arr,more,R);
    30.         return new int[]{less + 1,more};
    31.     }
    32.  
    33.     public static void swap(int[] arr,int l,int r){
    34.         int number = arr[l];
    35.         arr[l] = arr[r];
    36.         arr[r] = number;
    37.     }

    7、堆排序 

    堆的性质：

    ① 是一棵完全二叉树
    ② 每个节点的值都大于或等于其子节点的值，为最大堆；反之为最小堆。

    堆储存方式：

     图二：

    四、查找算法 

    1、二分查找

    二分查找的时间复杂度为 O(log2n)。

    什么是 log2(n)

    • 表示的是 以 2 的多少次方等于 n
    • 数学上叫：以 2 为底 n 的 对数

    1.      /**
    2.      * 二分查找
    3.      * @param arr 数组
    4.      * @param left 左边的索引
    5.      * @param right 右边的索引
    6.      * @param num 要查找的数
    7.      * @return  如果找到就返回下标，如果没有找到，就返回-1
    8.      */
    9.     public static int efcz(int[] arr,int left,int right,int num){
    10.         //当left > right时，说明递归整个数组，但是没有找到
    11.         if(left > right){
    12.             return -1;
    13.         }
    14.  
    15.         int mid = (left + right) / 2;
    16.         int midVal = arr[mid];
    17.  
    18.         if(num > midVal){ //向右递归
    19.             return efcz(arr,mid + 1,right,num);
    20.         }else if(num < midVal){ //向左递归
    21.             return efcz(arr,left,mid,num);
    22.         }else{
    23.             return mid;
    24.         }
    25.     }

    改进二分查找方法，返回多个 与num元素相同的元素下标

    1.     /**
    2.      * 二分查找 （查找多个元素）
    3.      * @param arr 数组
    4.      * @param left 左边的索引
    5.      * @param right 右边的索引
    6.      * @param number 要查找的数
    7.      * @return  如果找到就返回下标，如果没有找到，就返回null
    8.      */
    9.     public static ArrayList binarySearch(int[] arr, int left, int right, int number){
    10.         //当left > right时，说明递归整个数组，但是没有找到
    11.         if(left > right){
    12.             return null;
    13.         }
    14.  
    15.         ArrayList list = new ArrayList<>();
    16.         int median = left + ((right - left) >> 1);
    17.  
    18.         if(number > arr[median]){
    19.             return binarySearch(arr,median + 1,right,number);
    20.         }else if(number < arr[median]){
    21.             return binarySearch(arr,left,median,number);
    22.         }else{
    23.             list.add(median);
    24.  
    25.             //向median索引值的左边扫描，将所有满足number的元素下标加入到ArrayList集合中
    26.             int anotherNumber = median - 1;
    27.             while(arr[anotherNumber] == number){
    28.                 list.add(anotherNumber--);
    29.             }
    30.  
    31.             //向median索引值的右边扫描，将所有满足number的元素下标加入到集合ArrayList集合中
    32.             anotherNumber = median + 1;
    33.             while(arr[anotherNumber] == number){
    34.                 list.add(anotherNumber++);
    35.             }
    36.         }
    37.         return list;
    38.     }

    2、递归方法 

    2.1、左移（<<），右移（>>）

    左移 <<：

     左移运算有乘以2的N次方的效果。一个数向左移动1位，就相当于乘以2的1次方，移动两位就相当于乘以2的2次方，也就是乘以4。位移操作在实际运算时远远快于乘法操作，所以在某些对运算速度要求非常高的场合，可以考虑用左移代替乘以2的N次方的乘法操作。

    右移 >>：

    对于正数而言，带符号右移之后产生的数字确实等于除以2的N次方；

    对于负数而言，带符号右移的效果分为两种情况：

    如果这个负数是“2的N次方”的整数倍，那么带符号右移N位的效果也等于除以2的N次方。举个例子：我们还是把N的值设为3，如果对于“-16”来说，它是“2的3次方”的整数倍，那么带符号右移3位的结果是-2，这个结果相当于“-16除以2的3次方”。

    如果这个负数不是“2的N次方”的整数倍，那么右移N位之后，是在除以2的N次方的结果之上还要减去1。比如，对于-15来说，它不是“2的3次方”的整数倍，那么带符号右移3位的结果是-2，这个运算结果其实就是“-15被2的3次方整除再减去1”。

    2.2、求最大值

    1.     //递归找最大值
    2.     public static int zdzdg(int[] arr,int left,int right){
    3.         if(left == right){
    4.             return arr[left];
    5.         }
    6.  
    7.         int mid = left + ((right - left) >> 1);
    8.         int leftMax = zdzdg(arr,left,mid);
    9.         int rightMax = zdzdg(arr,mid + 1,right);
    10.         return Math.max(leftMax,rightMax);
    11.     }

     2.3、master公式

    五、对数器

    1.     //对数器
    2.     public static int[] generateRandomArray(int maxSize,int maxValue){
    3.         //Math.random() -> [0,1) 所有的小数，等概率返回一个
    4.         //Math.random() * N -> [0,N) 所有小数，等概率返回一个
    5.         //(int)(Math.random() * N) -> [0,N-1] 所有的整数，等概率返回一个
    6.  
    7.         int[] arr = new int[(int)((maxSize + 1) * Math.random())]; //长度随机
    8.         for(int i = 0;i < arr.length;i++){
    9.             arr[i] = (int)((maxValue + 1) * Math.random()) - (int)(maxValue * Math.random());
    10.         }
    11.         return arr;
    12.     }

    五、数据结构

    1、二叉树

    完全二叉树：

    2、堆结构

  • 相关阅读:
    数据库连接池
    1740. 找到⼆叉树中的距离
    查找浏览器中保存的密码
    中秋发祝福？一套程序让你成为【相亲相爱一家人】群里最靓的仔
    手把手Java爬虫教学 - 8. 项目2 - 数据库表设计 & 爬虫代码实现
    消除注释C++
    abp(net core)+easyui+efcore实现仓储管理系统——ABP升级7.3下(五十九)
    浅谈 AI 大模型的崛起与未来展望：马斯克的 xAI 与中国产业发展
    企业如何建立全链路数字化体系，才能让卖货更容易？
    vue的由来、vue教程和M-V-VM架构思想、vue的使用、nodejs
  • 原文地址：https://blog.csdn.net/A1916403680/article/details/127202999