-
矩阵分析与应用-04-向量空间、内积空间与线性映射01
虽然许多工程问题也可以不使用线性空间进行研究,但是线性空间的使用却可以给问题的描述带来诸多的方便。本质上讲,线性空间是某--类事物在矩阵代数里的一个抽象的集合表示,线性映射或线性变换则反映线性空间中元素间最基本的线性联系,它们为线性函数的研究提供了极大的方便。可以说,线性代数就是研究线性空间和线性变换理论的数学分支。
集合的基本概念
1.与集合运算有关的几个数学符号
 表示对所有
表示对所有 表示
表示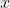 属于集合
属于集合 ,即
,即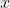 是集合
是集合 的一个元素
的一个元素 表示
表示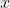 不属于集合
不属于集合 ,即
,即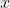 不是集合
不是集合 的一个元素
的一个元素 表示使得
表示使得 表示存在
表示存在2.集合的基本运算
 读作集合
读作集合 包含于集合
包含于集合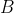 或
或 是
是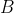 的一个子集,即
的一个子集,即 中每一个元素都是
中每一个元素都是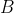 的元素。
的元素。 称
称 是
是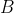 的一个真子集。符号
的一个真子集。符号 表示为
表示为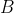 包含
包含 或
或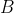 是
是 的超集。
的超集。 表示没有任何元素的集合,又称空集。
表示没有任何元素的集合,又称空集。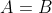 表示
表示 等于
等于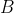 ,即
,即 和
和 ,或
,或 和
和
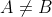 表示
表示 不属于
不属于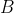 ,反过来
,反过来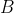 也不属于
也不属于
 表示
表示 和
和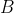 的并集
的并集 表示
表示 和
和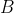 的交集
的交集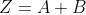 表示
表示 和
和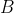 的和集
的和集 表示集合差
表示集合差 表示在
表示在 集合
集合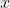 中的补集
中的补集 表示
表示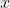 和
和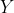 的笛卡尔积
的笛卡尔积向量空间
定义1 以向量为元素的集合V称为向量空间,若加法运算定义为两个向量之间的加法,乘法运算定义为向量与标量域S中的标量之间的乘法,并且对于向量集合V中的向量x, y, w和标量域S中的标址a1, a2,以下两个闭合性和关于加法及乘法的八个公理(axiom)[也称公设(postulate)或定律(law)]满足:
闭合性:
1.若
 和
和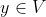 ,则
,则 ,即
,即 在加法下是闭合的,简称加法的闭合性;
在加法下是闭合的,简称加法的闭合性;2.若
 是一个标量,
是一个标量,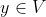 ,则
,则 ,即
,即 在标量乘法下是闭合的,简称标量乘法的闭合性。
在标量乘法下是闭合的,简称标量乘法的闭合性。加法的公理:
1.
 ,
,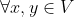 ,称为加法的交换律;
,称为加法的交换律;2.
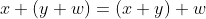 ,
, ,称为加法的结合律;
,称为加法的结合律;3.在
 中存在一个零向量
中存在一个零向量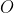 、使得对于任意向量y ∈V,恒有y+0= y(零向量的存在性)
、使得对于任意向量y ∈V,恒有y+0= y(零向量的存在性)4.给定一个向量
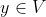 ,存在另一个向量
,存在另一个向量 使得y+(-y)=0=(-y)+y(负向量的存在性)。
使得y+(-y)=0=(-y)+y(负向量的存在性)。标量乘法的公理
1.a(by) = (ab)y 对所有向量y和所有标量a,b成立,称为标量乘法的结合律;
2.a(x + y) =ax+ay对所有向量a, y ∈V和标量a成立,称为标量乘法的分配律;
3. (a+ b)y = ay+ by对所有向量g和所有标量α,b成立(标量乘法的分配律);
4.1g = y对所有y ∈V成立,称为标量乘法的单位律。
定义2 令V和w是两个向量空间,若W是V中一个非空的子集合,则称子集合W是V的个子空间。
定理1 如果V是一个向量空间,则
(1)零向量0是唯一的。
(2)对每一个向量y,加法的逆运算-y是唯一的。
(3)对每一个向量y,恒有0y = 0。
(4)对每一个标量a,恒有a0= 0。
(5)若ay =0,则a=0或者y = 0。
(6)(-1)y = -y。
定理2 P”的子集合W是R”的子空间,当且仅当以下三个条件满足:
(1)每当向量x, y属于W,则a +y 也属于W,即满足加法的闭合性:
(2)每当向量x属于W,且 a为标量时,则ax属于W,即满足与标量乘积的闭合性。
(3)零向量0是W的元素。
-
相关阅读:
性能问题从发现到优化一般思路
elasticsearch,为什么prefix性能消耗很大
kafka的安装和基本操作
Redis系列之常见数据类型应用场景
23年基因蓝皮书略读
[Ansible专栏]Ansible安装和基本使用
【C语言】字符串、字符数组
染色法判定二分图的算法
CSDN21天学习挑战赛 - 第二篇打卡文章
spring authorization server授权中心
- 原文地址:https://blog.csdn.net/Xiao__fly/article/details/125543014