62. 不同路径

https://leetcode.cn/problems/unique-paths/

思路：对于每个位置(i,j), 它可以从两个位置过来，一个是上面，一个是左边，所以(i,j)位置可达的路径为 $dp[i][j]=dp[i-1][j]+dp[i][j-1]$, 边界条件包括第一行和第一列，第一行和第一列只有一条路径可以达到，初始化为1

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m][n];
        for(int i=0;i<m;i++){//第一列只有1种路径达到
            dp[i][0]=1;
        }
        for(int j=0;j<n;j++){//第一行只有1种路径达到
            dp[0][j]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}
//O(mn)
//O(mn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

63. 不同路径 II

https://leetcode.cn/problems/unique-paths-ii/

思路：同不同路径I这道题，这里的递推公式只有当当前位置没有障碍物时才满足条件，另外在初始化边界条件时，遇到障碍物就停止初始化，因为后面都是不可达到的

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length,n=obstacleGrid[0].length;
        int[][] dp=new int[m][n];
        for(int i=0;i<m&&obstacleGrid[i][0]==0;i++){//初始化第一列 遇到障碍物则从障碍物开始往后都不可达
            dp[i][0]=1;
        }
        for(int j=0;j<n&&obstacleGrid[0][j]==0;j++){//初始化第一行 遇到障碍物则从障碍物开始往后都不可达
            dp[0][j]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]==0){//位置(i,j)没有障碍物
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
}
//O(mn)
//O(mn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

64. 最小路径和

https://leetcode.cn/problems/minimum-path-sum/

思路：和不同路径这两道题目类似，首先初始化第一行和第一列，作为边界条件处理，然后对于其他的位置(i,j), 状态转移方程为: $dp[i][j]=min(dp[i-1][j],dp[i][j-1]+grid[i][j]$, 最后返回dp[m-1][n-1]

class Solution {
    public int minPathSum(int[][] grid) {
        int m=grid.length,n=grid[0].length;
        int[][] dp=new int[m][n];
        dp[0][0]=grid[0][0];
        for(int i=1;i<m;i++){//初始化第一列
            dp[i][0]=dp[i-1][0]+grid[i][0];
        }
        for(int j=1;j<n;j++){//初始化第一行
            dp[0][j]=dp[0][j-1]+grid[0][j];
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                //当前位置右上面和左边格子中的较短路径移动而来
                dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
}
//O(mn)
//O(mn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

5. 最长回文子串

https://leetcode.cn/problems/longest-palindromic-substring/

思路：对于一个子串s[i:j] ,当s[i:j] 是回文串时，有s[i+1:j-1]是回文串并且s[i]=s[j]

d p [ i ] [ j ] = { t r u e , if i=j s [ i ] = s [ j ] & & d p [ i + 1 ] [ j − 1 ] , dp[i][j]=

dp[i][j]={true,s[i]=s[j]&&dp[i+1][j−1],​if i=j

class Solution {
    public String longestPalindrome(String s) {
        int n=s.length();
        if(n<2){
            return s;
        }
        int start=0;
        int maxLen=1;
        boolean[][] dp=new boolean[n][n];
        for(int i=0;i<n;i++){
            dp[i][i]=true;//单个字符是回文串
        }
        for(int len=2;len<=n;len++){
            for(int i=0;i<n;i++){//i是开始位置
                int j=i+len-1;//j是结束位置
                if(j>=n){//越界
                    break;
                }
                if(s.charAt(i)!=s.charAt(j)){//s[i]!=s[j]
                    dp[i][j]=false;
                }else{//s[i]=s[j]
                    if(j-i<3){//长度为2&s[i]=s[j] 直接是回文串
                        dp[i][j]=true;
                    }else{
                        dp[i][j]=dp[i+1][j-1];
                    }
                }
                if(dp[i][j]&&j-i+1>maxLen){//s[i:j]是回文串并且串更长
                    maxLen=j-i+1;
                    start=i;
                }
            }
           
        }
        return s.substring(start,start+maxLen);
    }
    
}
//O(n^2)
//O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

剑指 Offer II 091. 粉刷房子

https://leetcode.cn/problems/JEj789/

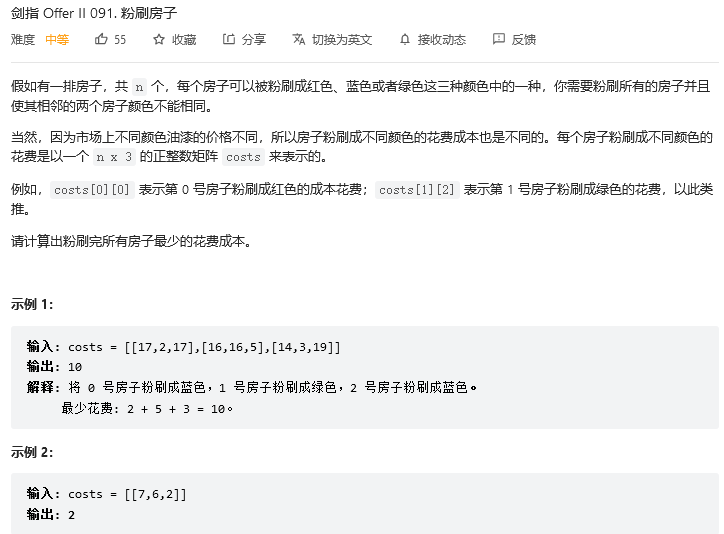
思路：动态规划，dp[i][j]表示粉刷了房子0号到i号并且i号房子颜色是j(0: 红色 1：蓝色 2：绿色)
则状态转移方程为：

$$\begin{gathered} dp[i][0]=min(dp[i-1][1],dp[i-1][2])+cost[i][0] \\ dp[i][1]=min(dp[i-1][0],dp[i-1][2])+cost[i][1] \\ dp[i][2]=min(dp[i-1][0],dp[i-1][1])+cost[i][2] \end{gathered}$$

当染0号房子时，dp[0][0]=cost[0][0]，dp[0][1]=cost[0][1]，dp[0][2]=cost[0][2], 为了节省空间开销，可以直接使用已有的costs数组作为dp数组

class Solution {
    public int minCost(int[][] costs) {
        int n=costs.length;
        for(int i=1;i<n;i++){
            costs[i][0]=Math.min(costs[i-1][1],costs[i-1][2])+costs[i][0];
            costs[i][1]=Math.min(costs[i-1][0],costs[i-1][2])+costs[i][1];
            costs[i][2]=Math.min(costs[i-1][0],costs[i-1][1])+costs[i][2];
        }
        return Math.min(costs[n-1][0],Math.min(costs[n-1][1],costs[n-1][2]));
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13

53. 最大子数组和

https://leetcode.cn/problems/maximum-subarray/

思路：dp[i]表示以数组元素nums[i]结尾的最大连续子数组和
$dp[i]=max(dp[i-1]+nums[i],nums[i])$, 如果加上dp[i-1]的连续和更大则加上，否则以nums[i]结尾的最大连续和就是nums[i], 然后找出所有的dp[i]中最大的，即位整体的最大连续子数组和

class Solution {
    public int maxSubArray(int[] nums) {
        int n=nums.length;
        int[]dp=new int[n];
        int maxSum=nums[0];
        dp[0]=nums[0];
        for(int i=1;i<n;i++){
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            maxSum=Math.max(maxSum,dp[i]);

        }
        return maxSum;
    }
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

121. 买卖股票的最佳时机

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/

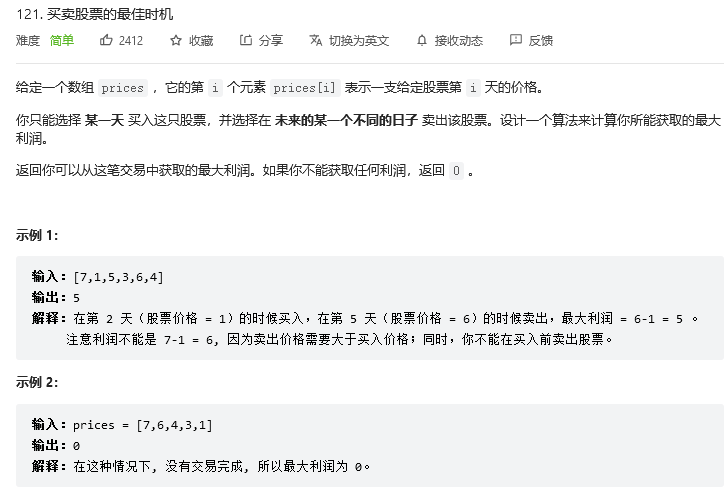
思路：状态转移方程为$dp[i]=max(dp[i-1],prices[i]-minPrice)$, dp[i]表示[0-i]天内可以取得的最大利润，最大利润在前i-1天的最大利润和第i天卖出获得的利润中取最大值

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int minPrice=prices[0];
        int[] dp=new int[prices.length];
        dp[0]=0;//第0天没有利润
        for(int i=1;i<n;i++){
            minPrice=Math.min(minPrice,prices[i]);//更新[0:i]区间内的最小价格
            dp[i]=Math.max(dp[i-1],prices[i]-minPrice);//第i天卖出  最小价格那天买入（假设第j天价格最低 j属于[0:i-1]）
               //更新最大利润
            
        }
        return dp[n-1];
    }
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

由于每次只会用到上一状态的值，可以将dp数组简化为一个变量maxProfit, 减小空间开销

class Solution {
    public int maxProfit(int[] prices) {
        int minPrice=prices[0];
        int maxProfit=0;
        for(int i=1;i<prices.length;i++){
            minPrice=Math.min(minPrice,prices[i]);//更新[0:i]区间内的最小价格
            maxProfit=Math.max(maxProfit,prices[i]-minPrice);//第i天卖出  最小价格那天买入（假设第j天价格最低 j属于[0:i-1]）
               ;//更新最大利润
            
        }
        return maxProfit;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

122. 买卖股票的最佳时机 II

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/

思路：在某一天手里可能没有股票，手里可能有一支股票，记作dp[i][0]为在第i天手里没有股票时可以获得的最大利润，dp[i][1]为在第i天手里有1支股票时可以获得的最大利润

dp[i][0]可以从两个状态转移过来：

1. 第i-1天手里没有股票
2. 第i-1天手里有股票，但是第i天卖了

故dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]

dp[i][1]可以从两个状态转移过来：

1. 第i-1天手里有股票
2. 第i-1天手里没有股票，但是第i天买了一支股票

故dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int[][] dp=new int[n][2];
        dp[0][0]=0;//第0天手里没有股票的利润为0
        dp[0][1]=-prices[0];//第0天买入 因此利润为负值
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
        }
        return Math.max(dp[n-1][0],dp[n-1][1]);
    }
}
//O(n)
//O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

上面的状态转移方程中，每一天的状态只与前一天的状态有关，而与更早的状态都无关, 因此可以将dp二维数组用两个变量表示，减小空间开销

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int dp0=0;//第0天手里没有股票的利润为0
        int dp1=-prices[0];//第0天买入 因此利润为负值
        for(int i=1;i<n;i++){
            dp0=Math.max(dp0,dp1+prices[i]);
            dp1=Math.max(dp1,dp0-prices[i]);
        }
        return Math.max(dp0,dp1);
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

123. 买卖股票的最佳时机 III

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/

思路：在任意一天结束后，我们会处于以下5种状态中的一种

1. 未进行过任何操作
2. 只进行过一次买操作
3. 进行过一次买操作和一次卖操作，即完成一次交易
4. 完成了一次交易后又进行了一次买操作
5. 完成了两次交易

状态1没有进行任何操作，因此利润为0，此种状态不考虑，对其他四种状状态最大利润分别记为buy1 sell1 buy2 sell2

{ b u y 1 = m a x ( b u y 1 , − p r i c e s [ i ] ) s e l l 1 = m a x ( s e l l 1 , b u y 1 + p r i c e s [ i ] b u y 2 = m a x ( b u y 2 , s e l l 1 − p r i c e s [ i ] ) s e l l 2 = m a x ( s e l l 2 , b u y 2 + p r i c e s [ i ] )

⎩⎪⎪⎪⎨⎪⎪⎪⎧​buy1=max(buy1,−prices[i])sell1=max(sell1,buy1+prices[i]buy2=max(buy2,sell1−prices[i])sell2=max(sell2,buy2+prices[i])​

边界条件：对于第0天，buy1=-prices[i], sell1表示当天买入一次卖出一次，因此sell1=0, buy2表示当天完成一次交易后又买入一次，因此buy2=-prices[i], sell2=0

返回值：最大利润肯定是取决于卖出后的利润，假设完成一次交易的利润最大，那么可以在当天再进行一次交易，这样sell1的状态就能够转移到sell2的状态，因此最终返回sell2

class Solution {
    public int maxProfit(int[] prices) {
        int buy1=-prices[0],sell1=0;
        int buy2=-prices[0],sell2=0;
        for(int i=1;i<prices.length;i++){
            buy1=Math.max(buy1,-prices[i]);//(未进行操作,当天买入)
            sell1=Math.max(sell1,buy1+prices[i]);//(未进行操作,上一次买入后卖出)
            buy2=Math.max(buy2,sell1-prices[i]);//(未进行操作,上一次卖出后买入)
            sell2=Math.max(sell2,buy2+prices[i]);//(未进行操作,上一次买入后卖出)
        }
        return sell2;
    }
}
//O(n)
//O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

188. 买卖股票的最佳时机 IV

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/

思路：第一步考虑n/2和k的大小关系，如果k>=n/2, 相当于不受限制次数的交易，此时转化为122. 买卖股票的最佳时机 II， 对该问题我们可以使用贪心算法来解决； 当k<n/2时，使用动态规划

定义buy[i][j] 表示第i天进行第j次交易（第j次买入股票）时的最大利润
定义sell[i][j] 表示第i天进行第j次交易（第j次卖出股票）时的最大利润

$buy[i][j]=max(buy[i-1][j],sell[i-1][j-1]-prices[i])$: max（第i天不进行交易，在第i-1天第j-1次交易的基础上买入一支股票）

$sell[i][j]=max(sell[i-1][j],buy[i][j]+prices[i])$: max（第i天不进行交易，在第i天第j次交易的基础上买入一支股票）

class Solution {
    public int maxProfit(int k, int[] prices) {
        if (prices.length == 0) {
            return 0;
        }

        int n = prices.length;
        if(k>=n/2){
            return greedy(prices);
        }
        int[][] buy = new int[n][k + 1];
        int[][] sell = new int[n][k + 1];

        buy[0][0] = 0;
        sell[0][0] = 0;
        for (int i = 1; i <= k; ++i) {
            buy[0][i] = -prices[0];
            sell[0][i]=0;
        }

        for (int i = 1; i < n; ++i) {
            for (int j = 1; j <= k; ++j) {
                buy[i][j] = Math.max(buy[i - 1][j], sell[i - 1][j-1] - prices[i]);
                sell[i][j] = Math.max(sell[i - 1][j], buy[i][j]+prices[i]); 
                //第i天进行了第j次交易的买入->第i天进行了第j次交易的卖出
                // buy[i][j]+prices[i]-->sell[i][j]  
                //第i-1天进行了第j次交易的买入->第i天进行了第j次交易的卖出
                //buy[i - 1][j]+prices[i]-->sell[i][j]
                //由于buy[i][j]>=buy[i - 1][j]  因此这里只需要写buy[i][j]+prices[i]
                
            }
        }

        return Arrays.stream(sell[n - 1]).max().getAsInt();
    }
    public int greedy(int[] prices){
        int ans=0;
        for(int i=1;i<prices.length;i++){
            if(prices[i]-prices[i-1]>0){
                ans+=prices[i]-prices[i-1];
            }
        }
        return ans;
    }
}
//O(nk)  走greedy的时间是n  不走的时间是nk
//O(nk)  走greedy的时间是1  不走的时间是nk



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50