-
【MDP】①二次规划问题MATLAB求解器quadprog
一、概述
二次规划是指约束为线性的二次优化问题。在Matlab中,quadprog是具有线性约束的二次目标函数求解器。
(一)二次规划标准形式
min x 1 2 x T H x + f T x \mathop {\min }\limits_x \frac{1}{2}{{\bf{x}}^{\bf{T}}}{\bf{Hx}} + {{\bf{f}}^{\bf{T}}}{\bf{x}} xmin21xTHx+fTx
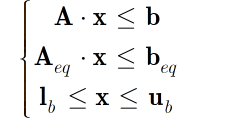
(二)输入参数
符号 参数含义 H 二次目标矩阵 f 线性目标向量 A 线性不等式矩阵 b 线性不等式向量 Aeq 线性等式约束矩阵 beq 线性等式约束向量 lb 下界 ub 上界 (三)输出参数
符号 参数含义 x 解,以实数向量形式返回 wsout 解的热启动对象 fval 再解处的目标函数值 exitflag quadprog停止的原因 output 有关优化过程的信息,以结构体形式返回 lambda 解处的拉格朗日乘数 二、MATLAB基础语法
x = quadprog(H,f) x = quadprog(H,f,A,b) x = quadprog(H,f,A,b,Aeq,beq) x = quadprog(H,f,A,b,Aeq,beq,lb,ub) x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0) x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) x = quadprog(problem) [x,fval] = quadprog(___) [x,fval,exitflag,output] = quadprog(___) [x,fval,exitflag,output,lambda] = quadprog(___) [wsout,fval,exitflag,output,lambda] = quadprog(H,f,A,b,Aeq,beq,lb,ub,ws)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
三、MATLAB典型求解样例
(一)具有线性不等式约束的二次规划

H = [1 -1; -1 2]; f = [-2; -6]; A = [1 1; -1 2; 2 1]; b = [2; 2; 3]; [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b);- 1
- 2
- 3
- 4
- 5
x =
0.6667
1.3333 fval = -8.2222 exitflag =
1(二)具有线性等式约束的二次规划

H = [1 -1; -1 2]; f = [-2; -6]; Aeq = [1 1]; beq = 0; [x,fval,exitflag,output,lambda] = ... quadprog(H,f,[],[],Aeq,beq)- 1
- 2
- 3
- 4
- 5
- 6
x = -0.8000
0.8000 fval = -1.6000 exitflag =
1(三)具有线性约束和边界的二次规划
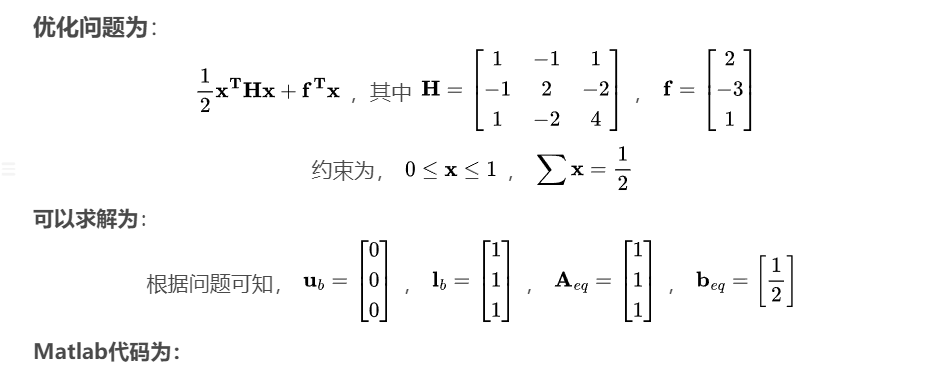
H = [1,-1,1 -1,2,-2 1,-2,4]; f = [2;-3;1]; lb = zeros(3,1); ub = ones(size(lb)); Aeq = ones(1,3); beq = 1/2; x = quadprog(H,f,[],[],Aeq,beq,lb,ub);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
-
相关阅读:
工作遇到的问题以及解决处理方法-主要是基于vue的antd
mysql实际调优
Casein-PEG-Rhodamine B 络蛋白-聚乙二醇-罗丹明B Casein-RB
【Linux】高频指令及简单的vim使用(0基础带你快速入门)
Eureka Server 实现在线扩容
sheetJs+xlsx-style——前端实现导出excel表格——设置单元格背景色,居中,自动换行,宽度,百分数展示等
ArcGIS实战教程
【BW16 应用篇】安信可BW16模组/开发板AT指令实现HTTP通讯
Tomcat
补充:js 制作qq、微信 的表情 缺少的微信表情图片
- 原文地址:https://blog.csdn.net/zeye5731/article/details/125530324