一. 决策树概述

1.1 什么是决策树

决策树输入: 测试集
决策树输出: 分类规则(决策树)

1.2 决策树算法概述

决策树的几种常见实例

1. ID3决策树
2. C4.5决策树
3. CART分类（回归）树

变量信息增益最大，才是最重要的变量，放在最上面
变量的值有很多，但是在训练集里面是有限的，所以可以标记出来

二. 决策树的构造

2.1 决策树的构造：分而治之（divide and conquer）

决策树是典型的局部与整体存在相似性的模型，即任意一条路径中，任意一个内部节点都形成以它为根节点的“子决策树”。对于这样形态的模型，高效、可行的构造方法就是分而治之。步骤如下：
输入：数据集$D=(x_1,y_1),(x_2,y_2),..,(x_m,y_m)$及其特征空间$A=a_1,a_2,\dots ,a_d$
函数TreeGenerate(D，A)

1. 生成节点Node
2. 如果数据集D全部属于某类别C，则将1中的节点Node划分为属性C，返回
3. 如果A为空集，或者D在A上的取值完全一致，则1中的节点Node标记为叶节点，所属类别为D中占大多数的类别，返回
4. 选择最优分裂节点a，
   For each value $a^V$ in a:
   从节点Node生成一个分支，令数据集𝐷_𝑉是D在a中取值为$a^V$的子集
   if 𝐷_𝑉是空集，则该分支作为叶节点，所属类别是D中大多数的类别，返回；else 生成分支 TreeGenerate(𝐷_𝑉, A{a})
   End for

这是一个典型的递归过程，返回条件是：

1. 当前节点包含的样本属于同一类别
2. 当前属性为空
3. 所有属性取值相同
4. 当前节点包含的样本集为空

叶节点的输出：
叶子节点输出占比最大的类别，也就是输出概率最大的类别。如果改造成输出每个类别对应的概率，则可以用在随机森林中输出概率的计算。

两个问题：如何选择最优属性？如何分裂节点？
最优属性的选择

1. 信息增益和信息增益率
2. 基尼指数
   分裂节点
3. 离散型，取值种类少
4. 离散型，取值种类多
5. 连续型

2.2 信息增益（Information Gain）

衡量类别纯度的信息熵：
假设样本D中第k类样本占比为$p_K$,则D的信息熵定义为
$$Entropy(D)=-\sum _k{p}_{k}lo{g}_2{p}_k$$
Entropy越小，纯度越高

信息熵：entropy 它表示了信息的不确定度 换句话说就是数据的混沌程度，以贷款举例，2人逾期，2人未逾期那么混沌程度最高，不确定性最高，信息熵就最大。纯度就最低。

信息增益：
若D被属性a划分成$D={\bigcup }_v{D}_v,D_v\cap D_w=\varnothing$，定义信息增益为：
$$Gain(D,a)=Entropy(D)-\sum _v\frac{|D_v|}{|D|}Entropy(D_v)$$

现在我们有一份数据集D（例如贷款信息登记表）和特征A（例如年龄），则A的信息增益就是D本身的熵与特征A给定条件下D的条件熵之差，即：
$$g(D,A)=H(D)-H(D|A)$$
数据集D的熵是一个常量。信息增益越大，表示条件熵 越小，A消除D的不确定性的功劳越大。

所以要优先选择信息增益大的特征，它们具有更强的分类能力。由此生成决策树，称为ID3算法。

信息增益的作用和特点：

1. 衡量从无序到有序的变化程度（常用于ID3决策树）
2. 选择具有最大信息增益的属性进行分裂
3. 不具有泛化能力，对取值较多的属性有偏好
   为了控制属性取值数目的影响，先定义IV：
   $$IV(a)=-\sum _v\frac{|D_v|}{|D|}lo{g}_2\frac{|D_v|}{|D|}$$

2.3 信息增益率

当某个特征具有多种候选值时，信息增益容易偏大，造成误差。引入信息增益率可以校正这一问题。
信息增益率为信息增益与数据集D的熵之比：
$$GainRatio=\frac{Gain(D,a)}{IV(a)}$$

特性：
容易倾向取值较少的属性
可以选择具有最大增益率的属性进行分裂
可以选择大于平均增益率的属性集，再选择增益率最小的属性

2.4 基尼指数

另一种衡量纯度的指标
$$Gini(D)=1-\sum _k{p}_k^2$$
Gini越小，纯度越高
属性a在数据集D中的基尼指数是
$$Gini(D,a)=\sum _v\frac{|D_v|}{|D|}Gini(D_v)$$
选择具有最小基尼指数的属性，即$a_{\ast }=argminGini(D,a)$

2.5 示例

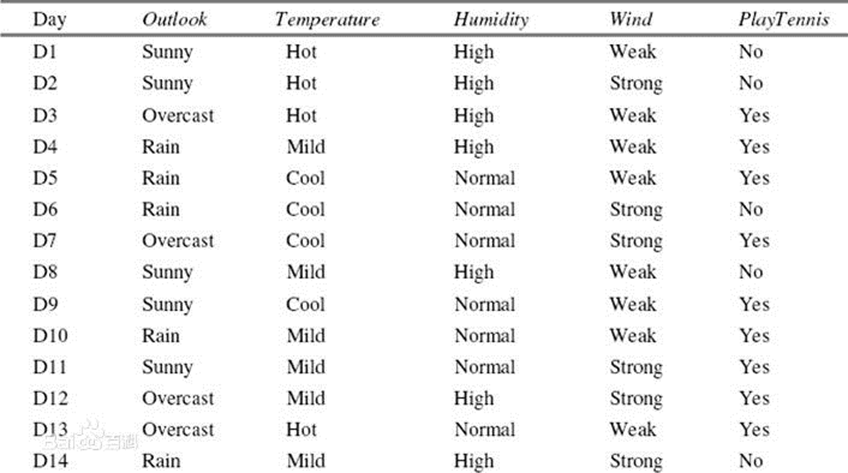
一个简单的例子：用变量outlook，temperature，humidity，wind来对playtennis进行分类。

对于outlook，它的信息增益率的计算方式为：
（1）总体的熵的计算：
P(PlayTennis=Yes) = 9/14, P(PlayTennis=No) = 5/14
Entropy = -9/14*log2(9/14) – 5/14*log2(5/14) =0.9403
（2）将数据集D按照Outlook进行划分，结果为：
D1: Outlook=Sunny有5个样本，其中PlayTennis=Yes有2个样本，PlayTennis=No有3个样本
Entropy1 = -2/5*log2(2/5)-3/5*log2(3/5) =0.9710
D2: Outlook=Overcast有4个样本，其中PlayTennis=Yes有4个样本，PlayTennis=No有0个样本
Entropy2 = -0/4*log2(0/4)-4/4*log2(4/4) =0 (定义0*log2(0)=0)
D3: Outlook=Rain有5个样本，其中PlayTennis=Yes有3个样本，PlayTennis=No有2个样本
Entropy3 = -3/5*log2(3/5)-2/5*log2(2/5) = 0.9710
（3）计算IV： IV=-5/14*log2(5/14)-4/14*log2(4/14)-5/14*log2(5/14)= 1.5774
（4）计算信息增益：Gain = 0.9403-5/14* 0.9710-4/14*0-5/14* 0.9710= 0.2467
（5）计算信息增益率：Gain Ratio= 0.2467/ 1.5774= 0.1564

计算Outlook的Gini：
（1）计算D1，D2和D3的Gini：
Gini1 = 1-(2/5)^2-(3/5)2=0.4800，Gini2 = 1-(4/4)^2-(0/4)2=0
Gini3 = 1-(2/5)^2-(3/5)2=0.4800
（2）计算总体的Gini:
Gini(D)=5/140.4800 + 4/140 + 5/15* 2=0.4800= 0.3086

2.6 连续变量的处理

连续变量通过二分法离散化，然后当成离散变量来处理。

三. 防止拟合：剪枝的艺术

有很大的概率，所有属性都拿来分裂，易造成过拟合

避免过拟合，需要剪枝(pruning)。剪枝的两种方法

1. 预剪枝
   在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶节点
2. 后剪枝
   先从训练集中生成一颗完成的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换成叶节点能提升决策树泛化性能，则将该子树替换成叶节点

**泛化能力：**算法对新鲜样本的适应能力。可以用留出法，即在训练集中再次抽选出一部分不参与决策树构造，而用于评估某一次对某节点划分或者子树合并的测试。

四. 提升分类器准确率的组合方法

4.1 组合方法概述

为什么组合方法能够提高分类准确率

组合算法的优势

4.2 装袋算法

有放回抽样:

装袋算法的优势:

4.3 提升(boosting)算法思想

Adaboost算法:

提升算法的优缺点:

4.4 随机森林

决策树的加强算法: 随机森林

4.4.1 随机森林的基本概念

随机森林属于集成模型的一种。它由若干棵决策树构成，最终的判断结果由每一棵决策树的结果进行简单投票决定。

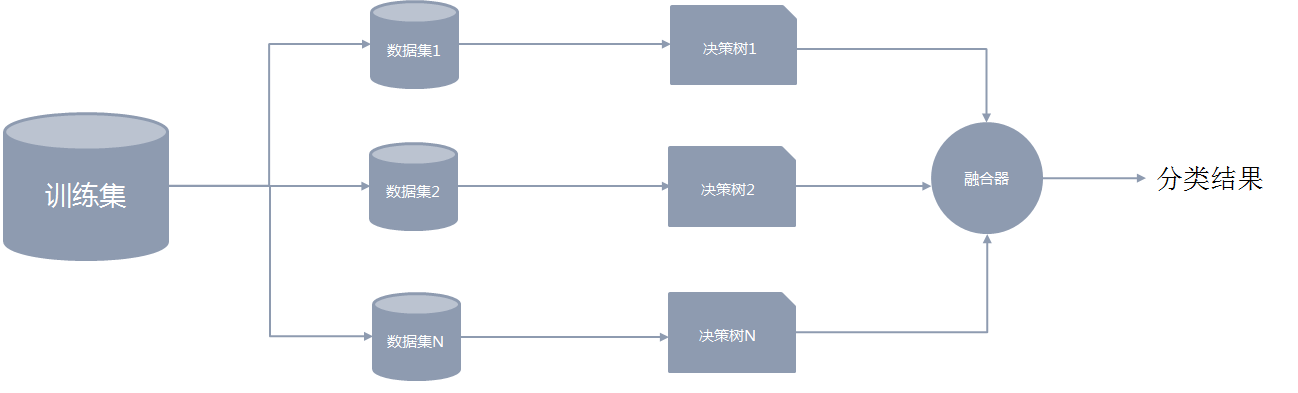
4.4.2 数据集的抽取

在构建随机森林模型的过程中，关键的一步是要从原数据集中多次有放回地抽取一部分样本组成新的训练集，且样本量保持不变。后续每一个决策树模型的构建都是分别基于对应的抽样训练集。
“随机森林”中的“随机”二字主要体现在2方面：

1. 从整体的训练集中抽取数据时，样本是有放回地抽取。
2. 组成新的训练集后，再从属性集中无放回地抽取一部分属性进行决策树模型的开发

这些随机操作能很好地增强模型的泛化能力，有效避免了过拟合的问题。也别其他一些模型所借鉴（例如极大梯度提升树）。
在1中，每次有放回地生成同等样本量的数据集时，大约有1/3的样本没有被选中，留作“袋外数据”
在2中，假设原有m个属性，在第2步中一般选择log_2⁡𝑚个属性进行决策树开发。

4.4.3 决策树结果的融合

得到若干棵决策树后，会对模型的结果进行融合。在随机森林中，融合的方法通常是简单投票法。假设K棵决策树的投票分别是𝑡_1, 𝑡_2,…,𝑡_𝐾, 𝑡_𝑖∈{0,1}，最终的分类结果是

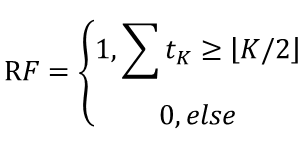
随机森林的输出概率
同时随机森林也支持以概率的形式输出结果：

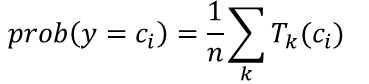
参考:

1. http://www.dataguru.cn/article-4063-1.html
2. https://zhuanlan.zhihu.com/p/76590801