矩阵分析与应用 - 码农知识堂

矩阵分析与应用

函数向量的内积与范数

若和分别是变量t的函数向量，则它们的内积定义为：

$\left \langle x(t),y(t) \right \rangle=\int_{a}^{b}x^{H}(t)y(t)dt$

其中，变量t在[a,b]取值，且a<b。变量t可以是时间变量、频率变量或者空间变量。

两个函数向量的夹角定义为：

$cos\theta =\frac{\left \langle x,y \right \rangle}{\sqrt{\left \langle x,x \right \rangle}\sqrt{\left \langle y,y \right \rangle}}=\frac{\int_{a}^{b}x^{H}(t)y(t)dt}{\left \| x(t) \right \|\left \| y(t) \right \|}$
式中， $\left \| x(t) \right \|$ 是函数向量的范数，定义为：

$\left \| x(t) \right \|=\left (\int_{a}^{b}x^{H}(t)x(t)dt \right )^{1/2}$
显然，若两个函数向量的内积等于零，即

$\int_{-\infty}^{\infty}x^{H}(t)y(t)dt=0$

则 $\theta =\frac{\pi }{2}$ 。此时称两个函数向量正交，并记作 $x(t)\perp y(t)$

随机向量的内积与范数

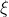若 $x(\xi)$ 和 $y(\xi)$ 分别是样本变量 $\xi$ 的随机向量，则它们的内积定义为：

$\left \langle x(\xi),y(\xi) \right \rangle=E\left \{ x^{H}(\xi)y(\xi) \right \}$

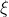其中，样本变量 $\xi$ 可以是时间，圆频率，角频率和空间变量等。

随机向量 $x(\xi)$ 的范数定义为：
$\left \| x(\xi) \right \|^{2}=E\left \{ x^{H}(\xi)x(\xi) \right \}$

与常数向量和函数向量的情况不同，若 $x(\xi)$ 的任意元素与的任意元素正交，则m*1随机向量 $x(\xi)$ 和n*1随机向量 $y(\xi)$ 称为正交。这意味着，两个向量的互相关矩阵为零矩阵 $O_{m \times n}$ ，即

$E\left \{ x(\xi)y^{H}(\xi) \right \}=O_{m \times n}$

并记作 $x(\xi)\perp y(\xi)$

Cauchy-Schwartz不等式：

$|\left \langle x,y \right \rangle|\leqslant \left \| x \right \|\left \| y \right \|$ 仅当 $x=\lambda y$ 或或时等号成立。

平行四边形法则：

$\left \| x+y \right \|^{2}+\left \| x-y \right \|^{2}=2\left \| x \right \|^{2}+2\left \| y \right \|^{2}$

Pythagorean定理：

若 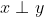$x\perp y$ ，则 $\left \| x+y\right \|^{2}=\left \| x\right \|^{2}+\left \| y\right \|^{2}$

证明：由范数公理知：

$\left \| x+y\right \|^{2}=\left \langle x+y,x+y \right \rangle=\left \langle x,x \right \rangle+\left \langle x,y \right \rangle+\left \langle y,x \right \rangle+\left \langle y,y \right \rangle$

由于x和y正交，所以 $\left \langle x,y \right \rangle=E\left \{ x^{T}y \right \}=0$ 。

又由内积公理 $\left \langle y,x \right \rangle=\left \langle x,y \right \rangle=0$ 知。将这一结果代入上式可得：
$\left \| x+y\right \|^{2}=\left \langle x,x \right \rangle+\left \langle y,y \right \rangle=\left \| x \right \|^{2}+\left \|y \right \|^{2}$

即命题得证。
相关阅读:
OmniShade - Mobile Optimized Shader
位图(bitmap)原理以及实现
 Docker镜像解析获取Dockerfile文件
 crmeb知识付费2.1免授权版本，包含PC端，可包更新
 如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。
基础图论算法--最小生成树——prim、Kruskal算法
 pytorch Nvidia 数据预处理加速
 C++-类与对象(上)
java基础05
Spring 源码（2）Spring IOC 容器前戏准备工作
原文地址：https://blog.csdn.net/weixin_46007132/article/details/125451805