一.用队列实现栈

力扣

在做这道题前，我们需要有 栈 的先驱知识，可以参考本人的这篇博客

(41条消息) 【数据结构】栈_Living_Amethyst的博客-CSDN博客 

 

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

分析：

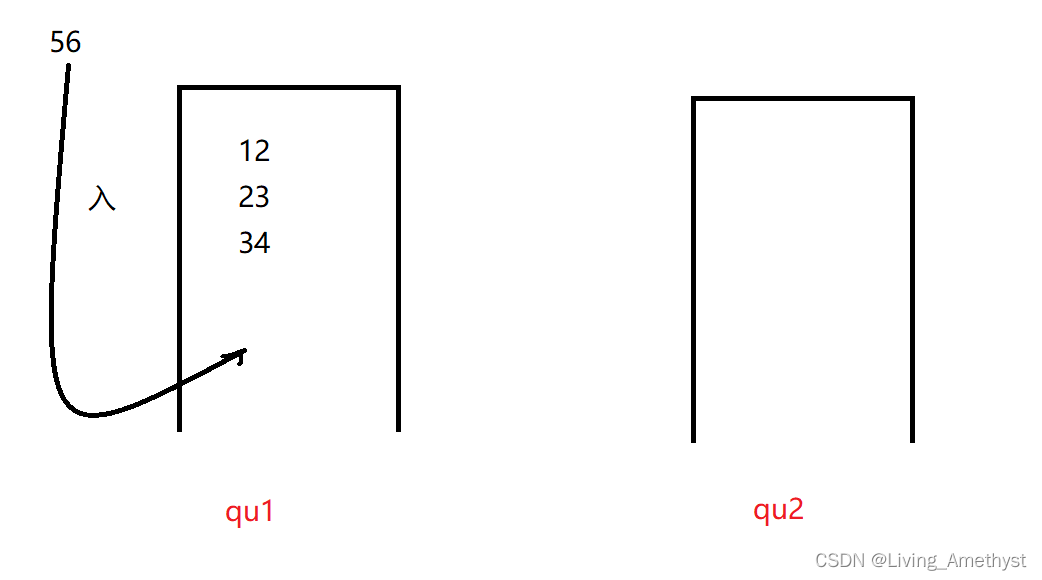
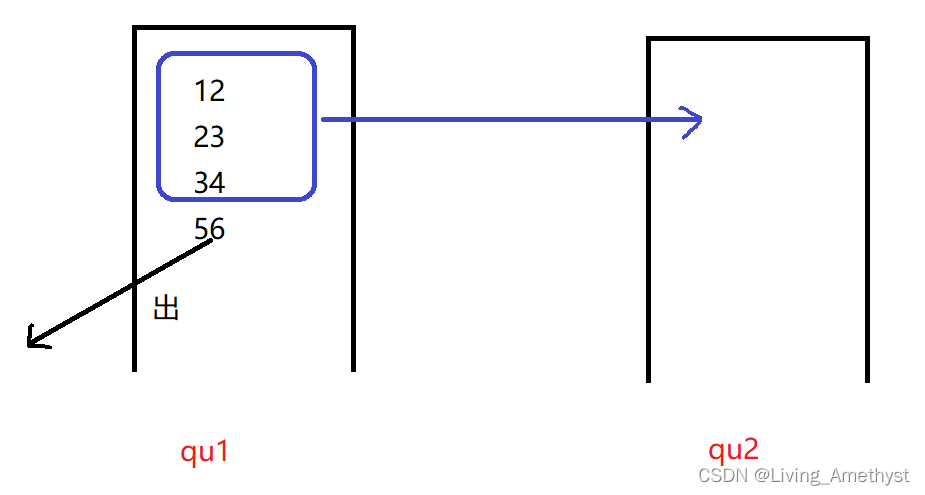
由于队列的特点是“先进先出”，而栈的特点是“后入先出”，所以用队列实现栈 仅用一个队列是不能实现的，需要两个队列

我们的思路是：入的时候都入到不为空的队列里，出的时候就把不为空的队列里的除了要出的元素之外的其他(size-1)个元素都移到为空的队列里

 

 

 

import java.util.LinkedList;
import java.util.Queue;
 
class MyStack {
    private Queue<Integer> qu1;
    private Queue<Integer> qu2;
 
    public MyStack() {
        qu1 = new LinkedList<>();
        qu2 = new LinkedList<>();
    }
 
    /**
     * 入到不为空的队列中
     * 如果都为空，就入到qu1中
     * @param x
     */
    public void push(int x) {
        if(!qu1.isEmpty()){
            qu1.offer(x);
        }else if(qu2.isEmpty()){
            qu2.offer(x);
        }else{
            qu1.offer(x);
        }
    }
    
    public int pop() {
        //1.判断当前“栈”是否为空
        if(empty()){
            return  -1;
        }
        if(!qu1.isEmpty()){
            //从不为空的队列里出 size-1 个元素
            int size = qu1.size();
            for (int i = 0; i < size-1; i++) {
                /*
                int tmp = qu1.poll();
                qu2.offer(tmp);
                 */
                qu2.offer(qu1.poll());
            }
            return qu1.poll();
        }else{
            //从不为空的队列里出 size-1 个元素
            int size = qu2.size();
            for (int i = 0; i < size-1; i++) {
                /*
                int tmp = qu1.poll();
                qu2.offer(tmp);
                 */
                qu1.offer(qu2.poll());
            }
            return qu2.poll();
        }
    }
    
    public int top() {
        //1.判断当前“栈”是否为空
        if(empty()){
            return  -1;
        }
        if(!qu1.isEmpty()){
            //从不为空的队列里出 size个元素
            int size = qu1.size();
            int tmp = -1;
            for (int i = 0; i < size; i++) {
                tmp = qu1.poll();
                qu2.offer(tmp);
            }
            return tmp;
        }else{
            //从不为空的队列里出 size个元素
            int size = qu2.size();
            int tmp = -1;
            for (int i = 0; i < size; i++) {
                tmp = qu2.poll();
                qu1.offer(tmp);
            }
            return tmp;
        }
 
    }
    
    public boolean empty() {
        if (qu1.isEmpty() && qu2.isEmpty()) {
            return true;
        }
        return false;
 
    }
}

 

二.用栈实现队列

力扣 

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

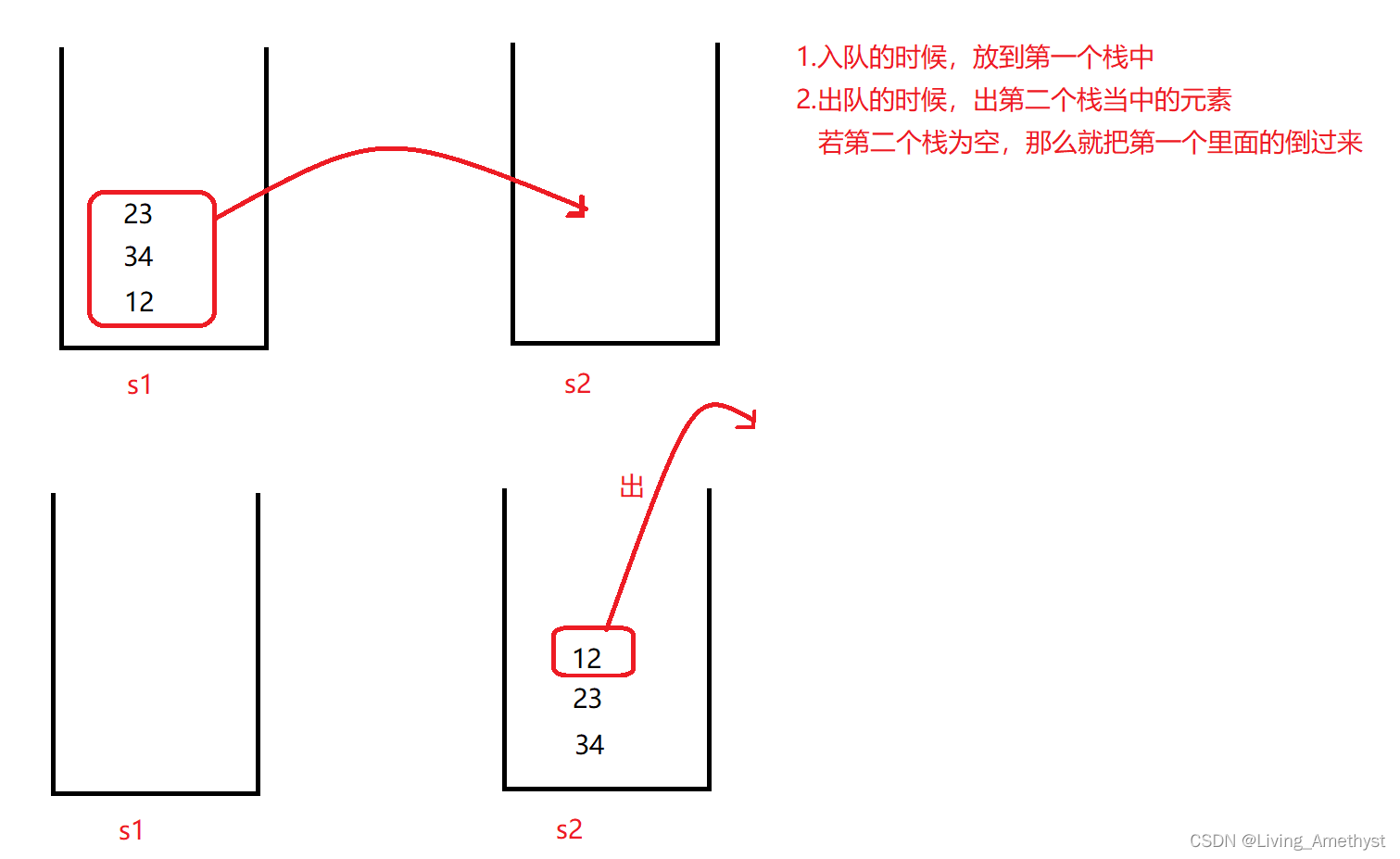
分析：和上一题类似，若要用栈实现队列，我们需要两个栈

 

import java.util.Stack;
class MyQueue {
    private Stack<Integer> s1;
    private Stack<Integer> s2;
 
    public MyQueue() {
        s1 = new Stack<>();
        s2 = new Stack<>();
    }
    
    public void push(int x) {
        //入队的逻辑是把元素统一放到第一个栈中
        s1.push(x);
    }
    //如果第二个栈不为空，则出栈顶元素，否则把第一个栈的元素全部导入第二个栈
    public int pop() {
        if(empty()){
            return -1;//两个栈都是空
        }
        if (s2.empty()){
            //把第一个栈的元素全部导入第二个栈
            while(!s1.empty()){
                s2.push(s1.pop());
            }
        }
        //s2一定是不为空的
        return s2.pop();
    }
    
    public int peek() {
        if(empty()){
            return -1;//两个栈都是空
        }
        if (s2.empty()){
            //把第一个栈的元素全部导入第二个栈
            while(!s1.empty()){
                s2.push(s1.pop());
            }
        }
        //s2一定是不为空的
        return s2.peek();
    }
    
    public boolean empty() {
        return s1.empty() && s2.empty();
    }
}

 

 

三.实现一个最小栈

力扣 

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

分析：

• 定义两个栈，s1 和 minStack
• 入栈时，s1这个栈是一定会放元素的，
• 而对于minStack这个栈，如果minStack为空，则把元素放入minStack
• 若不为空就把放入s1的元素与minStack的元素比较
• 若大于minStack栈中元素，就不放入minStack栈，若小于minStack栈中元素就放入。
• 出栈时，s1一定要出栈，同时要与minStack栈中元素比较，如果一样，那么minStack中的元素也要出栈

import java.util.Stack;
class MinStack {
    private Stack<Integer> s1;
    private Stack<Integer> minStack;
    public MinStack() {
        s1 = new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int val) {
        s1.push(val);//s1这个栈是一定会放元素的
        if(minStack.empty()){
            minStack.push(val);
        }else{
            int x = minStack.peek();
            if(val <= x){  //这里必须加等号
                minStack.push(val);
            }
        }
    }
    public void pop() {
        int x = s1.pop();
        int x2 = minStack.peek();
        if(x == x2){
            minStack.pop();
        }
    }
    
    //获取当前栈顶元素不删除
    public int top() {
        return s1.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}