【文献阅读】Adaptive Arrays

自适应波束形成技术原理

王一同.自适应天线波束形成抗干扰算法研究[D].哈尔滨工程大学,2023.DOI:10.27060/d.cnki.ghbcu.2023.001389.

自适应波束形成技术是一个对接收信号滤波的过程。从空间入射来的信号源被阵 列天线采样接收，根据阵列信号处理中一定的优化处理准则，可以计算求得各阵元加 权值构成的矢量，通过利用加权矢量对阵列天线各个阵元进行加权控制，最后得到高 增益滤波的期望信号。自适应波束形成技术能够将最大波束增益指向对准期望信号的入射方向，同时在干扰的入射方向角度形成具有输出抑制效果的零陷，从而以最小程 度的损失将期望信号从接收信号中过滤出来。该技术实现过程的原理如图 2.5 所示。 如图 2.5 所示， $N$个自适应阵列天线接收来自方向为$\theta$的来波信号，每个阵元都对 应一个接收通道，并且各个通道都被赋予了加权值，最后对各个加权输出数据求和， 得到系统滤波输出的信号表达式：


根据信号功率计算公式，阵列天线接收信号经过自适应波束形成技术滤波之后的 信号输出功率为：


个人理解
自适应天线的工作如下图所示，将天线波束增益最大的部分对准期望信号，将波束零点对准干扰。自适应天线的核心是其信号处理算法。其抗干扰的原理是依靠信号的零陷。

符号表

由于论文内符号繁杂，这里写了一个符号表

Abstract

文章提出了提出了一种自适应优化阵列天线信噪比的方法。给出了自适应阵与旁瓣对消的关系，并讨论了一种实时自适应实现方法。

Introduction

阵列的方向图可以通过在整个阵列上应用线性相位加权来操纵，并且可以通过对阵列元件的输出进行幅度和相位加权来成形。大多数阵列都是用固定权重来构建的，其设计目的是产生一种在分辨率、增益和低旁瓣之间折衷的方向图。特别吸引人的一点是，根据环境自适应变化权重的方案。在这份报告中，我们展示了如何自适应技术可以应用到天线阵列，以减少其对任何类型的干扰或干扰的敏感性。我们开始的推导“control law”的阵列权重，将最大化阵列输出的SNR中。
SNR优化
众所周知，当来自单元通道的噪声贡献具有相等功率且不相关时，均匀加权阵列给出最大SNR。当接收机噪声和均匀分布的天空噪声是主要噪声贡献时，这些条件近似有效。但是，当存在来自其他带内发射机的定向干扰时。在这个文章中，我们要考虑天线权重，来最大化噪声环境下的SNR。问题就被转化成了找到K通道的optimum coherent combiner。所有的信号都由它们的复包络表示。
K个通道中的每一个通道都包含噪声分量，其复包络由$n_k$表示，第k个通道中的包络功率由${\mu }_{kk}$表示，并且$n_k$和$n_l$的协方差由下式表示：

*代表了共轭。还有另一个公式：

当K个通道表示阵列天线的元件的输出时，协方差项${\mu }_{kl}$由接收机噪声和天线“看到”的所有噪声源的空间分布决定。我们假定这一协方差是已知的。当所需信号出现时，假设它与已知的复数$s_k$成比例出现在K个通道中。信号在信道$k$中用$\alpha s_k$表示。其中$\alpha$定义信号的幅度和时间变化。在具有等间距元件的线性阵列天线中，$s_k$由所需信号的方向确定。
$\theta$是机械视轴，$s_k$表示如下：

$d$是物件的间隔，$\lambda$是波长。问题在于选择权重${\omega }_k$，来让combiner的输出SNR最大化。优化权重由下面这一等式来决定。

$M$是噪声输出的协方差矩阵。$M=[{\mu }_{kl}]$。

以上两个是列向量，为了得到

我们开始写combiner的信号和噪声输出的表达式。
信号的输出是：

这可以方便地用矩阵表示法表示为：

小t、下角标意味着转置。同样，噪声的输出也能被表示为：

此处的N是

预期输出噪声功率为：

算子$E$只会影响噪声项，所以式子可以做如下变形：

$M$在这里是

$M$是噪声分量的协方差矩阵。如果噪声分量是不相关的，则矩阵$M$将是对角矩阵。然而，总的来说，$M$的任何位置都可以有非零元素。当${\mu }_{kl}={\mu }_{lk}^{\ast }$，矩阵$M$就变成了Hermitian矩阵（矩阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等）。它也是正定的，因为输出噪声功率$P_n$在$W\ne 0$时大于零。
由于M是正定厄米特矩阵，它可以通过非奇异坐标变换“对角化”。这意味着存在一种变换，它将问题转化为所有通道具有相等功率且不相关的噪声分量的问题。
假设变换矩阵为A，如下图所示：

在那里所示的变换之后，信号和噪声分量分别变为：
信号的：

噪声的：

上标符号(^)被用来表示变换后的量被怎么变换？矩阵A跟着combiner如下图所示

通过适当地关联在每种情况下使用的权重，可以使其等同于图2-1的combiner。

如果变换矩阵A的输出与权重$\widehat{W_k}$组合，则输出信号将是

同样的，输出噪声会变成

我们注意到在转换后合并通道矩阵$A$和权重向量$\hat{W}$等价于权重向量$A_t\hat{W}$没有变换矩阵。因此，对于同等的产出，我们有

以图2-2中的量表示的输出噪声功率为

由于变换矩阵A去除相关噪声分量并使它们的功率相等，A的噪声分量的协方差矩阵就是K阶恒等矩阵。

通过以上的等式，我们得到了：

如果图2-2和图2-1是的配置是相等的，，我们可以得到

因此

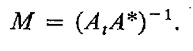
等式(2-29)表示变换矩阵A对角化矩阵M的事实。
图2-2中噪声分量$\widehat{n_k}$功率相等且不相关的加权向量$\hat{W}$的最佳选择为

$\mu$在这里是任意常量。为了展示上面这一式子是优化过的，应用柯西施瓦茨不等式来证明：


上面计算的是W矩阵模的平方。

将W等量代换成$P_n$后，得到上述不等式。这为SNR设置了一个上限。
当把$\hat{W}$用另一个等式替换的话，会得到

在等式2-35，这是SNR的最大可能值，因此，我们已经证明了$\mu \widehat{S^{\ast }}$是$\hat{W}$的最佳值。W的最佳值现在可以从(2-22)获得

下面是W的最佳值计算方法，


因此，对于图2-1中的combiner，最优权向量W是满足方程的W值：

最后的输出信噪比的公式如下：

上面这个信噪比公式，是由下面这些公式得来的：

推导到广义信噪比优化

广义信噪比优化通常指的是一种优化过程或算法，旨在通过调整系统的参数或配置，最大化信号与噪声之间的比率。
如果阵列被设计成使权重被自适应地控制以满足(2-42)，则设计者被迫接受SNR作为所有噪声环境的支配标准，包括正常的“静止”环境(无干扰)。然而，大多数应用中，设计者愿意在SNR上妥协，以便获得对图案形状的一些控制，特别是旁瓣电平。
可以按如下方式开发一种易于处理的方法。假设在正常的静态环境中，最期望的阵列权重由权重向量$W_q$。协方差矩阵在正常的环境下是$M_q$。

作者想表达的观点是将$W_q$视为最佳的。

我们希望提出的观点是，在选择W作为最优时，我们实际上已经决定优化到等价的信号向量T而不是实际的信号向量S。如果环境改变，使得协方差矩阵变成M，那么从上一节的结果来看，为了继续在T上优化，应该调整权重，以便下等式成立

因为需要一个比SNR更加通用的标准，所以引入了GSN。GSN相比于SNR考虑了信号和噪声的分布。
GSN本身的数值没有意义。它只在保持向量T不变的比较中才有意义。将固定阵列的GSN与自适应阵列的GSN进行比较是有意义的。然后，假设对于所有噪波环境，权重向量保持为固定的$W_q$,那么GSN是

用（3-1）的公式转换一下，GSN可以被写作

对于自适应天线，GSN是

在正常的静态环境下，GSN可以写作

如果这些噪声在统计上与静止环境中的噪声源无关，我们可以写

其中，$M_j$是由于附加噪声源引起的噪声分量的协方差矩阵。
由以上的公式，我们可以推导出

$(GSN{)}_f$ 指的是在固定权重$(W_q{)}_f$下的广义信噪比，即在正常“静默”环境下的信噪比。在这种情况下，权重$(W_q{)}_f$是预设的，用于在无干扰的环境中获得最优的权衡。

$(GSN{)}_a$指的是在自适应权重$(W_a)$下的广义信噪比。这是在存在干扰的情况下，通过自适应算法实时计算得到的权重，以优化信噪比。