【力扣 - 和为K的子数组】

题目描述

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

提示：

1 <= nums.length <= 2 * 10^4
-1000 <= nums[i] <= 1000
-10^7 <= k <= 10^7

方法一：枚举

思路和算法

考虑以 i 结尾和为 k 的连续子数组个数，我们需要统计符合条件的下标 j 的个数，其中 0≤j≤i且 [j..i] 这个子数组的和恰好为 k 。

我们可以枚举 [0..i]里所有的下标 j来判断是否符合条件，可能有读者会认为假定我们确定了子数组的开头和结尾，还需要 O(n) 的时间复杂度遍历子数组来求和，那样复杂度就将达到 O(n3) 从而无法通过所有测试用例。但是如果我们知道 [j,i] 子数组的和，就能 O(1) 推出 [j−1,i] 的和，因此这部分的遍历求和是不需要的，我们在枚举下标 j 的时候已经能 O(1) 求出 [j,i] 的子数组之和。

代码

/**
 * Function to count the number of subarrays that sum up to the target value k
 * @param nums: array of integers
 * @param numsSize: size of the input array
 * @param k: target sum value
 * @return the number of subarrays that sum up to k
 */
int subarraySum(int* nums, int numsSize, int k) {
    int count = 0; // Initialize the count of subarrays that sum up to k

    // Iterate through each index as the starting point of the subarray
    for(int leftindex = 0; leftindex < numsSize; ++leftindex)
    {
        int sum = 0; // Initialize the sum of the subarray starting at leftindex

        // Calculate the sum of subarrays starting from leftindex and ending at different points
        for(int rightindex = leftindex; rightindex >= 0; --rightindex)
        {
            sum = sum + nums[rightindex]; // Add the element at rightindex to the sum

            // Check if the current sum equals the target value k
            if(sum == k)
            {
                count++; // Increment the count as a subarray with sum k is found
            }
        }
    }
    return count; // Return the total count of subarrays with sum equal to k
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

方法二：前缀和 + 哈希表优化

思路和算法

我们可以基于方法一利用数据结构进行进一步的优化，我们知道方法一的瓶颈在于对每个 i，我们需要枚举所有的 j 来判断是否符合条件，这一步是否可以优化呢？答案是可以的。

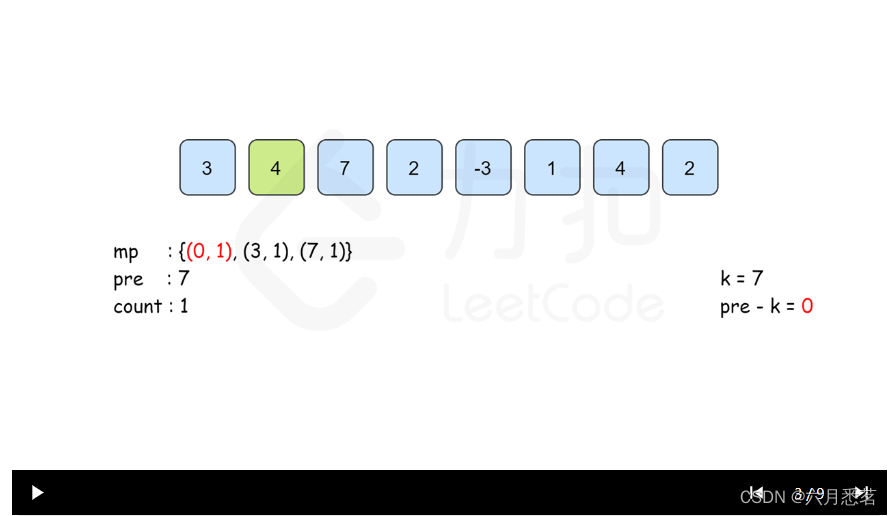
代码

// Structure to represent a node in the hash table
struct Node {
    int key;
    int value;
    struct Node* next;
};

// Function to create a new node for the hash table
struct Node* createNode(int key, int value) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->key = key;
    newNode->value = value;
    newNode->next = NULL;
    return newNode;
}

// Function to count the number of subarrays that sum up to the target value k
int subarraySum(int* nums, int numsSize, int k) {
    // Initialize an array of pointers to nodes for the hash table
    struct Node* map[numsSize + 1];
    for (int i = 0; i <= numsSize; i++) {
        map[i] = NULL;
    }
    
    // Initialize the first node in the hash table
    map[0] = createNode(0, 1);
    int count = 0, pre = 0;
    
    // Iterate through the input array to calculate subarray sums
    for (int i = 0; i < numsSize; i++) {
        pre += nums[i];
        
        // Calculate the key for the current subarray sum
        int key = pre - k;
        int index = (key % (numsSize + 1) + numsSize + 1) % (numsSize + 1); // Ensure non-negative index
        struct Node* current = map[index];
        
        // Traverse the linked list at the computed index
        while (current != NULL) {
            if (current->key == key) {
                count += current->value;
            }
            current = current->next;
        }
        
        // Calculate the new index for the current sum
        int newIndex = (pre % (numsSize + 1) + numsSize + 1) % (numsSize + 1); // Ensure non-negative index
        if (map[newIndex] == NULL) {
            map[newIndex] = createNode(pre, 1);
        } else {
            struct Node* temp = map[newIndex];
            while (temp->next != NULL) {
                temp = temp->next;
            }
            temp->next = createNode(pre, 1);
        }
    }
    
    return count;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

方法三：哈希表（不超时）

前面两个方法都超时了。
利用malloc动态开辟一个数组空间，作为哈希表，数组下标代表哈希key值，数组下标对应的值代表key值指向的元素值，再对数组求前缀和，将前缀和将key值存入哈希数组中，前缀和 p[i] - p[j] = k 就表示数组i - j 满足要求，即p[i] - k = p[j]，每次求出当前前缀和，就在哈希数组中判断是否存在p[j]，累加p[j]存在个数，并返回

// Function to count the number of subarrays that sum up to the target value k
int subarraySum(int *nums, int numsSize, int k) {
    int count = 0;
    
    // Create a large array to act as a simple hash table, initialized to all zeros
    int *maps = (int *)calloc(10000001 * 2, sizeof(int));
    
    // Set the pointer to the middle position to accommodate negative prefix sums
    int *map = maps + 10000001 * 1;
    
    // Initialize the prefix sum with an additional sum at index 0
    int sum = 0;
    map[sum]++;
    
    // Calculate prefix sums and count subarrays with target sum k
    for (int i = 0; i < numsSize; i++) {
        sum += nums[i];
        
        // Check if a previous prefix sum exists that can form a subarray with sum k
        if (map[sum - k] > 0) {
            count += map[sum - k];
        }
        
        // Update the count of prefix sums encountered
        map[sum]++;
    }
    
    // Free the memory allocated for the hash table array
    free(maps);
    
    return count;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32