【MATLAB】 小波分解信号分解+FFT傅里叶频谱变换组合算法

有意向获取代码，请转文末观看代码获取方式~

展示出图效果

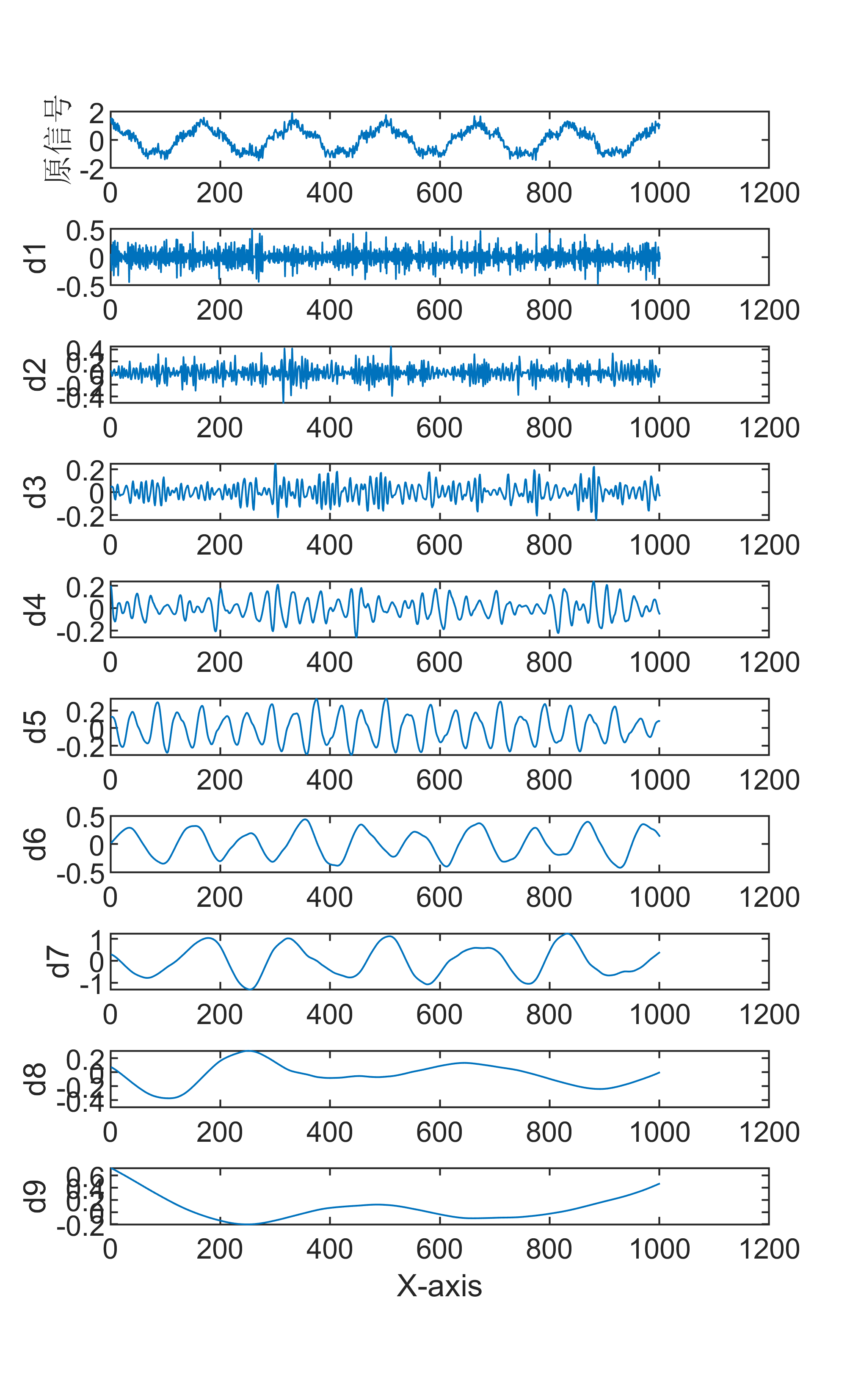
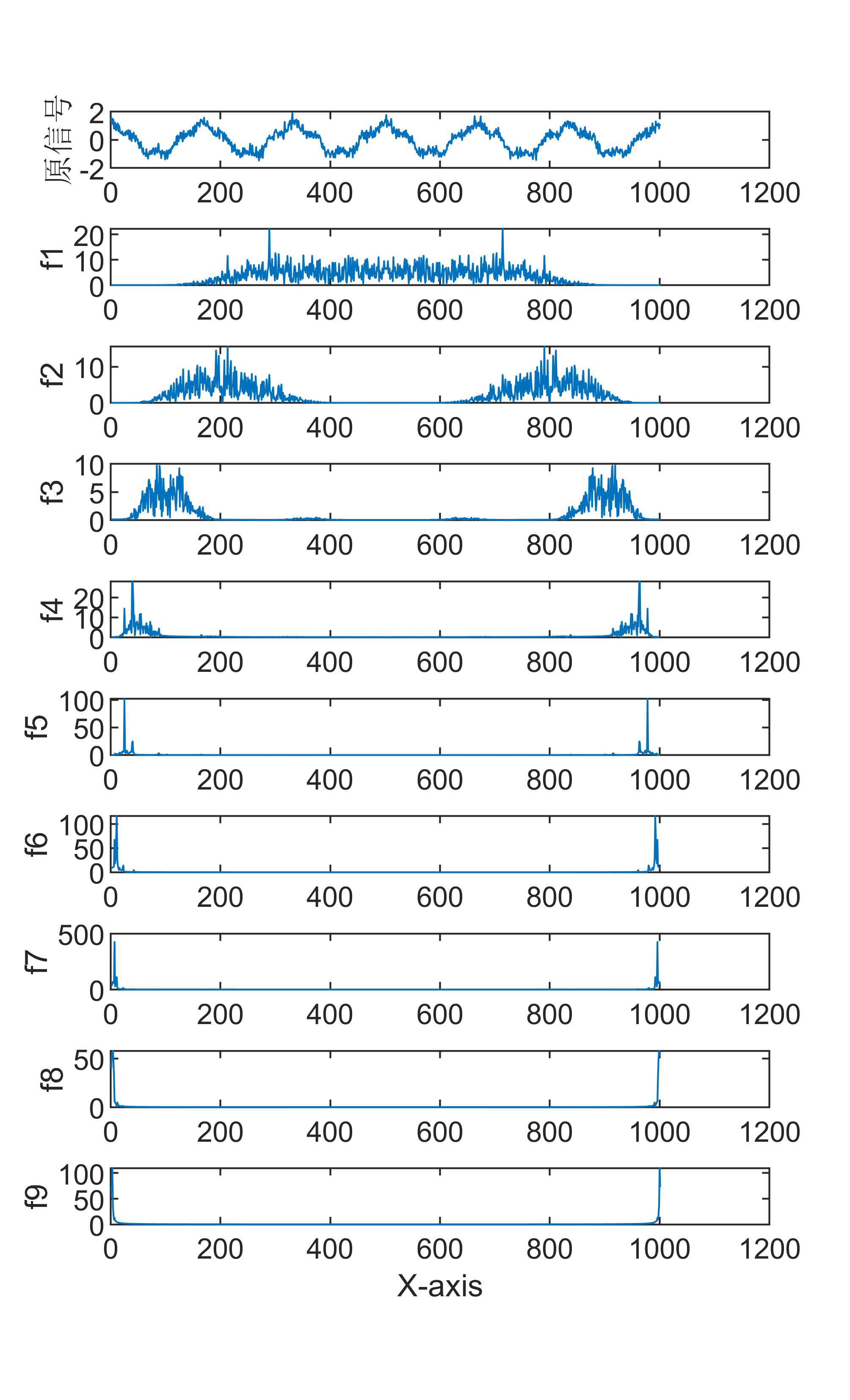
1 小波分解算法

小波分解算法是一种数学方法，用于将信号分解为不同频率的小波成分。这种算法基于小波函数，可以用于信号处理、图像压缩和数据压缩等领域。小波分解算法的基本思想是将一个信号分解成多个小波子带，每个小波子带代表了一个不同频率的小波成分。这些小波子带可以分别进行处理，例如滤波、降采样等操作，然后再进行重构，得到原始信号。小波分解算法的优点是可以提供更好的时频分辨率，对于瞬态信号和非平稳信号的处理效果更好。同时，小波分解算法也可以用于图像压缩和数据压缩，因为小波分解后的子带可以选择性地保留或舍弃，从而实现数据压缩。总之，小波分解算法是一种强大的信号处理技术，被广泛应用于信号处理、图像压缩和数据压缩等领域。

关于简短的代码视频教程均可关注B站、小红书、知乎同名账号（Lwcah）观看教程~

MATLAB 信号分解第六期-小波分解:

信号分解全家桶详情请参见：

2 FFT傅里叶频谱变换算法

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

MATLAB | 频谱分析算法 | 傅里叶变换 开源 MATLAB 代码请转:

MATLAB | 9种频谱分析算法全家桶详情请参见：

3 小波分解信号分解+FFT傅里叶频谱变换组合算法

如下为简短的视频操作教程。

【MATLAB 】小波分解信号分解+FFT傅里叶频谱变换组合算法请转:

【MATLAB 】信号分解+FFT傅里叶频谱变换组合算法全家桶详情请参见：

关于代码有任何疑问，可以一起探讨科研，写作，代码等诸多学术问题，我们一起进步~

---

代码见附件~