LeetCode之二叉树

发现新天地，欢迎访问Cr不是铬的个人网站

平衡二叉树

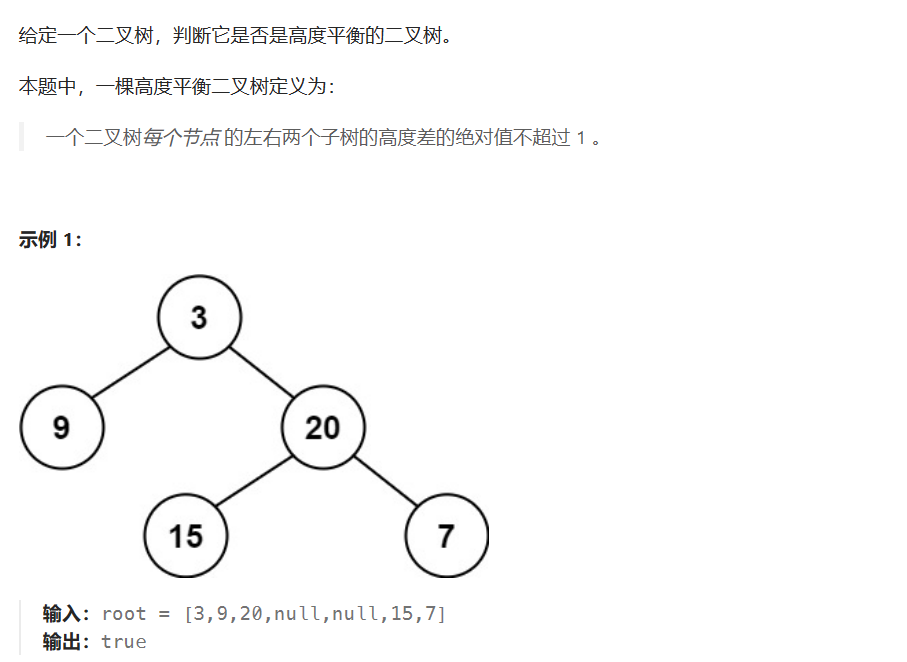
做这一道题目我们要考虑到平衡二叉树的定义。也就是一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 关于一个结点的高度计算我们很容易用递归得出，那么我们用递归遍历加上这个判断条件即可.

class Solution {
public:
    int getHeight(TreeNode*root)
    {
        if(root == nullptr)return 0;
        return max(getHeight(root->left),getHeight(root->right)) + 1;
    } 
    bool isBalanced(TreeNode* root) {
        if(root == nullptr)
            return true;
        return abs(getHeight(root->left) - getHeight(root->right))<=1 && isBalanced(root->left)&&isBalanced(root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

二叉树的最小深度

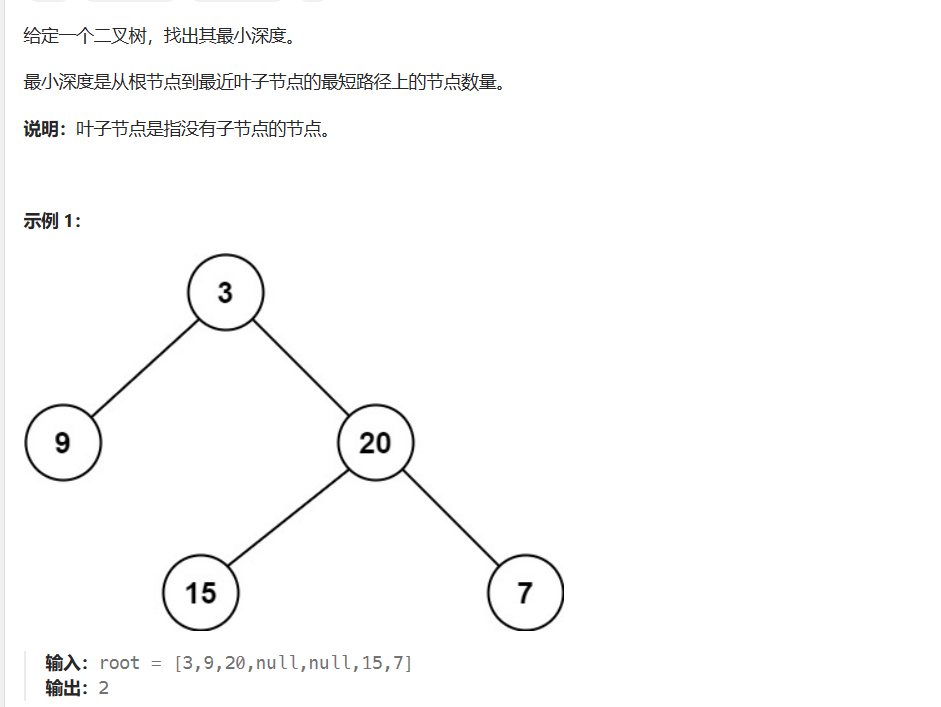上面一题我们讲的是关于高度，这个题就是求最小的深度。 关于这个题我们划分有三种情况

• root为空，直接返回0
• root->left和root->rigth中有一个为空，我们只要返回不为0的那个深度+1就行
• roo->left与root->rigth都不为空，直接返回两者较小的+1

代码:

class Solution {
   public:
        int minDepth(TreeNode root) {
        if(root == null) return 0;
        //1.左孩子和有孩子都为空的情况，说明到达了叶子节点，直接返回1即可
        if(root.left == nullpter && root.right == nullpter) return 1;
        //2.如果左孩子和由孩子其中一个为空，那么需要返回比较大的那个孩子的深度        
        int m1 = minDepth(root.left);
        int m2 = minDepth(root.right);
        //这里其中一个节点为空，说明m1和m2有一个必然为0，所以可以返回m1 + m2 + 1;
        if(root.left == null || root.right == null) return m1 + m2 + 1;

        //3.最后一种情况，也就是左右孩子都不为空，返回最小深度+1即可
        return min(m1,m2) + 1; 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

本文由博客一文多发平台 OpenWrite 发布！