卡尔曼滤波器的推导

参考资源

【卡尔曼滤波器】1_递归算法_Recursive Processing_哔哩哔哩_bilibili

【卡尔曼滤波器】2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题_哔哩哔哩_bilibili

【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ～全网最完整_哔哩哔哩_bilibili

【卡尔曼滤波器】4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式_哔哩哔哩_bilibili

【卡尔曼滤波器】5_直观理解与二维实例【包含完整的EXCEL代码】_哔哩哔哩_bilibili

说明

我是跟着DR_CAN老师几篇视频的讲解，自己推导了一遍，加深理解，也方便查阅。老师讲得很好。

Kalman filter is an optimal recursive data processing algorithm.

卡尔曼滤波器是一个最优的、递归的数据处理算法，可以对输入数据进行时间递归处理。它是一个线性滤波器。

数据预测具有不确定性，数据测量也有不确定性，卡尔曼滤波是根据不那么准确的预测模型、和不那么准确的观测，来拟合出一个最优值。

递归算法

假设用一把尺子对一个物体进行测量，测了k次，测量值分别是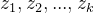现在求估计值。

测量了k次的估计值为：

上式表达的意思是：

当前的估计值 = 上次的估计值 + 系数 *（当前的测量值 – 上次的估计值）

在卡尔曼滤波器中， 是卡尔曼增益（Kalman Gain）。

定义估计误差和测量误差：

估计误差：代表估计值和真实值的差距

测量误差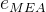：代表测量值和真实值的差距

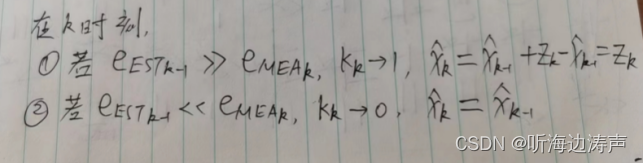
手工计算前面几次：

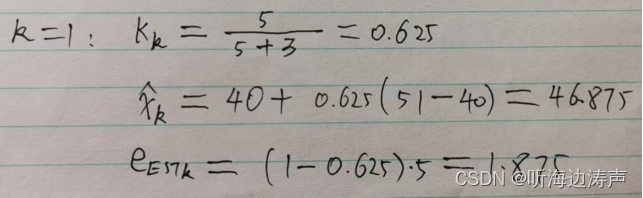
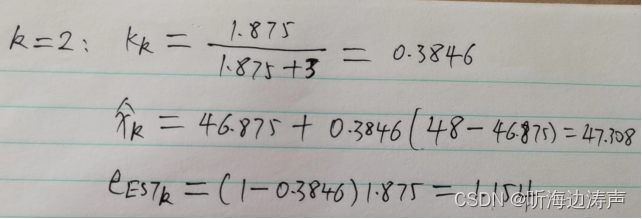
用excel计算：

根据excel计算结果画的图：

数学基础：数据融合、协方差矩阵、状态空间方程

数据融合

例如用两个称称一个物体，两个称都不准。

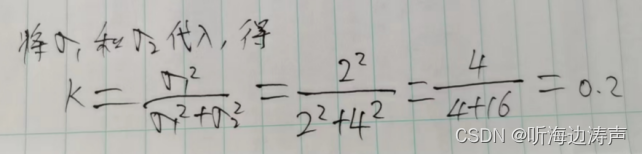
协方差矩阵

协方差矩阵，将方差、协方差在一个矩阵中表现出来，体现了变量间的联动关系。

例子：

协方差：

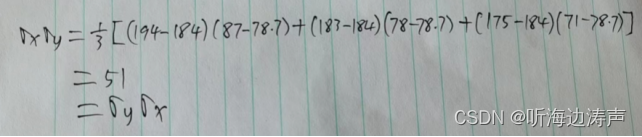
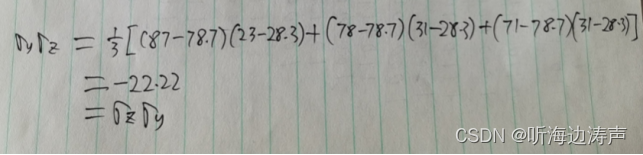
协方差矩阵：

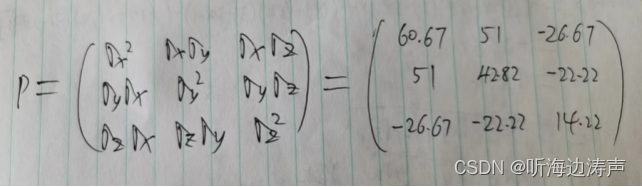
定义矩阵：

则，协方差矩阵：

更多球员的数据：

求出的协方差矩阵是：

状态空间表达

将上面四个方程，用矩阵形式表示出来，作为状态空间方程：

卡尔曼增益的数学推导

假设噪声符合正态分布：

其中上式中E表示期望。

下面证明：

如果X的期望为0，即E(X)=0，那么

因为假设噪声符合期望为0的高斯分布，所以：

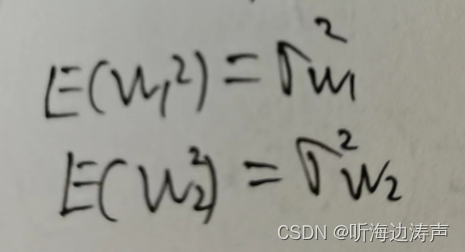
定义后验估计误差：

下面计算协方差矩阵P：

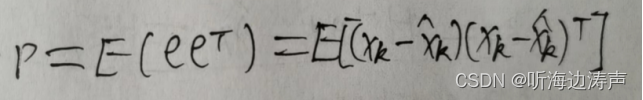
进一步提取：

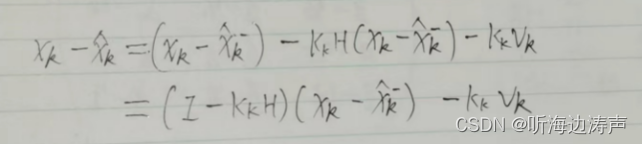
定义先验估计误差：

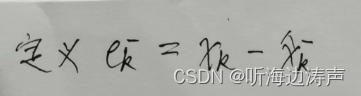
可得：

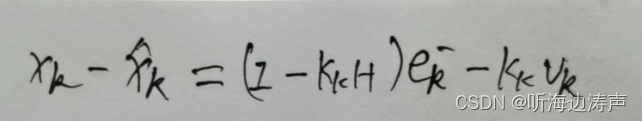
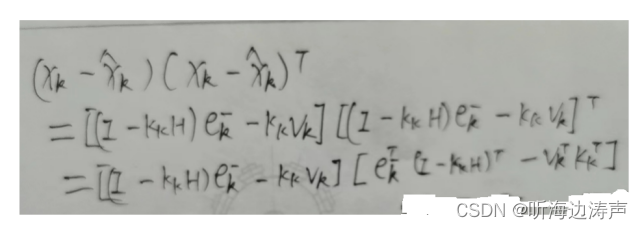
得到后验估计误差的协方差矩阵：

目标是使后验估计误差协方差矩阵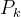的迹（trace）最小。

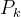的迹：

因为一个矩阵和它的转置矩阵的迹相同，所以：

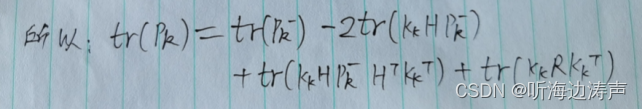
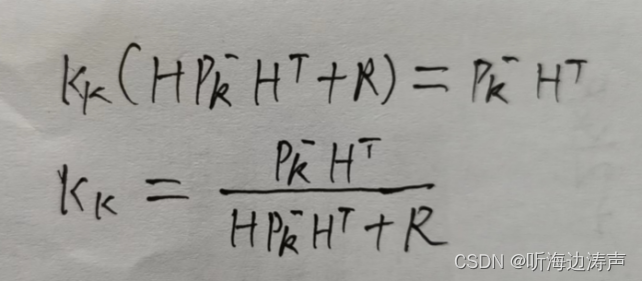
上式就是卡尔曼增益的公式，是卡尔曼滤波中的一个核心公式。

其中R是测量误差的协方差矩阵。

当R很大的时候，即测量误差很大的时候，

由上面的公式：

可知，此时的后验估计值等于先验估计：

当R很小，即测量误差很小的时候：

此时的估计值等于测量值：

误差协方差矩阵

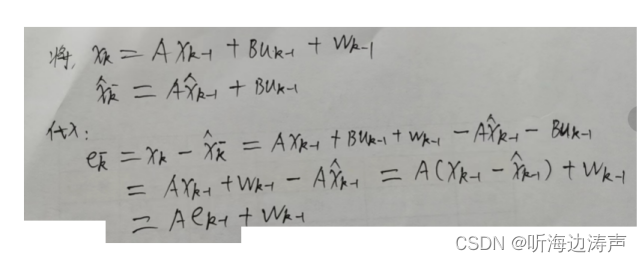
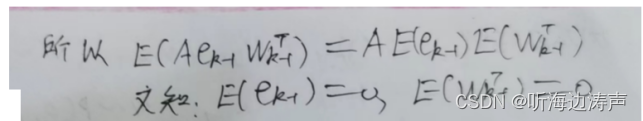
卡尔曼滤波器的5个公式：

在卡尔曼增益公式推导过程中，我们已经得出：

通过一个二维实例直观理解卡尔曼滤波器

 

考虑一个人走路，假设匀速行驶。分别设定两个状态变量：

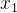：表示位置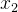

：表示速度

此时，速度和位置状态方程变为：

因为加上了不确定性，所以就无法直接通过上面两个式子求出k时刻的位置、速度。但是可以估计，根据噪声的误差来估计。

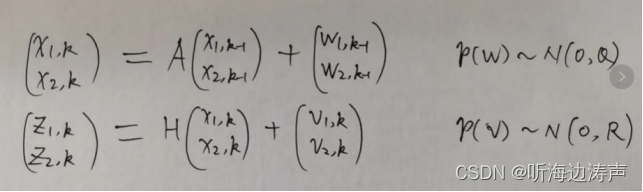
卡尔曼滤波器分两个步骤：预测和校正：

用excel计算：

为了简化起见，设Q矩阵、R矩阵的协方差项为0，即各误差项之间是相互独立的。所以Q矩阵和R矩阵只有对角线上的值不等于0。矩阵的值自己可以修改