算法通关村第九关-青铜挑战二分查找算法

大家好我是苏麟 ,  今天聊聊二分查找算法 ......

普通查找

普通查找就是最简单的循环查找 , 无论是有席的还是无席的都可以，也不需要排序，只需要一个个对比即可，但其实效率很低 :

    public int search(int[] arr, int target) {
        for (int i = 0; i < arr.length; i++) {
            if (target == arr[i]) {
                return i;
            }
        }
        return -1;
    }

顺序查找是最简单的一种查找算法，对数据的要求也很随意，不需要排序即可查找。

二分查找

分查找就是将中间结果与目标进行比较，一次去掉一半 .

二分查找的原理

为什么说二分查找的效率最高呢？因为每一次选择数字，无论偏 大还是偏小，都可以让剩下的选择范围缩小一半。

给定范围0到1000的整数：

第一次我们选择500，发现偏大了，那么下一次的选择范围，就变 成了0到499：

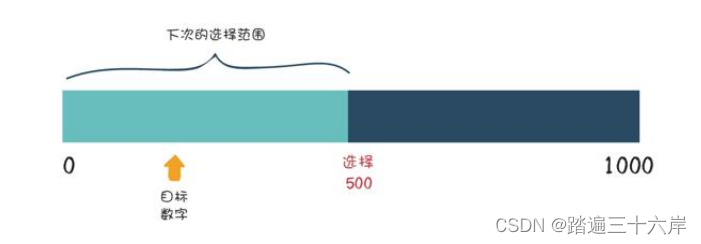
第二次我们选择250，发现还是偏大了，那么下一次的选择范围， 就变成了0到249：

以此类推，最坏的情况需要猜测多少次呢？答案是 log1000 = 10 次，也就是让原本的区间范围进行10次“折半”。

二分查找最基础代码

二分查找，我觉得应该达到闭着眼睛就能写出来，一分钟就能写出来的地步.

    /**
     * 基础版
     *
     * @param arr
     * @param x
     * @return
     */
    public static int algorithm(int[] arr, int x) {
        int left = 0;
        int right = arr.length - 1;
        //  i<=j   如果只有一个元素的时候
        while (left <= right) {
            // >>> 数字很大的时候
            int min = (left + right) / 2;
 
            if (x < arr[min]) {
                right = right - 1;
            } else if (arr[min] < x) {
                left = min + 1;
            } else {
                return min;
            }
        }
        return -1;
    }

在具体操作的时候可能有多种方式的，包括循环体中的 high = mid -1;和low = mid + 1也有多种方式的，这需要与if后面的条件配合，我们不要给自己添麻烦，在理解的基础上熟记这种方式就行了。

改动版

虽然只改动一个部分但是有很大作用 , 因为上面那只种方式当left和right相加大于int最大值时会溢出 .

    /**
     * 基础版
     *
     * @param arr
     * @param x
     * @return
     */
    public static int algorithm(int[] arr, int x) {
        int left = 0;
        int right = arr.length - 1;
        //  i<=j   如果只有一个元素的时候
        while (left <= right) {
            // >>> 数字很大的时候
            int min = (left + right) >>> 1;
 
            if (x < arr[min]) {
                right = right - 1;
            } else if (arr[min] < x) {
                left = min + 1;
            } else {
                return min;
            }
        }
        return -1;
    }

小题一道 : 二分查找

题目 :

LeetCode 704.二分查找

704. 二分查找

 这道题一定要做啊 , 不仅做还要能闭着眼睛做 .

元素中有重复的二分查找

假如在上面的基础上，元素存在重复，如果重复则找左侧第一个，请问该怎么做呢? 
这里的关键是找到目标结果之后不是返回而是继续向左侧移动。

 /**
     * Leftmost  如果有相等的数返回最左边的
     *
     * @param arr
     * @param x
     * @return
     */
    public static int algorithmLeftMost(int[] arr, int x) {
        int left = 0;
        int right = arr.length - 1;
        int candidate = -1;
        //  i<=j   如果只有一个元素的时候
        while (left <= right) {
            // >>> 数字很大的时候
            int min = (left + right) >>> 1;
 
            if (x < arr[min]) {
                right = right - 1;
            } else if (arr[min] < x) {
                left = min + 1;
            } else {
                candidate = min;
                right = min - 1;
            }
        }
        return candidate;
    }

小伙伴们思考思考 ......

这期就到这里 下期见!