
本文从概念、原理、距离函数、K 值选择、K 值影响、、优缺点、应用几方面详细讲述了 KNN 算法
K 近临(K Nearest-Neighbours)
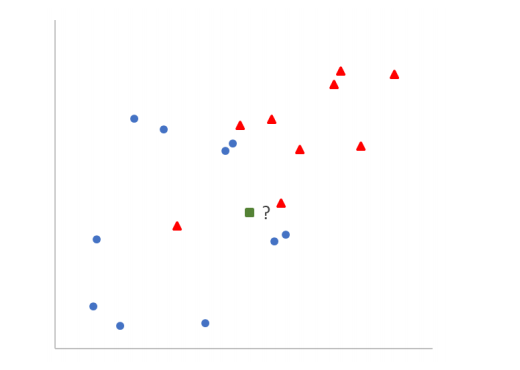
一种简单的监督学习算法,惰性学习算法,在技术上并不训练模型来预测。适用于分类和回归任务。它的核心思想是:相似的对象彼此接近。例如,若果你想分类一个新的数据点(绿点),可以查看训练数据中哪些数据点与它最接近,并根据这些最接近的数据点和标签来预测它的标签(红点或蓝圆)。

概念
K: 这是一个用户指定的正整数,即训练数据分类数量,代表要考虑的最近邻居的数量,上图中假设 K=2,即训练数据分类为蓝色圆和红色三角两类标签。
距离函数: 用于计算数据点之间的距离。最常见的是欧几里得距离、曼哈顿距离、马氏距离等。
投票机制:
- 分类任务: 将根据 k 个最近邻的多数投票来确定新数据点的类别。
- 回归任务: 通常取 k 个最近邻的输出变量的平均值。
原理
- 距离计算: 对于给定的新数据点,计算它与训练数据集中每个点的距离。
- 选取 K 个邻居: 从训练数据集中选取距离最近的 K 个点。
- 投票 (对于分类): 对于 K 个邻居,看哪个类别最为常见,并将其指定为新数据点的类别。
- 均值 (对于回归): 对于 K 个邻居,计算其属性的平均值,并将其指定为新数据点的值。
距离度量
欧几里得距离 (Euclidean Distance)
欧几里得距离的名称来源于古希腊数学家欧几里得,是衡量两点在平面或更高维空间中的"直线"距离。它基于勾股定理,用于计算两点之间的最短距离。在日常生活中,我们经常无意识地使用欧几里得距离,例如,当我们说两地之间的"直线"距离时,实际上是在引用欧几里得距离。
公式:
给定两点 P 和 Q,其坐标分别为 P(x1,x2,...,xn) 和 Q(y1,y2,...,yn) 在一个 n 维空间中,它们之间的欧几里得距离 d 定义为:
d(P,Q)=√∑ni=1(xi−yi)2
曼哈顿距离 (Manhattan Distance)
曼哈顿距离得名于纽约的曼哈顿,因为在曼哈顿的街道布局是网格状的。想象一下,你在一个街区的一个角落,要走到对面的角落,你不能直接穿越街区,只能沿着街道走。这就是曼哈顿距离的来源,也因此它有时被称为“城市街区距离”。
公式
给定两点 P 和 Q,其坐标分别为 P(x1,x2,...,xn) 和 Q(y1,y2,...,yn) 在一个 n 维空间中,它们之间的曼哈顿距离 L1 定义为:
L1(P,Q)=∑ni=1|xi−yi|
闵可夫斯基距离 (Minkowski Distance)
闵可夫斯基距离是一种在向量空间中度量两个点之间距离的方法。它实际上是一种泛化的距离度量,可以看作是其他距离度量(如欧几里得距离、曼哈顿距离)的泛化。通过改变一个参数p,它可以表示多种距离度量。
公式
给定两点 P 和 Q,其坐标分别为 P(x1,x2,...,xn) 和 Q(y1,y2,...,yn) 在一个 n 维空间中,它们之间的闵可夫斯基距离 Lp 定义为:
Lp(P,Q)=(∑ni=1|xi−yi|p)1p
其中 p 是一个大于等于 1 的实数。特定的 p 值会导致其他常见的距离度量:
- 当
p = 1时,这变成了曼哈顿距离。 - 当
p = 2时,这变成了欧几里得距离。
余弦相似性 (Cosine Similarity)
余弦相似性度量了两个向量方向的相似度,而不是它们的大小。换句话说,它是通过比较两个向量之间的夹角来测量它们的相似性的。夹角越小,相似性就越高。
它经常在高维空间中(如 TF-IDF 权重的文档向量)使用,因为在高维空间中,基于欧几里得距离的相似性度量可能不太有效。
公式
给定两个向量 A 和 B,它们的余弦相似性定义为:
cosine similarity(A,B)=A⋅B‖
其中:
- A \cdot B 是向量
A和B的点积。 - \|A\| 和 \|B\| 分别是向量
A和B的欧几里得长度(或模)。
公式可以进一步扩展为:
\text{cosine similarity}(A, B) = \frac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \sqrt{\sum_{i=1}^{n} B_i^2}}
这里,n 是向量的维度,而 A_i 和 B_i 分别是向量 A 和 B 在第 i 维度上的值。
余弦相似性值范围为[-1, 1],其中 1 表示完全相似,0 表示不相关,而-1 表示完全相异。
K 值的确定方法:
-
交叉验证: 这是确定 k 值的最常用方法。对于每一个可能的 k 值,使用交叉验证计算模型的预测错误率,选择错误率最低的 k 值。
-
启发式方法: 有时,可以选择 sqrt(n)作为起始点,其中 n 是训练样本的数量。这只是一个粗略的估计,通常需要进一步验证。
-
误差曲线: 画出不同 k 值对应的误差率曲线,选择误差变化开始平稳的点。
-
领域知识: 在某些应用中,基于领域知识和经验选择 k 值可能更为合适。
K 值的影响:
过小的 k 值:
- 分类:模型可能变得过于敏感和复杂。它可能对训练数据中的噪声或异常点特别敏感,从而容易过拟合。当 k=1 时,任何训练数据中的异常点都可能影响预测结果。
- 回归:模型可能会受到异常值的强烈影响,导致预测结果出现明显的波动。
过大的 k 值:
- 分类:模型可能变得过于简化。随着 k 值的增加,分类决策的边界会变得更加平滑,可能会忽视数据中的细微模式,导致欠拟合。
- 回归:模型同样可能会过于简化。大 k 值使模型的预测偏向于所有数据点的平均值,因此可能会忽视数据中的局部特性或细节。
优缺点
优点
简单且直观。
无需训练阶段,适用于动态变化的数据集。
对异常值不敏感(取决于 K 的大小)。
缺点
计算复杂度高,因为对于每一个新的数据点,都需要与所有训练数据计算距离。
需要决定 K 的大小,这可能会影响结果。
高维数据中的性能下降。
应用场景:
-
推荐系统:
- 基于用户之前的喜好推荐相似电影
- 推荐用户可能喜欢的曲目或歌手
-
文本分类:
区分垃圾邮件和正常邮件。 -
图像识别: 识别包括上的手写邮政编码,分类投递邮件包裹
-
医疗诊断: 预测患者可能的疾病风险。
-
信用评分:预测客户的信用风险。
-
欺诈检测:识别信用卡中的异常交易。
-
位置基服务:基于位置提供餐厅或服务推荐。