第一讲之递推与递归上篇

本专栏博客，根据acwing中蓝桥杯C++AB组辅导课编写

数据与算法的关系

简单斐波那契

简单斐波那契

斐波那契数列的话，只要掌握规律，就比较好解决了
0 1 1 2 3 5 8 13…

第一项是0.第二项为1，从第三项开始，下一项等于前2项之和

1. 递归方式

#include
#include

using namespace std;

 int  fib(int n)
 {
    if(n == 1)
    {
        return 0;
    }
    else if(n == 2)
    {
        return 1;
    }
    else if(n >= 3)
    {
        return fib(n - 1) + fib(n - 2);
    }
    
   
 }
 

int main()
{
    int N;
    cin >> N;
    
    for(int i = 1;i <= N; i++)
    {
        cout << fib(i) << " ";
    }
        
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

但是这种方式递归，递归的次数太多，导致时间超时

2.保留下一项的数，来进行优化 以及递推
（使用滚动数组来进行优化）

#include
#include
#include

using namespace std;

int main()
{
    int N;
    cin >> N;
    
    int a = 0;
    int b = 1;
    
    for(int i = 0; i < N ;i++)
    {
        cout << a << " ";
        int c = a + b;
        a = b;
        b = c;
    }
    
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

递归实现指数型枚举

递归实现指数型枚举

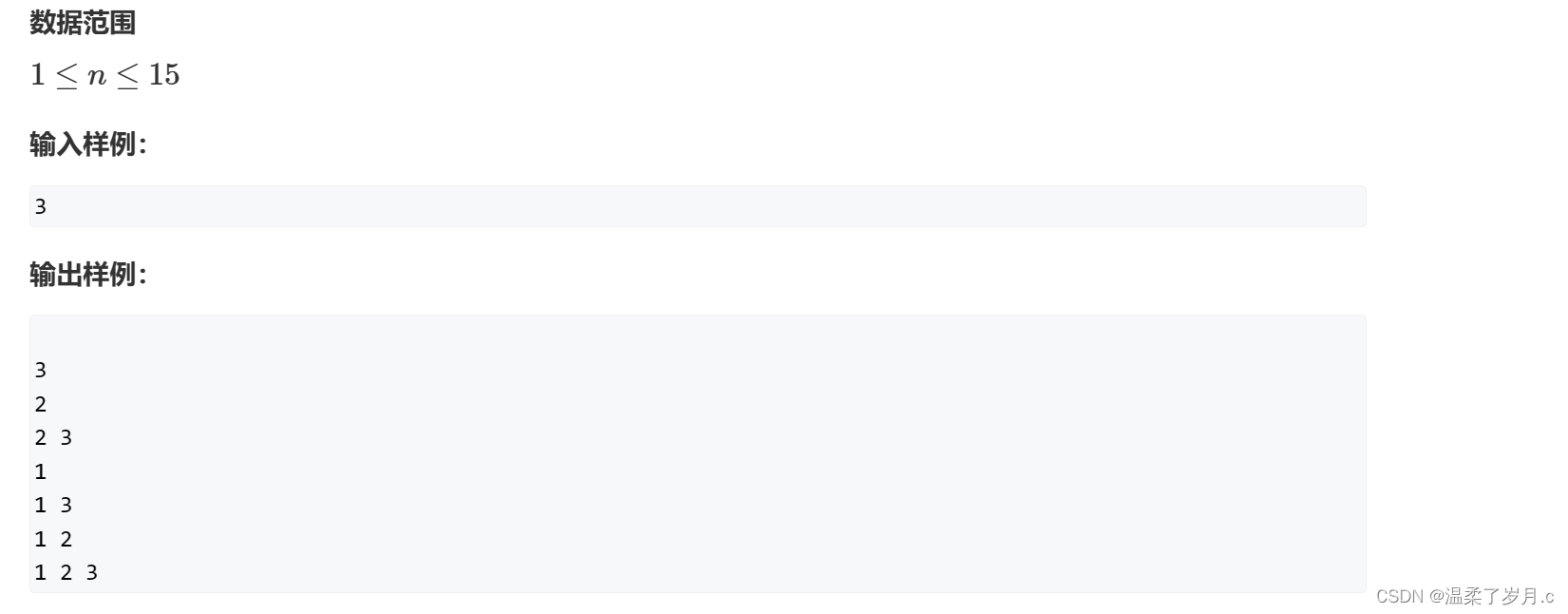
首先，给大家解释一下，为什么这个叫指数型枚举
根据对这个输入样例和输出样例的观察
数有2种可能性，选与不选，
n个数的话
一组数据，就是 2 * 2 * 2 * 2 * 2 … ----> 2^n种可能性
所有数都输出，每一组数据的长度为n（考虑最坏的情况）
所以，时间复杂度是 n * 2 ^ n

这里采用dfs进行枚举实现

#include
#include
#include

using namespace std;

//数据范围15, 从1开始算

const int N = 16;  //记录数

//一个数有2个状态，选 1 或者 不选 0 
//用2对每个数进行初始化，表示还没有考虑这个数

int map[N]; //记录数的状态， 初始状态都为2
int u;

void dfs(int n)
{
    //数从1开始，这里下标，我也从1开始

    //结束递归条件
    if(n > u)
    {
        for(int i = 1; i <= u; i++ )
        {
            if(map[i] == 1)
            {
                printf("%d ", i);
            }
        }

        printf("\n");

        return;  //注意这步，退出这个递归， 这步不要忘记

    }

    map[n] = 1; //表示第一分支， 选这个数
    dfs(n + 1);
    map[n] = 2; //恢复现场

    map[n] = 0; //表示第二个分支，不选这个数
    dfs(n + 1);
    map[n] = 2;  //恢复现场 (这步其实可以不用)

}

int main()
{

    cin >> u;

    dfs(1);

    return 0;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

递归实现排列型枚举

做这题之前，我们要知道什么是字典序。
字典序：在计算机中是用来比较任意两个字符串的大小，也就是比较字符串的ASCII码的大小。

这里两种方式;
1.枚举位置
2.枚举数

当然，我这里选择枚举位置

//两种方式，
// 1.枚举数
// 2. 枚举位置

//这里用的方式2，枚举位置
#include
using namespace std;

const int N = 10;
int n;        
int path[N];   //存储数据
bool used[N];  //状态数组

void dfs(int u)
{
    if(u > n)
    {
        for(int i = 1; i <= n; i++)
        {
            if(used[i])  //这个判断，可加，可不加，因为每个数都要输出
            {
                
            cout << path[i] << " ";
            }
            
            
        }
        
        cout << endl;
        return;
    }
    
    for(int i = 1; i <= n; i++)
    {
        if(!used[i])
        {
            used[i] = true; //这个数被使用
            path[u] = i;  //这个位置枚举
            
            dfs( u + 1);   //枚举下一个位置
            
            //恢复现场
            used[i] = false;
            path[u] = 0;
        }
    }
}

int main()
{
    cin >> n;
    
    dfs(1);
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

递归实现组合型枚举

递归的话，要学会自己构建递归树
这里是枚举位置，一共有三个位置
这里按照：从小到大的顺序排列：
就要保证：每一个新加的数要大于前一个数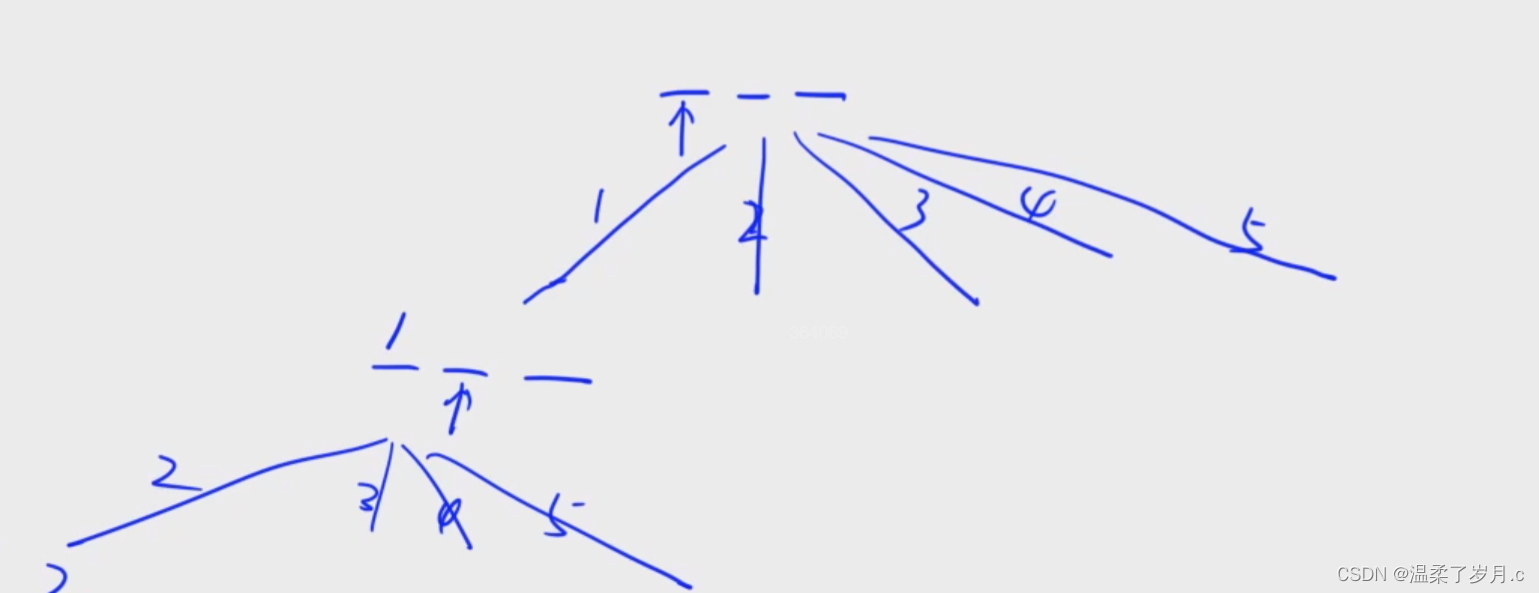

用dfs，要考虑dfs的参数有哪些

这里需要有三个参数
1.一共有位置的多少 （也就是选几个数）(这个一般为全局变量，可以不当做参数)
2.枚举的当前位置
3.从那个数开始枚举

这个dfs也可以认为有2个参数

#include

using namespace std;

const int N = 30;
int n, m;
int way[N];

void dfs(int u, int start)
{
	 //剪枝
    if(u + n- start < m) return;   //如果把后面的数(n - start)，都选上，都不够m个数，那么一定无解
    
    if(u == m + 1)
    {
        for(int i = 1; i <= m; i++) //打印数据（枚举位置）
        {
            cout << way[i] << " ";
        }
        cout << endl;
        
        return;  //退出函数，这步别忘记
    }
    
    for(int i = start; i <= n;i++) //枚举数
    {
        way[u] = i; //存储数据
        
        dfs(u + 1, i + 1);
        
        way[u] = 0;//恢复现场
    }
}
int main()
{
    cin >> n >> m;
    dfs(1, 1); //（第一个参数枚举当前位置，第二个参数枚举数）
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

当然，这里用剪枝对dfs进行了优化

本篇博客，讲解了常见的几种枚举类型，指数型，排列型，组合型。