Python算法练习 10.15

leetcode 2130 链表的最大孪生和

在一个大小为 n 且 n 为 偶数 的链表中，对于 0 <= i <= (n / 2) - 1 的 i ，第 i 个节点（下标从 0 开始）的孪生节点为第 (n-1-i) 个节点 。

• 比方说，n = 4 那么节点 0 是节点 3 的孪生节点，节点 1 是节点 2 的孪生节点。这是长度为 n = 4 的链表中所有的孪生节点。

孪生和 定义为一个节点和它孪生节点两者值之和。

给你一个长度为偶数的链表的头节点 head ，请你返回链表的 最大孪生和 。

示例 1：

输入：head = [5,4,2,1]
输出：6
解释：
节点 0 和节点 1 分别是节点 3 和 2 的孪生节点。孪生和都为 6 。
链表中没有其他孪生节点。
所以，链表的最大孪生和是 6 。

示例 2：

输入：head = [4,2,2,3]
输出：7
解释：
链表中的孪生节点为：
- 节点 0 是节点 3 的孪生节点，孪生和为 4 + 3 = 7 。
- 节点 1 是节点 2 的孪生节点，孪生和为 2 + 2 = 4 。
所以，最大孪生和为 max(7, 4) = 7 。

先用快慢指针找到表中点，从中点开始用头插法，反转表的后半部分，最后从头开始遍历两个表，记录最大和即可。

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def pairSum(self, head):
        """
        :type head: Optional[ListNode]
        :rtype: int
        """
        head = ListNode(0, head)
        fast = slow = head.next
        while fast != None:
            slow = slow.next
            fast = fast.next.next
        reverseHead = ListNode(0, None)
        slowPre = slow
        while slow != None:
            slowPre = slowPre.next
            slow.next = reverseHead.next
            reverseHead.next = slow
            slow = slowPre
        node1 = head.next
        node2 = reverseHead.next
        maxVal = 0
        while node1 and node2:
            maxVal = max(node1.val + node2.val, maxVal)
            node1 = node1.next
            node2 = node2.next
        return maxVal

 leetcode 104 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

 简单的前序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def goNextLevel(root, depth):
            depthLeft = depthRight = depth
            if root:
                depth += 1
                depthLeft = goNextLevel(root.left, depth)
                depthRight = goNextLevel(root.right, depth)
            return max(depthLeft, depthRight)
        depth = 0
        if not root:
            return 0
        else:
            maxdepth = goNextLevel(root, depth)
        return maxdepth

leetcode 872 叶子相似的树

请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。

如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。

如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

 

示例 1：

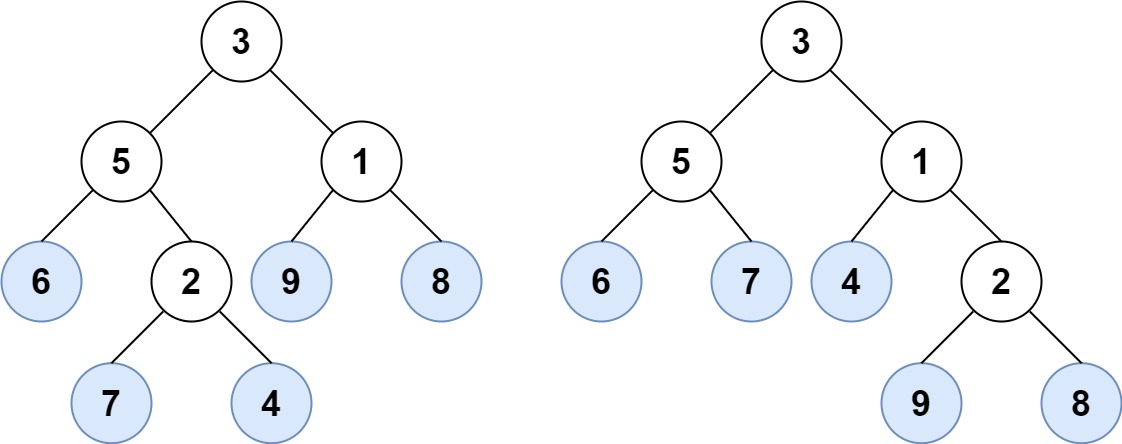
输入：root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
输出：true

示例 2：

输入：root1 = [1,2,3], root2 = [1,3,2]
输出：false

 本质就还是前序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def leafSimilar(self, root1, root2):
        """
        :type root1: TreeNode
        :type root2: TreeNode
        :rtype: bool
        """
        def goNextLevel(root, LeafArr):
            if not root.left and not root.right:
                LeafArr.append(root.val)
                return
            if root.left:
                goNextLevel(root.left, LeafArr)
            if root.right:
                goNextLevel(root.right, LeafArr)      
        root1LeafArr = []
        root2LeafArr = []
        if root1:
            goNextLevel(root1, root1LeafArr)
        if root2:
            goNextLevel(root2, root2LeafArr)
        return root1LeafArr == root2LeafArr

 leetcode 1448 统计二叉树中好节点的数目

给你一棵根为 root 的二叉树，请你返回二叉树中好节点的数目。

「好节点」X 定义为：从根到该节点 X 所经过的节点中，没有任何节点的值大于 X 的值。

 

示例 1：

输入：root = [3,1,4,3,null,1,5]
输出：4
解释：图中蓝色节点为好节点。
根节点 (3) 永远是个好节点。
节点 4 -> (3,4) 是路径中的最大值。
节点 5 -> (3,4,5) 是路径中的最大值。
节点 3 -> (3,1,3) 是路径中的最大值。

示例 2：

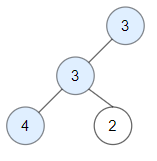
输入：root = [3,3,null,4,2]
输出：3
解释：节点 2 -> (3, 3, 2) 不是好节点，因为 "3" 比它大。

 递归函数忘了写最后一句return，导致goodNum总是None

还是前序遍历，没什么好说的

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def goodNodes(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        # 记录从根节点遍历到该叶子节点的最大值，如果这个最大值不大于叶子节点的值，就是好节点
        def goNextLevel(root, goodNum, maxVal):
            if maxVal <= root.val:
                goodNum += 1
            if not root.left and not root.right:
                return goodNum
            maxVal = max(maxVal, root.val) 
            if root.left:
                goodNum = goNextLevel(root.left, goodNum, maxVal)
            if root.right:
                goodNum = goNextLevel(root.right, goodNum, maxVal)
            return goodNum
        goodNum = 0
        maxVal = root.val
        if not root:
            return goodNum
        else:
            return goNextLevel(root, goodNum, maxVal)