排序算法一 直接插入排序,希尔排序,直接选择排序,堆排序和冒泡排序

目录

什么是排序

插入排序

直接插入排序

希尔排序(缩小增量排序）

选择排序

直接选择排序

堆排序

交换排序

冒泡排序

---

什么是排序

排序：排序就是使一串记录,按照其中的某个或者某些关键字的大小,递增或递减的排列起来的操作

稳定性: 假定在排序序列中,存在多个具有相同的关键字记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,存在r[i] = r[j],且r[i]在 r[j] 之前，而在排序后的序列中,r[i] 仍在 r[j]之前,则称这种算法排序为稳定的,否则称为不稳定。

内部排序: 数据元素全部放在内存中的排序

外部排序: 数据元素太多,不能同时放在内存中, 根据排序过程中的要求不能再内外存之间移动数据的排序。

插入排序

把待排序的记录按其关键码值的大小逐个插入到一个已经排好的序列中,直到所有的记录插入完为止,得到一个新的有序队列.我们生活中在玩扑克的时候,就用到了直接插入排序的思想。

直接插入排序

代码实现

一张图带你看懂内层循环

看完了代码接下来我们分析一下时间复杂度.在最坏的情况下,每插入一个数据,就要执行j次,那么时间复杂度就为(1+ 2 + 3+...+n) = O（n^2） 。最好的情况下：当我们待插入的数据本来就有序的时候，时间复杂度为O(N)。我们会发现：当元素集合越接近有序，直接插入排序的时间效率越高。

当数据基本有序的时候建议采用直接插入排序。

直接插入排序的空间复杂度O(1).是一种稳定的排序算法。

希尔排序(缩小增量排序）

希尔排序的基本思想是：先须选定一个整数，把待排序文件中所有记录分成多个组，所有距离相同的分在同一个组，并对每一个组内的记录进行排序，然后，重复上述分组和排序的工作，当达到 = 1时，所有记录在同一个组内并排好序。

图形展示

希尔排序是一种特殊的直接插入排序，直接插入排序的时间复杂度为O(N^2),在希尔排序中,分的组数越多,每组的数据就越少,O(N^2)也很小,在继续分组的时候,数据就会趋近与有序,组数少,数据多,当gap = 1时,就相当于直接插入排序。

代码实现

希尔排序的总结:

1 希尔排序是对直接插入排序的优化

2 当 gap > 1时,都是预排序,目的是让数组趋近于有序,当gap == 1时,数组已经趋近有序,这样就会很快.对整体而言,可以达到优化的效果

3 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难计算.导致好多书中给出的希尔排序时间复杂度都不固定

选择排序

思想:  每一次从待排序序列的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完.

动图演示 :

直接选择排序

直接选择排序的特性总结

1  直接选择排序的效率不是很高(不论数组中的数据是否有序,都会执行完所有步骤)

2  时间复杂度  O(N^2)

3  空间复杂度  O(1)

4 稳定性:不稳定

根据上面代码,我们想想还有没有其其它的思路, 我们可以在一次遍历中找到最大值和最小值,定义left = 0 ;rigtht = array.length - 1 ,每遍历一次,让最小值交换到left的位置,让最大值交换到right为止.但 当最大值的位置等于left的时候,在这里面有一个小小的bug.

这种方法虽然一次可以交换两个数,但时间复杂度没变,还是O(N^2).

堆排序

关于堆的性质和如何创建大跟堆,小根堆请看我的另外一篇博客,那里面有很详细的讲解

堆的基本操作和堆的创建方法

堆排序的动图演示

堆排序的代码还是比较复杂的,需要对堆的一些性质和堆的创建方法有一定的了解

public void heapSort(int[] array) {
        createBigHeap(array);
        int end = array.length - 1;
        while(end > 0) {
            swap(array,0,end);
            shiftDown(array,0,end);;
            end--;
        }
        
    }
    //建大根堆
    private void createBigHeap(int[] array) {
        for(int parent = (array.length - 1- 1)/2; parent >= 0; parent--) {
            shiftDown(array,parent,array.length);
        }
    }
    //向下tiaoz
    private void shiftDown(int[] array,int parent,int len) {
        int child = 2*parent + 1;
        while(child < len) {
            if(child + 1 < len && array[child] < array[child+1]) {
                child++;
            }
            if(array[child] > array[parent])  {
                swap(array,child,parent);
                parent = child;
                child = 2*parent + 1;
            }
            else {
                break;
            }
        }
    }
    //交换
    private void swap(int[] array,int i,int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

堆排序的特性总结 

堆排序的时间复杂度 O(N * log₂ N)

空间复杂度:  O(1)

稳定性:  不稳定的排序.

交换排序

交换排序就是根据序列中两个元素的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将元素较大的的记录向序列的尾巴移动,较小元素向序列的前面移动

冒泡排序

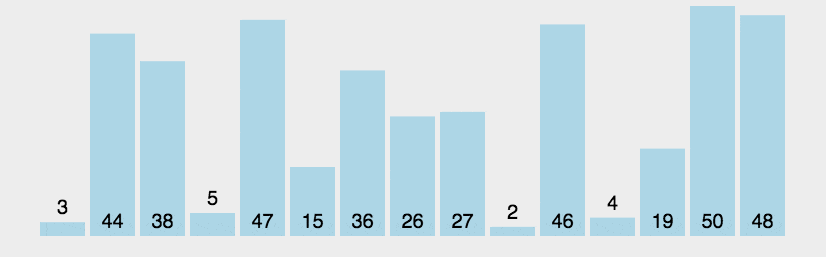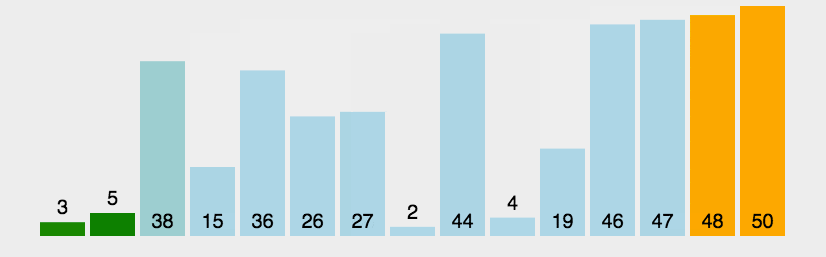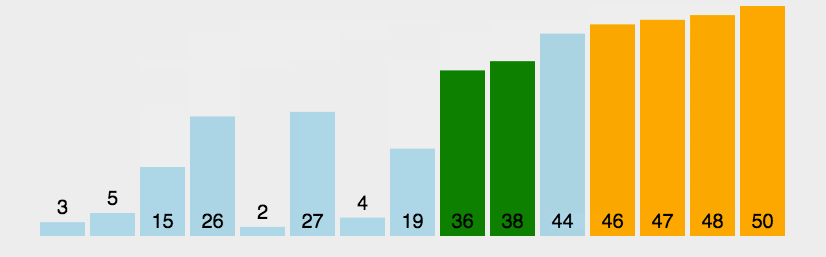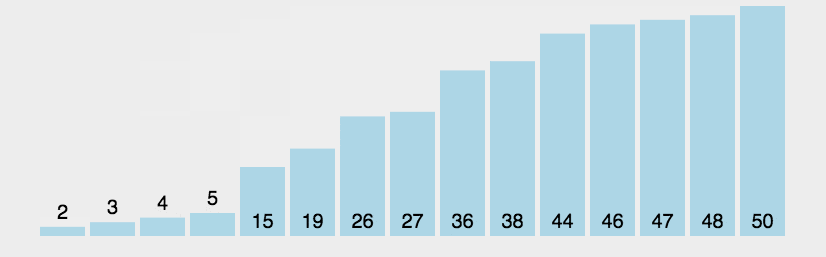
根据动图我们可以看出每遍历一次,至少有一个元素的序列是排好了的,,我么可以引入一个布尔变量flag,用来标记相邻元素是否交换,若在一次遍历中,flag的值没变,说明这组序列已经排好序.

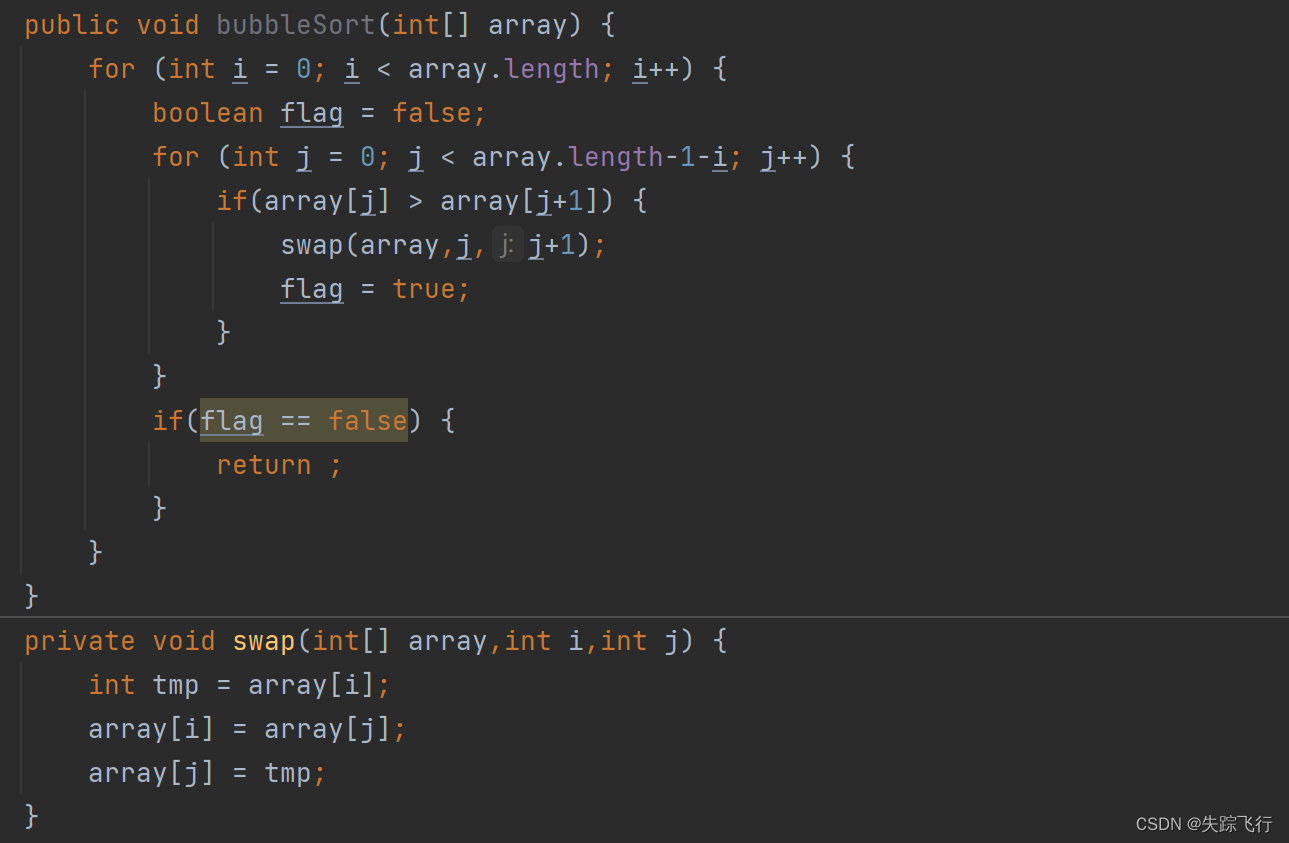
冒泡排序的特性总结

时间复杂度: O(N^2)

空间复杂度: O(1)

稳定性 : 稳定的排序