• 知识储备--基础算法篇-二叉树

    1.二叉树理论

    1.1二叉树的种类

    1. 满二叉树：所有节点的数目等于2**k-1
    2. 完全二叉树：除了底层之外其他层都是满的，最底层的节点是从左到右连续的。
    3. 二叉搜索树：左边子树的所有节点都小于中间节点，右边子树的所有节点都大于中间节点。并且左子树也是满足这个规律的。搜索数的时间复杂度为logN。
    4. 平衡二叉搜索树：左子树和右子树的深度差不能超过1。且左子树也符合这个规则。

    1.2存储方式

    1. 链式存储：每个节点包括val和左右指针指向左右节点。
    2. 顺序存储：用一个数组来存储，数组中的值是二叉树的节点值，索引是从上到下，从左到右的顺序。比如：给你一个索引i，下标为i的节点的左子节点下标是2*i+1，右子节点下标是2*i+2。

    1.3遍历方式

    1. 深度优先搜索：深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索树和图数据结构的算法。它从起始节点开始，沿着一条路径尽可能深入地探索，直到无法继续为止，然后回溯并尝试其他路径。DFS通常使用递归或栈数据结构来实现。前中后序遍历都是深度优先搜索。一般是递归法和迭代法。
    2. 广度优先搜索：广度优先搜索（Breadth-First Search，BFS）是一种用于遍历或搜索树和图数据结构的算法。与深度优先搜索不同，BFS从起始节点开始，首先探索其所有相邻节点，然后再逐层向外扩展。这意味着它会先访问离起始节点最近的节点，然后依次访问距离更远的节点。层序遍历是广度优先搜索。一般是迭代法。用队列（先进先出）来进行。

    前序遍历的顺序是：中左右。

    中序遍历是：左中右。

    后序遍历是：左右中。 

    其实表示的就是中在其中所处的位置。

    2.算法题

    2.1第94题-二叉树的中序遍历

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def inorderTraversal(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: List[int]
    12.         """
    13.         # 中序遍历是左中右
    14.         # 这是深度优先搜索dfs
    15.         # 一般是递归法和迭代法
    16.         def dfs(cur, value):
    17.             if cur == None:
    18.                 return
    19.             
    20.             dfs(cur.left, value)
    21.             value.append(cur.val)
    22.             dfs(cur.right, value)
    23.         
    24.         value = []
    25.         dfs(root, value)
    26.         return value

    递归比较简单，主要还是要掌握迭代的做法。 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def inorderTraversal(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: List[int]
    12.         """
    13.         # 中序遍历是左中右
    14.         # 这是深度优先搜索dfs
    15.         # 一般是递归法和迭代法
    16.         # 用迭代法
    17.         # 栈，用来储存节点地址
    18.         stack = []
    19.         # 用来储存结果
    20.         res = []
    21.         while root or stack:
    22.             # 先把左节点一直走到底
    23.             if root:
    24.                 stack.append(root)
    25.                 root = root.left
    26.             # 如果左节点都放入栈中了
    27.             else:
    28.                 # 弹出栈中最上面的节点
    29.                 temp = stack.pop()
    30.                 # 储存该节点的值
    31.                 res.append(temp.val)
    32.                 # 将该节点的右子节点作为根节点遍历，如果没有右节点这个就是左，再次弹出最上面的节点，储存值，这个值是中，再以该节点的右子节点作为根节点，这个值是右。
    33.                 root = temp.right
    34.             
    35.         return res

    2.2第104题-二叉树的最大深度

    心得：不知道为什么使max_deepth为数值的时候，输出的总是初始值，明明在函数里变化了的。最后只好改成了数组，输出数组最后的值。 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def maxDepth(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: int
    12.         """
    13.         # 遍历二叉树，用深度优先搜索的方式
    14.         # 就用前序遍历吧，顺序是中左右
    15.         # 先用递归法，后用迭代法
    16.         
    17.         def dfs(root, deepth, max_deepth):
    18.             if not root:
    19.                 return
    20.             deepth += 1
    21.             if max_deepth[-1] < deepth:
    22.                 max_deepth.append(deepth)
    23.             dfs(root.left, deepth, max_deepth)
    24.             dfs(root.right, deepth, max_deepth)
    25.             deepth -= 1
    26.  
    27.         deepth = 0
    28.         max_deepth = [0]
    29.         dfs(root, deepth, max_deepth)
    30.  
    31.         return max_deepth[-1]

    心得：二叉树是一个天然的递归，算最大深度只需要算每个小树的深度，也就是左树深度+右树深度+1，不断递归得到。 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def maxDepth(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: int
    12.         """
    13.         # 遍历二叉树，用深度优先搜索的方式
    14.         # 就用前序遍历吧，顺序是中左右
    15.         # 先用递归法，后用迭代法
    16.         # 用栈
    17.         if root == None:
    18.             return 0
    19.         left = self.maxDepth(root.left)
    20.         right = self.maxDepth(root.right)
    21.         deepth = max(left,right)
    22.  
    23.         return deepth+1

    2.3第226题-翻转二叉树

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def invertTree(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: TreeNode
    12.         """
    13.         steam = root
    14.         def invert(root):
    15.             if root == None:
    16.                 return
    17.             # 翻转大树，小树也要翻转，一眼递归
    18.             temp = root.left
    19.             root.left = root.right
    20.             root.right = temp
    21.             invert(root.left)
    22.             invert(root.right)
    23.  
    24.         invert(root)
    25.         
    26.         return steam

    2.4第101题-对称二叉树

    给你一个二叉树的根节点 root ， 检查它是否轴对称。

    示例 1：

    心得：自己能想到怎么做，但是代码不知道怎么写，解析是定义了一个新函数来判断。应该思考到如果轴对称需要满足几个条件，两个指针分别指向左右子树，两个指针的val值相等，并且左指针的左子树等于右指针的右子树。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def isSymmetric(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: bool
    12.         """
    13.         # 递归，左右同时开始，结构一样就继续往下，不一样就返回false
    14.         # 层遍历
    15.         # 或者分成左右两个树，每一步都同时往下深度优先搜索
    16.         return self.check(root, root)
    17.  
    18.     def check(self, p, q):
    19.         if p==None and q==None:
    20.             return True
    21.         if p==None or q==None:
    22.             return False
    23.         return p.val==q.val and self.check(p.left, q.right) and self.check(p.right, q.left)

    下面的方法更容易理解 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def isSymmetric(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: bool
    12.         """
    13.         # 递归，左右同时开始，结构一样就继续往下，不一样就返回false
    14.         # 层遍历
    15.         # 或者分成左右两个树，每一步都同时往下深度优先搜索
    16.         if not root:
    17. 			return True
    18.         def dfs(left,right):
    19.             # 递归的终止条件是两个节点都为空
    20. 			if not (left or right):
    21. 				return True
    22.             # 或者两个节点中有一个为空
    23. 			if not (left and right):
    24. 				return False
    25.             # 或者两个节点的值不相等
    26. 			if left.val!=right.val:
    27. 				return False
    28. 			return dfs(left.left,right.right) and dfs(left.right,right.left)
    29. 		# 用递归函数，比较左节点，右节点
    30.         return dfs(root.left,root.right)

    用队列做

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def isSymmetric(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: bool
    12.         """
    13.         # 队列实现
    14.         queue = [root.left, root.right]
    15.         while queue:
    16.             # pop(0)是从头弹出，pop()是从尾弹出
    17.             left = queue.pop(0)
    18.             right = queue.pop(0)
    19.             # 如果都是None,继续循环
    20.             if not (left or right):
    21.                 continue
    22.             # 如果其中一个是None
    23.             if not (left and right):
    24.                 return False
    25.             if left.val != right.val:
    26.                 return False
    27.             queue.append(left.left)
    28.             queue.append(right.right)
    29.             queue.append(left.right)
    30.             queue.append(right.left)
    31.         return True

    2.5第543题-二叉树的直径

    给你一棵二叉树的根节点，返回该树的 直径 。

    二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

    两节点之间路径的 长度 由它们之间边数表示。

    示例 1：

    输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

    心得：想到了怎么来求，但就是不会写。 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def diameterOfBinaryTree(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: int
    12.         """
    13.         if root.left==None and root.right==None:
    14.             return 0
    15.         # 左右两边可以分开算
    16.         # 直径等于左子树直径加右子树直径
    17.         # 选出最大的
    18.         # 父节点的直径等于左右子树中最大直径的边相加
    19.         self.max_depth = 1
    20.         def depth(node):
    21.             if node == None:
    22.                 return 0
    23.             L = depth(node.left)
    24.             R = depth(node.right)
    25.             deep = L + R
    26.             self.max_depth = max(deep, self.max_depth)
    27.             
    28.             return max(L, R) + 1
    29.         
    30.         depth(root)
    31.  
    32.         return self.max_depth

    2.6第102题- 二叉树的层序遍历

    心得：二叉树必须要熟练掌握BFS和DFS，几乎所有题都会用到，DFS主要就是递归，BFS主要就是队列维护节点。不断弹出和入队。 

    第一个有问题的地方就是数组需要==[]，而不是None。

    第二个地方是store数组需要及时清零。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def levelOrder(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: List[List[int]]
    12.         """
    13.         if root == None:
    14.             return []
    15.         # 层序遍历用迭代,迭代用栈或队列
    16.         # 广度优先搜索, BFS加一个层序
    17.         result = []
    18.         queue = []
    19.         queue.append(root)
    20.         store = []
    21.         temp2 = []
    22.         while queue != []:
    23.             temp = queue.pop(0)
    24.             store.append(temp.val)
    25.             if temp.left != None:
    26.                 temp2.append(temp.left)
    27.             if temp.right != None:
    28.                 temp2.append(temp.right)
    29.             if queue == []:
    30.                 result.append(store)
    31.                 store = []
    32.                 queue = temp2
    33.                 temp2 = []
    34.         return result

    2.7第108题-将有序数组转化为二叉搜索树

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def sortedArrayToBST(self, nums):
    9.         """
    10.         :type nums: List[int]
    11.         :rtype: TreeNode
    12.         """
    13.         # 递归
    14.         length = len(nums)
    15.         if length == 1:
    16.             return TreeNode(nums[0])
    17.         self.steam = None
    18.         def dfs(nums):
    19.             length = len(nums)
    20.             if length == 1:
    21.                 return TreeNode(nums[0])
    22.             mid = nums[length/2]
    23.             left = nums[:length/2]
    24.             L = dfs(left)
    25.             R = None
    26.             if length/2+1 < length:
    27.                 right = nums[length/2+1:]
    28.                 R = dfs(right)
    29.             self.steam = TreeNode(mid, L, R)
    30.             return self.steam
    31.  
    32.         dfs(nums)
    33.  
    34.         return self.steam

    2.8第98题-验证二叉搜索树

    心得：方法还是很容易想到的，至于遍历方法有递归、迭代、队列，需要自己想一下哪种合适，然后写出每种方法对应的基础框架，在上面进行修改，带入到最左下角的节点，主要考虑终止条件、需要左右子树返回的值，result的填入顺序。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def isValidBST(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: bool
    12.         """
    13.         # 遍历二叉树，从最左下的点开始遍历，最后数组是绝对升序的
    14.         # 用dfs试试
    15.         result = []
    16.         def dfs(root):
    17.             if root == None:
    18.                 return
    19.             dfs(root.left)
    20.             result.append(root.val)
    21.             dfs(root.right)
    22.             return
    23.         
    24.         dfs(root)
    25.         for i in range(1,len(result)):
    26.             if result[i-1] < result[i]:
    27.                 continue
    28.             else:
    29.                 return False
    30.         
    31.         return True

    心得：看了解析，直接递归，每个子树判断一下是否大于下限小于上限即可，并且上下限是实时更新的。这种返回True和False的题最好把递归放到return里面，这样一旦有一个false就能马上弹出递归，很方便。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def isValidBST(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: bool
    12.         """
    13.         # 遍历二叉树，从最左下的点开始遍历，最后数组是绝对升序的
    14.         # 用dfs试试
    15.         flag = True
    16.         def helper(root, upper = float('inf'), lower = float('-inf')):
    17.             if root == None:
    18.                 return True
    19.             if not (root.val < upper and root.val > lower):
    20.                 return False
    21.             return helper(root.left, upper=root.val, lower=lower) and helper(root.right, upper=upper, lower=root.val)
    22.         
    23.         flag = helper(root)
    24.  
    25.         return flag

    2.9第230题-二叉搜索树中第k小元素

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def kthSmallest(self, root, k):
    9.         """
    10.         :type root: TreeNode
    11.         :type k: int
    12.         :rtype: int
    13.         """
    14.         # 首先想到的肯定是遍历打印，然后选出第k个，但是那样效率太低
    15.         # 先找到最小的值，然后慢慢返回查找第k个，中序遍历
    16.         num = 0
    17.         self.result = 0
    18.         def dfs(root, num):
    19.             if root == None:
    20.                 return num
    21.             if num == k:
    22.                 self.result = root.val
    23.                 return num + 1
    24.             temp = dfs(root.left, num)
    25.             if temp == k:
    26.                 return k
    27.             num = temp + 1
    28.             if num == k:
    29.                 self.result = root.val
    30.                 return num + 1
    31.             temp = dfs(root.right, num)
    32.             if temp == k:
    33.                 return k
    34.  
    35.             return temp
    36.  
    37.         dfs(root, num)
    38.  
    39.         return self.result

    用迭代法节省时间，遇到了等于k的就可以结束程序。要熟练掌握迭代法前中后序遍历。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def kthSmallest(self, root, k):
    9.         """
    10.         :type root: TreeNode
    11.         :type k: int
    12.         :rtype: int
    13.         """
    14.         # 首先想到的肯定是遍历打印，然后选出第k个，但是那样效率太低
    15.         # 先找到最小的值，然后慢慢返回查找第k个，中序遍历
    16.         # 用迭代的方法可以不用遍历整个二叉树
    17.         stack = []
    18.         target = 0
    19.         result = 0
    20.         while root or stack:
    21.             if root:
    22.                 stack.append(root)
    23.                 root = root.left
    24.             else:
    25.                 temp = stack.pop()
    26.                 target += 1
    27.                 if target == k:
    28.                     result = temp.val
    29.                     break
    30.                 root = temp.right
    31.         
    32.         return result

    2.10第199题-二叉树的右视图

    可以用BFS，层序遍历，从左到右遍历存储每层最后一个节点，也可以从右到左，存储每层第一个节点。

    可以用DFS，从右开始向下遍历，记录深度，从左子树的时候超过深度就添加到结果中。

    两种方法都想到了，但是DFS没写出来，BFS相对简单，写出来了。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def rightSideView(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: List[int]
    12.         """
    13.         # 相当于先从右走，如果右不存在再从左走
    14.         # 如果右子树走到头了，左子树比右子树深
    15.         # 则再从左往下走，所以两颗子树应该同时走
    16.         # 层遍历，只保存最右边的
    17.         if root == None:
    18.             return None
    19.         result = []
    20.         result.append(root.val)
    21.         queue = []
    22.         queue.append(root)
    23.         temp2 = []
    24.         store = []
    25.         while queue != []:
    26.             temp = queue.pop(0)
    27.             if temp.right:
    28.                 temp2.append(temp.right)
    29.             if temp.left:
    30.                 temp2.append(temp.left)
    31.             if queue == []:
    32.                 if temp2 != []:
    33.                     result.append(temp2[0].val)
    34.                 queue = temp2
    35.                 temp2 = []
    36.                 
    37.         return result

    2.11第114题-二叉树展开为链表

    给你二叉树的根结点 root ，请你将它展开为一个单链表：

    • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
    • 展开后的单链表应该与二叉树 先序遍历 顺序相同。

    示例 1：

    输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

    心得：太蠢了，应该想到的，一直想不到怎么使5接到4后面，只需要用前序遍历，维护好子树返回上来的地址就行了。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def flatten(self, root):
    9.         """
    10.         :type root: TreeNode
    11.         :rtype: None Do not return anything, modify root in-place instead.
    12.         """
    13.         # 前序遍历
    14.         # DFS，递归或者迭代
    15.         def dfs(root, result):
    16.             if not root:
    17.                 return None
    18.             result.append(root)
    19.             dfs(root.left, result)
    20.             dfs(root.right, result)
    21.             
    22.         result = []
    23.         dfs(root, result)
    24.         for i in range(len(result)-1):
    25.             result[i].right = result[i+1]
    26.             result[i].left = None
    27.  
    28.         return root

    2.12从前序与中序遍历序列构造二叉树

    给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

    示例 1:

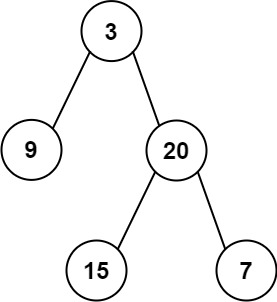
    输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

    心得：递归！！ 

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def buildTree(self, preorder, inorder):
    9.         """
    10.         :type preorder: List[int]
    11.         :type inorder: List[int]
    12.         :rtype: TreeNode
    13.         """
    14.         # 前序遍历中，第一个数一定是根节点
    15.         # 中序遍历中，根节点对应val左边的数就是左子树，右边的是右子树
    16.         # 递归
    17.         def dfs(preorder, inorder):
    18.             if len(preorder) == 0:
    19.                 return None
    20.             num = preorder.pop(0)
    21.             root = TreeNode(num)
    22.             ind = inorder.index(num)
    23.             left = inorder[:ind]
    24.             right = inorder[ind+1:]
    25.             root.left = dfs(preorder[:len(left)], left)
    26.             root.right = dfs(preorder[len(left):], right)
    27.  
    28.             return root
    29.             
    30.         return dfs(preorder, inorder)

    2.13第437题-路径总和|||

    给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

    路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

    示例 1：

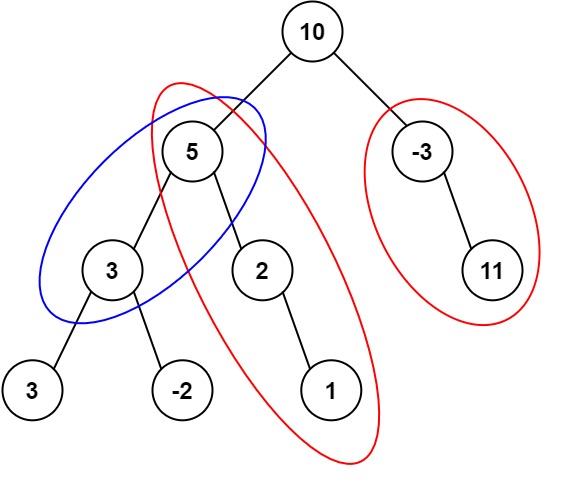
    输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

    心得：想用一个数组把每个往下的路径的点存起来，遍历得出有多少条，试一下，果然超时。

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, val=0, left=None, right=None):
    4. #         self.val = val
    5. #         self.left = left
    6. #         self.right = right
    7. class Solution(object):
    8.     def pathSum(self, root, targetSum):
    9.         """
    10.         :type root: TreeNode
    11.         :type targetSum: int
    12.         :rtype: int
    13.         """
    14.         # dfs前序遍历
    15.         self.count = 0
    16.         self.depth = 0
    17.         def dfs(root, store):
    18.             if not root:
    19.                 return None
    20.             self.depth += 1
    21.             deep = self.depth
    22.             store.append(root.val)
    23.             num = 0
    24.             
    25.             for i in range(len(store)):
    26.                 for j in range(i,len(store)):
    27.                     num += store[j]
    28.                 if num == targetSum:
    29.                     self.count += 1
    30.                 num = 0
    31.             temp = dfs(root.left, store)
    32.             if temp:
    33.                 store = store[:deep]
    34.             dfs(root.right, store)
    35.             self.depth = deep-1
    36.  
    37.             return root
    38.         
    39.         store = []
    40.         dfs(root, store)
    41.  
    42.         return self.count

    2.14第236题-二叉树的最近公共祖先

    暴力存储

    1. # Definition for a binary tree node.
    2. # class TreeNode(object):
    3. #     def __init__(self, x):
    4. #         self.val = x
    5. #         self.left = None
    6. #         self.right = None
    7.  
    8. class Solution(object):
    9.     def lowestCommonAncestor(self, root, p, q):
    10.         """
    11.         :type root: TreeNode
    12.         :type p: TreeNode
    13.         :type q: TreeNode
    14.         :rtype: TreeNode
    15.         """
    16.         # DFS, 用栈的方式迭代
    17.         stack = []
    18.         stack.append(root)
    19.         store = []
    20.         store2 = []
    21.         store3 = []
    22.         depth = 0
    23.         while stack or root:
    24.             if store == [] or store2 == []:
    25.                 if root:
    26.                     stack.append(root)
    27.                     stack.append(root)
    28.                     if root == p:
    29.                         store = copy.deepcopy(stack)
    30.                     if root == q:
    31.                         store2 = copy.deepcopy(stack)
    32.                     
    33.                     root = root.left
    34.                 else:
    35.                     temp = stack.pop()
    36.                     root = temp.right
    37.             else:
    38.                 break
    39.  
    40.         a = len(store)
    41.         b = len(store2)
    42.         for i in reversed(range(a)):
    43.             for j in reversed(range(b)):
    44.                 if store[i].val == store2[j].val:
    45.                     return store[i]

     

  • 相关阅读:
    通信用多模光纤主要有哪些类型？OM1～OM5有什么区别
    python---类与对象
    dependencies和devDependencies的区别
    【Python基础】Python十进制二进制八进制十六进制 ascii转换
    《动机与人格》笔记(一)——人类似乎从来就没有长久地感到过心满意足
    C++校园导游程序及通信线路设计
    泡泡玛特：一家中国潮玩品牌的出海之旅
    阿里为何禁止在对象中使用基本数据类型
    el-table 列分页
    电脑便签功能在哪里找？电脑桌面便签怎么添加？
  • 原文地址：https://blog.csdn.net/Orange_sparkle/article/details/132939792