-
矩阵论—线性子空间、生成子空间、核空间、零度、子空间的交与和、直和
线性子空间定义

如果
 ,V1称为平凡子空间,否则称为非平凡子空间。
,V1称为平凡子空间,否则称为非平凡子空间。生成子空间


核空间、零度


解:
rank(A)=2; n(A)=N-rank(A)=3-2=1,这里N表示的是未知量的个数。
n(A)也可以理解为基础解系的个数,即基础解系中有几个向量。结论:
(1)rnak(A) + n(A) = A 的列数
(2)n(A) - n(A^T) = (A的列数) -(A的行数)子空间的交与和





例题:


直和




综合例题:


解:

 再例如:
再例如:

再例如:


再求两个子空间交的维数:
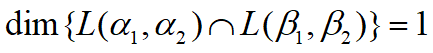
-
相关阅读:
si446使用记录(一):基本资料获取
JAVASE事件监听
电子签名组件Vue
java基于Springboot+vue 音乐播放器论坛交流管理系统 element 前后端分离
Flutter:环境搭建、项目创建
R 和 Python用于统计学分析,哪个更好?
matlab和python做zscore结果不一样的问题
什么是灰度发布?能给技术开发带来什么价值
【Nginx】Nginx 鉴权 (htpasswd) + Nginx 文件下载配置
windows安装linux部署docker服务全过程
- 原文地址:https://blog.csdn.net/m0_48241022/article/details/132782972