算法 数据结构 斐波那契数列 递归实现斐波那契数列 斐波那契递归的优化 斐波那契数列递归求解 多路递归实现 斐波那契算法系列 数据结构（十一）

1. 什么是斐波那契数列：

• 之前的例子是每个递归函数只包含一个自身的调用，这称之为 single recursion

• 如果每个递归函数例包含多个自身调用，称之为 multi recursion

递推关系

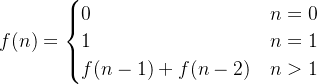
下面的表格列出了数列的前几项

多路递归斐波那契代码实现1：

package com.nami.algorithm.study.day07;
 
/**
 * beyond u self and trust u self.
 *
 * @Author: lbc
 * @Date: 2023-09-06 9:29
 * @email: 594599620@qq.com
 * @Description: keep coding
 */
public class Fibonacci {
 
    /**
     * 出现问题的，计算 n= 88 根本算不出来。多路递归一直在循环里面了。出不来 --！
     * @param n
     * @return
     */
    public static int calculate(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        int f1 = calculate(n - 1);
        int f2 = calculate(n - 2);
        return f1 + f2;
    }
 
 
    public static void main(String[] args) {
        // 时间复杂度： 2*f(n+1) -1
        // E(1.618N次方)
        System.out.println(calculate(88));
    }
 
}

  非递归实现2 --- LeetCode 70. 爬楼梯 计算爬楼梯共计多少种方法可达_不努力就种地~的博客-CSDN博客

  之前写的爬楼梯解决方案：

public static  int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

这种方法直接用数组去存储前面计算的值，不用重复计算。没有出现上面n=88出现的计算缓慢问题

递归优化方案：

                       使用数组，存储之前计算的数据，减少计算次数。妙哉

package com.nami.algorithm.study.day07;
 
import java.util.Arrays;
 
/**
 * beyond u self and trust u self.
 *
 * @Author: lbc
 * @Date: 2023-09-06 9:29
 * @email: 594599620@qq.com
 * @Description: keep coding
 */
public class FastFibonacci {
 
    /**
     * 出现问题的，计算 n= 100000
     * 出现异常 StackOverflowError
     * 方法层级太深，会导致栈溢出
     *
     * @param n
     * @return
     */
    public static int calculate(int n) {
        // 初始化缓存
        // ==>记忆法
        // 空间换时间
        int[] cache = new int[n + 1];
 
        // 填充-1 标识未该值为计算
        Arrays.fill(cache, -1);
        cache[0] = 0;
        cache[1] = 1;
        return fibonacci(n, cache);
    }
 
    /**
     * 时间复杂度： O(n)
     * 增加额外空间成本
     *
     * @param n
     * @param cache
     * @return
     */
    private static int fibonacci(int n, int[] cache) {
        if (cache[n] != -1) {
            return cache[n];
        }
        int f1 = fibonacci(n - 1, cache);
        int f2 = fibonacci(n - 2, cache);
        cache[n] = f1 + f2;
        return cache[n];
    }
 
    public static void main(String[] args) {
        // n=88也有问题，出现-值
        // -2092787285
        System.out.println(calculate(88));
    }
 
}

使用数组进行优化，也有一个问题，数组只有n-1, n-2两个值有用。对于计算之后，存储前面n-3的值没有了意义；
 

优化2 ==>尾递归:

                            尾递归（防止栈溢出） +  只取n-1, n-2的值流转

package com.nami.algorithm.study.day07;
 
/**
 * 尾递归 斐波那契数列
 * beyond u self and trust u self.
 *
 * @Author: lbc
 * @Date: 2023-09-06 9:29
 * @email: 594599620@qq.com
 * @Description: keep coding
 */
public class TailRecFibonacci {
 
    /**
     * @param n
     * @return
     */
    public static int calculate(int n) {
        return fibonacci(n, 0, 1);
    }
 
    private static int fibonacci(int n, int first, int second) {
        if (n == 0) {
            return first;
        }
        if (n == 1) {
            return second;
        }
        return fibonacci(n - 1, second, first + second);
    }
 
    public static void main(String[] args) {
        // n=47，出现-值
        // -1323752223
        // 18 3631 1903 + 11 3490 3170
        //    n= 46     +    n=45
        // int 最大值 21 4748 3647
        System.out.println(calculate(46));
    }
 
}

为什么斐波那契数列会出现负值？

      当n=88时，结果等于负数。排查发现：当n=46是正常的，n=47时，前面两个值的相加已经超过了int最大值int.max_value= 21 4748 3647 所以出现负数

如何根本上解决爆栈问题：

                                   递归转for or while循环解决问题。