• C++之AVL树

    AVL树

    AVL树的概念

    二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。、

    一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

    • 它的左右子树都是AVL树
    • 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

    在这里插入图片描述
    如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O(logN)，搜索时间复杂度O(logN)；

    AVL树节点的定义

    我们这儿是以KV模型来实现 AVL树，我们在实现过程中需要构建一个三叉链结构，并且还需要引入一个平衡因子：

    template<class K, class V>
struct AVLTreeNode
{
	//存储键值对
	pair<K, V> _kv;

	//三叉链结构
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;

	//平衡因子
	int _bf;

	//构造函数
	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23

    AVL树的插入

    AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

    1. 按照二叉搜索树的方式插入新节点；
    2. 调整节点的平衡因子，如果出现不平衡，就进行旋转；

    首先我们需要根据二叉搜索树的规则进行插入操作，分为三步：

    1. 如果待插入值小于根结点的值，在左子树中去寻找；
    2. 如果待插入值大于根结点的值，在右子树中去寻找；
    3. 如果待插入值等于于根结点的值，返回false；

    当我们寻找到空位置以后就可以进行插入，但是插入新结点以后，就可能会出现树的高度变化的问题，此时我们的平衡因子就会随之发生改变，这时我们就需要去调整平衡因子，进而来判断树是否平衡。

    而我们更新平衡因子的规则如下：

    • 如果新插入结点在parent的左侧，parent结点的平衡因子就- -；
    • 如果新插入结点在parent的右侧，parent结点的平衡因子就++；

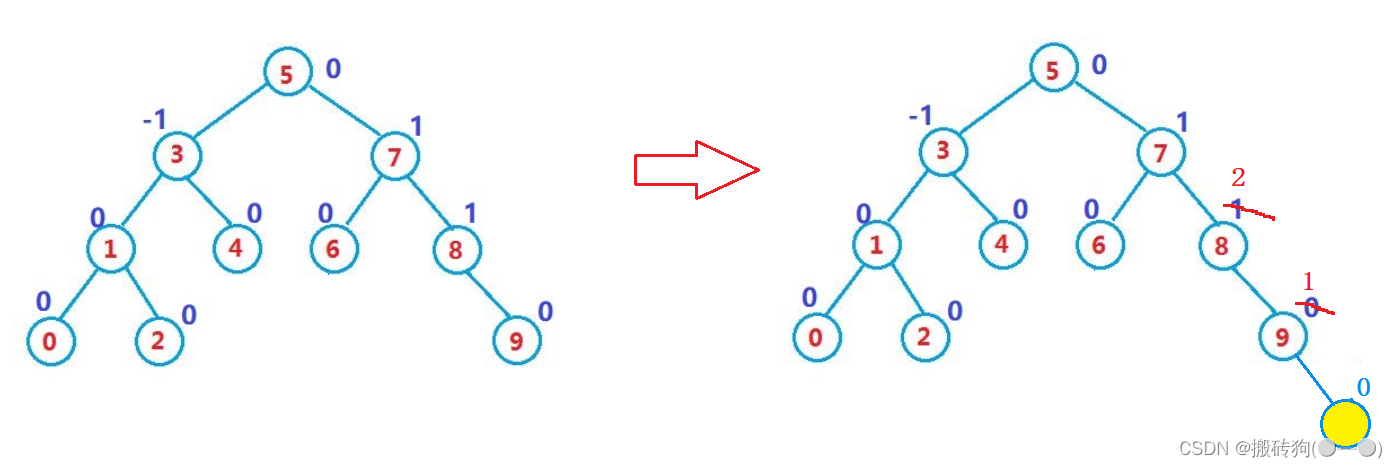
    更新平衡因子以后，我们就需要进行相应的检查，也分为三种情况：

    • 更新平衡因子以后，如果parent平衡因子变为0，说明插入以前parent结点平衡因子为1 or -1，此时插入结点位置就在parent较矮的那一边，插入以后parent左右子树高度相等，就不会影响整棵树的高度，就不需要往上更新了；
      在这里插入图片描述

    • 更新平衡因子以后，如果parent平衡因子变为1 or -1，说明插入以前parent结点平衡因子为0，此时插入结点位置以后就改变了树的高度，就需要继续往上更新；
      在这里插入图片描述

    • 更新平衡因子以后，如果parent平衡因子变为2 or -2，说明此时树已经不平衡了，我们就需要进行旋转操作了。
      在这里插入图片描述
      代码实现：

    template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool insert(const pair<K, V>& kv)
	{
		//如果此时根结点为空，创建结点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			//待插入值小于根结点的值，在左子树中去寻找
			if (cur->first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			//待插入值大于根结点的值，在右子树中去寻找
			else if (cur->first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			//待插入值等于于根结点的值，返回false
			else
			{
				return false;
			}
		}
		//创建待插入的结点
		cur = new Node(kv);
		//待插入的结点key值小于parent结点key值
		if (parent->_kv.first > kv.first)
		{
			//左边进行插入
			parent->_left = cur;
		}
		//待插入的结点key值大于parent结点key值
		else
		{
			//右边进行插入
			parent->_right = cur;
		}
		//被插入结点与父节点连接起来
		cur->_parent = parent;
		while (parent)
		{
			//新插入结点在左边
			if (parent->_left == cur)
			{
				//parent平衡因子--
				parent->_bf--;
			}
			//新插入结点在右边
			else
			{
				//parent平衡因子++
				parent->_kv++;
			}
			//parent平衡因子为0，不需要向上更新
			if (parent->_bf == 0)
			{
				break;
			}
			//parent平衡因子为1 or -1，需要向上更新
			else if (abs(parent->_bf) == 1)
			{
				//parent cur都想上调整
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (abs(parent->_bf) == 2)
			{
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					//左单旋
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					//右单旋
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					//左右单旋
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					//右左单旋
					RotateRL(parent);
				}
				else
				{
					assert(false);
				}
				break;
			}
			//以上情况都不是，说明插入出问题了，报错
			else
			{
				assert(false);
			}
		}
		//插入成功，返回true
		return true;
	}
private:
	Node* _root = nullptr;
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119

    AVL树的旋转

    如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

    1. parent平衡因子为2，cur平衡因子为1，进行左单旋；
    2. parent平衡因子为-2，cur平衡因子为-1，进行右单旋；
    3. parent平衡因子为-2，cur平衡因子为1，进行左右双旋；
    4. parent平衡因子为2，cur平衡因子为-1，进行右左双旋；

    左单旋

    旋转示意图如下：
    在这里插入图片描述
    左单旋的步骤就是：

    1. 让subRL作为parent的右树；
    2. 让parent作为subR的左树；
    3. 让subR作为旋转的树的根节点；
    4. 更新平衡因子。

    代码实现：

    void RotateL(Node* parent)
{
	//记录parent结点的父结点
	Node* ppNode = parent->_parent;

	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	//建立parent与subRL之间的关系
	parent->_right = subRL;
	if (subRL)
		subRL->_parent = parent;

	//建立parent与subR之间的关系
	subR->_left = parent;
	parent->_parent = subR;

	//判断根结点是否就是parent
	if (_root == parent)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (ppNode->_left == parent)
		{
			ppNode->_left = subR;
		}
		else
		{
			ppNode->_right = subR;
		}
		subR->_parent = ppNode;
	}

	//更新平衡因子
	parent->_bf = subR->_bf = 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39

    右单旋

    旋转示意图如下：
    在这里插入图片描述

    右单旋步骤如下：

    1. 让subLR作为parent的左结点；
    2. 让parent作为subL的右结点；
    3. 让subL作为旋转的这棵树的根结点；
    4. 更新平衡因子；

    代码实现：

    void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	Node* ppNode = parent->_parent;

	//建立subLR与parent关系
	parent->_left = subLR;
	if (subLR)
		subLR->_parent = parent;

	//建立subL与parent关系
	subL->_right = parent;
	parent->_parent = subL;

	//判断根结点是否就是parent
	if (_root == parent)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (ppNode->_left == parent)
		{
			ppNode->_left = subL;
		}
		else
		{
			ppNode->_right = subL;
		}
		subL->_parent = ppNode;
	}
	//更新平衡因子
	parent->_bf = subL->_bf = 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    左右双旋

    b，c新增结点都会导致左右双旋情况发生，我们以b新增结点为例：
    在这里插入图片描述
    左右双旋步骤如下：

    1. 以subL为旋转点进行左单旋；
    2. 以subLR为旋转点进行右单旋；
    3. 更新平衡因子。

    左右双旋实际上就是让subLR的左右子树，分别成为subL的右子树和parent的左子树，再让subL和parent分别成为subLR左子树和右子树，最后让subLR成为根结点；

    左右双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：

    1. subLR的平衡因子是-1时，左右双旋后得到的parent，subL，subLR平衡因子分别是：1，0，0；
      在这里插入图片描述
    2. subLR的平衡因子是1时，左右双旋后得到的parent，subL，subLR平衡因子分别是：0，-1，0；
      在这里插入图片描述
    3. subLR的平衡因子是0时，左右双旋后得到的parent，subL，subLR平衡因子分别是：0，0，0；
      在这里插入图片描述
    void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	int bf = subLR->_bf;

	//以subL为旋转点进行左单旋
	RotateL(parent->_left);

	//以parent为旋转点进行右单旋
	RotateR(parent);

	//subLR平衡因子最后肯定是0
	subLR->_bf = 0;

	//更新平衡因子
	if (bf == -1)
	{
		parent->_bf = 1;
		subL->_bf = 0;
	}
	else if (bf == 0)
	{
		parent->_bf = 0;
		subL->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = 0;
		subL->_bf = -1;
	}
	else
	{
		assert(false);
	}
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    右左双旋

    b，c新增结点都会导致左右双旋情况发生，我们以c新增结点为例：
    在这里插入图片描述
    右左双旋步骤如下：

    1. 以subR为旋转点进行右单旋；
    2. 以subRL为旋转点进行左单旋；
    3. 更新平衡因子。

    右左双旋实际上就是让subRL的左右子树，分别成为subR的左子树和parent的右子树，再让subR和parent分别成为subRL右子树和左子树，最后让subsubRL成为根结点；

    左右双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：

    1. subRL的平衡因子是1时，左右双旋后得到的parent，subR，subRL平衡因子分别是：-1，0，0；
      在这里插入图片描述
    2. subRL的平衡因子是-1时，左右双旋后得到的parent，subR，subRL平衡因子分别是：0，1，0；
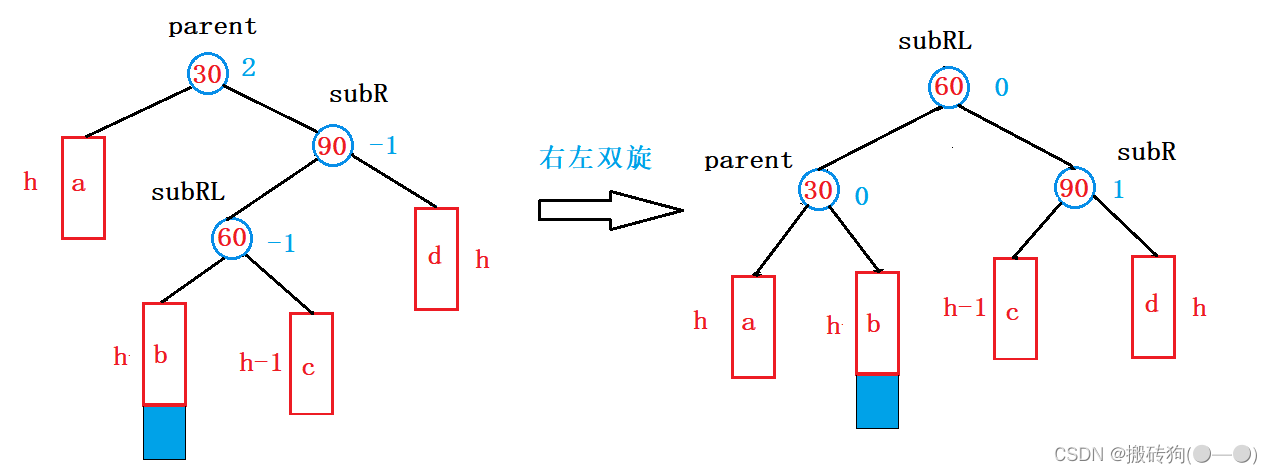
      在这里插入图片描述
    3. subRL的平衡因子是0时，左右双旋后得到的parent，subR，subRL平衡因子分别是：0，0，0；
      在这里插入图片描述
      代码实现：
    	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		int bf = subRL->_bf;

		//以subR为旋转点进行右单旋
		RotateR(parent->_right);

		//以parent为旋转点进行左单旋
		RotateL(parent);

		//subRL平衡因子最后肯定是0
		subRL->_bf = 0;

		//更新平衡因子
		if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    AVL树的验证

    AVL树是在二叉搜索树的基础上加入了平衡性的限制，也就是说AVL树也是二叉搜索树，因此我们可以先获取二叉树的中序遍历序列，来判断二叉树是否为二叉搜索树。

    我们可以使用前序遍历来打印出来进行验证：

    代码如下：

    void InOrder()
{
	_InOrder(_root);
}
	
void _InOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}

	_InOrder(root->_left);
	cout << root->_kv.first << ":" << root->_kv.second << endl;
	_InOrder(root->_right);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16

    但是前序遍历只能证明他是一个二叉搜索树，并不能证明他是一棵AVL树，我们还需要通过验证其高度是否满足AVL树的要求来证明它是否平衡，因为AVL树左右子树高度差不会超过1，我们可以通过此性质来进行验证。

    bool IsBalance()
{
	return _IsBalance(_root);
}

bool _IsBalance(Node* root)
{
	//根结点为空，是AVL树，返回真
	if (root == nullptr)
	{
		return true;
	}
	//计算左右子树高度
	int leftHT = Height(root->_left);
	int rightHT = Height(root->_right);
	//计算左右子树高度差
	int dif = rightHT - leftHT;

	if (dif != root->_bf)
	{
		cout << root->_kv.first << "平衡因子异常" << endl;
		return false;
	}
	//递归进行判断
	return abs(dif) < 2
		&& _IsBalance(root->_left)
		&& _IsBalance(root->_right);
}

int Height(Node* root)
{
	if (root == nullptr)
	{
		return 0;
	}
	return max(Height(root->_left), Height(root->_right)) + 1;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    AVL树的性能

    AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即logN。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

  • 相关阅读:
    【实践】一种基于Spring Boot最简单的RESTFul接口版本管理
    信奥中的数学：抽屉原理
    2022全球20多款知名的Android刷机ROM镜像和Android系统开源源码(覆盖全球机型)
    Java实习生常规技术面试题每日十题Java基础（五）
    chrome F12 network 保留之前请求信息
    【LeetCode:201. 数字范围按位与 | 位运算】
    NANK南卡和松下护眼台灯哪款好？最全面对比两款热门护眼台灯
    扫描器（xray和bp联动）
    默认为4G网络
    linux可视化运维工具
  • 原文地址：https://blog.csdn.net/2303_77100822/article/details/132650415