***杨辉三角_yyds_LeetCode_python***

1.题目描述：

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

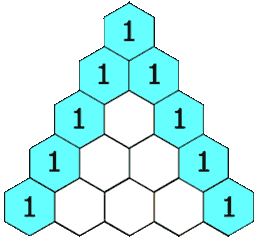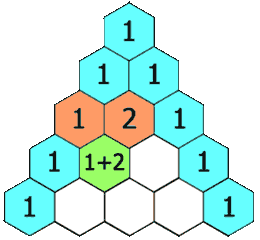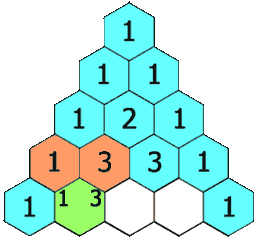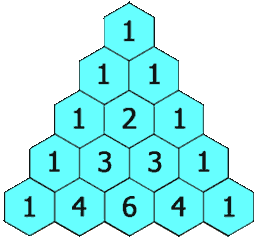
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:

输入: numRows = 1
输出: [[1]]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/pascals-triangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.题解：

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        result = [] #用来存放杨辉三角
        #
        for i in range(numRows):
            now = [1]*(i+1)
            if i >= 2:
                for  j in range(1,i):
                    now[j] = pre[j-1] + pre[j]
            result.append(now)
            pre = now
        return result
         
 
 

 

3.题目总结：

这段代码是用来生成杨辉三角的，杨辉三角是一个很有趣的数学图形，它的每一行都是由数字 1 开始和结束，中间的数字是上一行相邻两个数字之和。下面是一个 5 行的杨辉三角：

```
        1
       1 1
      1 2 1
     1 3 3 1
    1 4 6 4 1
```

现在我们来解释一下这段代码：

首先定义了一个函数 `generate`，它接收一个参数 `numRows`，表示要生成杨辉三角的行数。

然后定义了一个空列表 `result`，用来存储生成的杨辉三角。

接下来使用一个循环，循环次数为 `numRows`，也就是要生成的杨辉三角的行数。

在每次循环中，首先创建一个长度为 `i+1` 的列表 `now`，并将其初始化为 1，这个列表就是当前行的数字列表。

然后判断当前行的行数是否大于等于 2，如果是，就需要计算中间的数字。这里使用了另一个循环，循环次数为 `i-1`，也就是中间数字的个数。在循环中，将 `now` 列表中第 `j` 个数字更新为上一行相邻两个数字之和。

接下来将当前行的数字列表 `now` 添加到 `result` 列表中。

最后将当前行的数字列表 `now` 赋值给变量 `pre`，以便下一次循环使用。

最后返回 `result` 列表，即为生成的杨辉三角。