-
状态压缩dp整理
蒙德里安的梦想
求把 N × M N×M N×M 的棋盘分割成若干个 1 × 2 1×2 1×2 的长方形,有多少种方案。
例如当 N = 2 , M = 4 N=2,M=4 N=2,M=4 时,共有 5 5 5 种方案。当 N = 2 , M = 3 N=2,M=3 N=2,M=3 时,共有 3 3 3 种方案。
如下图所示:

输入格式
输入包含多组测试用例。每组测试用例占一行,包含两个整数 N 和 M N 和 M N和M。
当输入用例 N = 0 , M = 0 N=0,M=0 N=0,M=0 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。数据范围
1 ≤ N , M ≤ 11 1≤N,M≤11 1≤N,M≤11
输入样例:
1 2 1 3 1 4 2 2 2 3 2 4 2 11 4 11 0 0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
输出样例:
1 0 1 2 3 5 144 51205- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
详细解释
这题最最核心的一点是要想到:横着摆放方块的方案数 = 总摆放方块方案数。
由于 1 × 2 1×2 1×2的方块可以横着或是竖着放,观察图给样例,如果把所有能横着放的方块都放入后,竖着放的方块位置也就固定了,只管往里塞,于是结论就是要找总方案数只需要找到可以横着摆放方块的方案数。
状态表示
f[i][j]:前i - 1列的摆放状态已处理好的前提下,在i - 1列横放的小方块伸到第i列的格子状态为j的方案数。
其中j由于是一个状态表示,所以要把它想成一个二进制数,它的范围是由 n n n(一列有 n n n行)决定的,即为了表示 n n n个格子需要有 2 n 2^n 2n 个状态,即 j ∈ ( 0 , 1 < < n ) j∈(0,1 << n) j∈(0,1<<n)。
格子的摆放引起状态
这个状态定义有点长,什么意思呢?以下图为例:
表示当 i = 2 ( i 从 0 开 始 ) i=2(i从0开始) i=2(i从0开始), j = ( 11001 ) 2 j = (11001)_2 j=(11001)2时的状态, j j j中为 1 1 1的地方表示该列的这个位置被占了。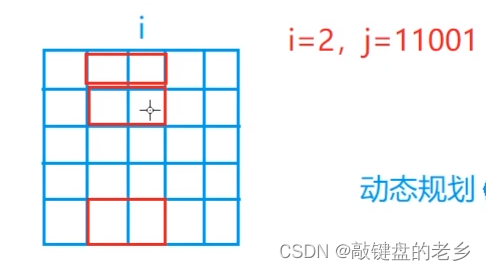
其中尤其要注意的是:第 i i i列的 j j j这个状态本质上是由于第 i − 1 i-1 i−1列状态造成影响的,也就是说, j j j中为1的地方在 i − 1 i-1 i−1列的对应位置上是横放了方块之后捅到第 i i i 列去的。
以此类推,如果定义 i − 1 i-1 i−1列上的状态是 k k k,那么这个 k k k是经过 i − 2 i-2 i−2列的方块放置影响到的,就像下图:
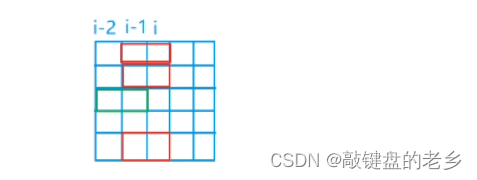
那么绿色的方块是在 i − 2 i-2 i−2列放置导致的,此时的 k = ( 00100 ) 2 k=(00100)_2 k=(00100)2,注意 ≠ 11101 ≠11101 =11101。
状态计算
由于动态规划是按列数从小到大( 0 到 m − 1 0到m-1 0到m−1)挨着枚举状态,因此第 i i i 列的方案数
f[i][j],由前一列的方案数f[i - 1][k]转移而来,即f[i][j] = Σ(f[i - 1][k])。
判断合法状态
很明显不是所有格子摆放状态都是合法的。
- 每一列的状态中连续空着的格子数不能为奇数,因为空格是给竖着放的方块留着的,方块尺寸
1
×
2
1×2
1×2,当要竖着放时遇到奇数空格注定是要么放不满要么放不下。用一个
st[]数组存,如果状态 j j j 连续空着的格子数为偶数 则st[j] = true。而状态转移时是要判断方块从 i − 2 i - 2 i−2列合在第 i − 1 i - 1 i−1列的方块共有多少个,可以“或”运算,即判断st[j | k]。 i - 2列伸到i - 1列的小方格 和i - 1列放置的小方格不能重复,啥意思呢?看下图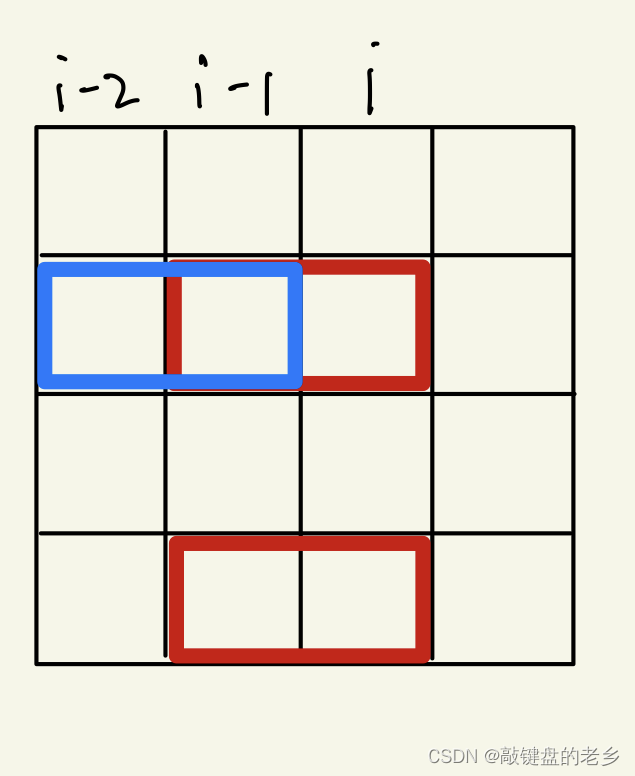
可以看到,此时蓝色的方块和红色的方块 “撞” 在了一起,显然非法的,必须得让 j j j和 k k k中的“1”岔开,这里判断用到一个小技巧,j & k == 0则意味着相同位置不会同时出现1。
最终,整块拼图的方案数存在了
f[m][0],0表示 ( 00...0 ) 2 (00...0)_2 (00...0)2,它意味着 m m m列不放小方格,前 m − 1 m-1 m−1列已经完全摆放好并且不伸出来的状态。那么意味着拼图完整。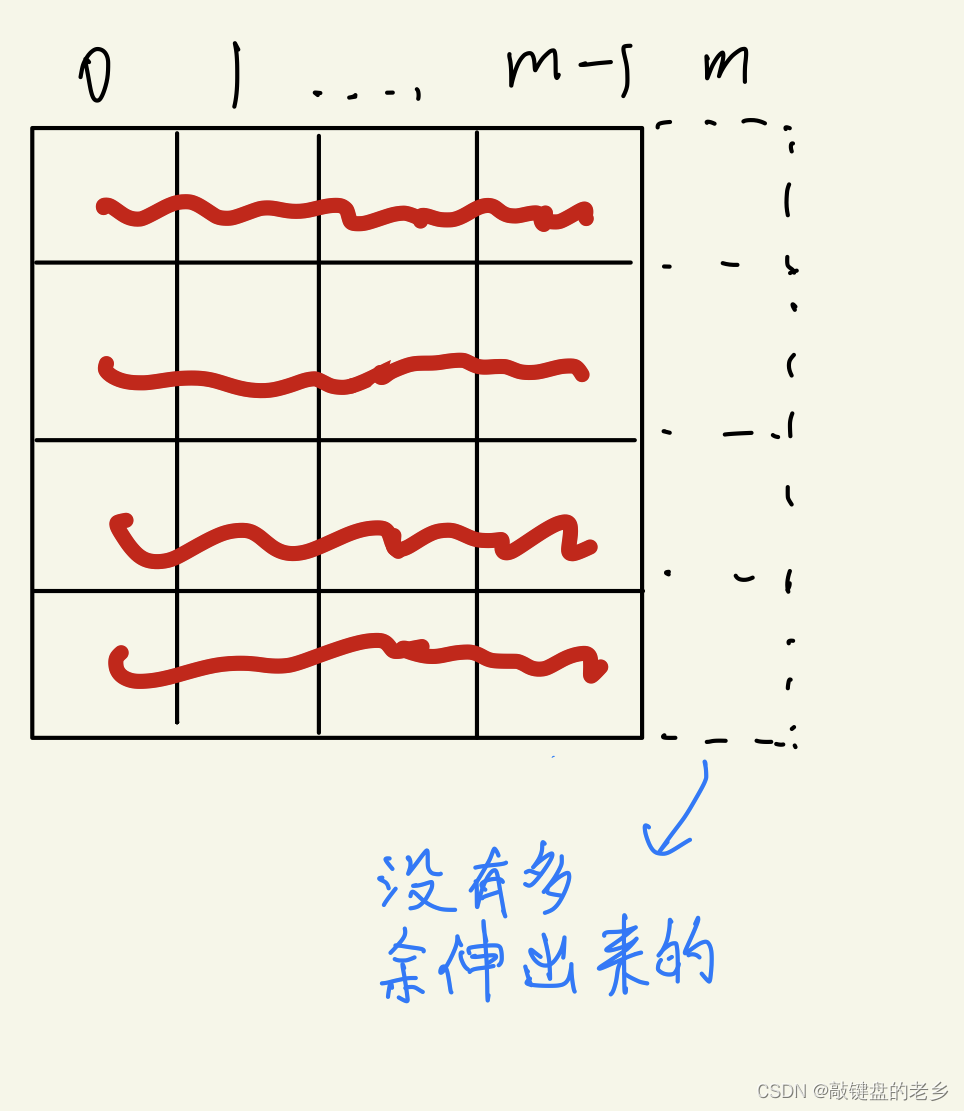
Code
#include#include using namespace std; typedef long long ll; const int N = 12, M = 1 << N; //N表示列数、M表示状态的范围(0b00...0 ~ 0b10...0) ll f[N][M]; //f[i][j]:第i列的状态为j时的方案数 bool st[M]; //st[j]映射状态j是否满足“没有奇数个连续的空格”这个条件 int n, m; int main(){ while(cin >> n >> m, n || m){ //第一步预处理,装填st数组 for(int i = 0;i < 1 << n;i ++){ //枚举每个状态 int cnt = 0; bool valid = true; for(int j = 0;j < n;j ++){ if((i >> j) & 1){ if(cnt & 1){ //如果有奇数个连续的空格 valid = false; break; } cnt = 0; } else cnt ++; } if(cnt & 1) valid = false; //统计最后一堆连续空格(如果有) st[i] = valid; } memset(f, 0, sizeof f); f[0][0] = 1; //因为没有-1列,第0列至少有一种摆放方案 for(int i = 1;i <= m;i ++) //枚举每一列 for(int j = 0;j < 1 << n;j ++) //枚举j,把j视作从i - 1列捅到i列的格子状态 for(int k = 0;k < 1 << n;k ++) //枚举k,把k视作从i - 2列捅到i - 1列的格子状态 if((j & k) == 0 && st[j | k]) f[i][j] += f[i - 1][k]; cout << f[m][0] << endl; } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
最短Hamilton路径
给定一张 n n n 个点的带权无向图,点从 0 ∼ n − 1 0∼n−1 0∼n−1 标号,求起点 0 0 0 到终点 n − 1 n−1 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 0 0 到 n − 1 n−1 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n n n。接下来 n n n 行每行 n n n 个整数,其中第 i i i 行第 j j j 个整数表示点 i i i 到 j j j 的距离(记为 a [ i , j ] a[i,j] a[i,j])。
对于任意的 x , y , z x,y,z x,y,z,数据保证 a [ x , x ] = 0 , a [ x , y ] = a [ y , x ] 并 且 a [ x , y ] + a [ y , z ] ≥ a [ x , z ] a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z] a[x,x]=0,a[x,y]=a[y,x]并且a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。数据范围
1 ≤ n ≤ 20 1≤n≤20 1≤n≤20
0 ≤ a [ i , j ] ≤ 1 0 7 0≤a[i,j]≤10^7 0≤a[i,j]≤107输入样例:
5 0 2 4 5 1 2 0 6 5 3 4 6 0 8 3 5 5 8 0 5 1 3 3 5 0- 1
- 2
- 3
- 4
- 5
- 6
输出样例:
18- 1
详细解释
这里有一篇写得很棒的解释👉 最短Hamilton路径(超详解)。
偷个懒吧hh。状态表示
f[i][j]: 所有从0走到j,经过的路径是i(二进制数)的最短距离。
举个例子:i = 11001、j = 4时,1表示走到,0表示没走到,那么状态i代表的路径就是0 —> 3 —> 4,那么f[0b11001][4]就代表从0走到4,路径是0 —> 3 —> 4的最短距离。
因此,答案就存在f[0b111...1][n - 1]=f[(1 << n) - 1][]n - 1里面。状态计算
状态计算用到的算法就很类似于 f l o y d floyd floyd算法,即
- 暴力地枚举每种可能的走法
i - 在
i的走法下,暴力地枚举每一个点j作为终点的情况 - 在
j作为终点的基础上,然后再暴力地枚举每一个点k(这个点也可以想象成 f l o y d floyd floyd里的那个k),目的是把k视作一个中间点(从位置上准确地讲,k是0走到j之前到达的最后一个点) - 然后经过各种
0 —> (一系列不包含终点 j 的点) —> k —> j路径来对f[i][j]进行松弛操作,也就是f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j])。其中i - (1 << j)对应的就是 “一系列不包含终点 j j j 的点”。
Code
#include#include using namespace std; const int N = 20, M = 1 << N; int w[N][N]; //距离矩阵 int f[M][N]; //f[i][j]:所有从0走到j,经过的路径是i(二进制数)的最短路径 int n; int main(){ cin >> n; for(int i = 0;i < n;i ++) for(int j = 0;j < n;j ++) cin >> w[i][j]; memset(f, 0x3f, sizeof f); f[1][0] = 0; for(int i = 0;i < 1 << n;i ++) //枚举所有的走法 for(int j = 0;j < n;j ++) //枚举j,将j认为是终点,当然了,是为了能将状态转移到n - 1这个点 if(i >> j & 1) //点在路径上的状态是1才说明“走到了”并进行处理 for(int k = 0;k < n;k ++) //枚举k,将k认为是走到j之前的最后一个点 if(i >> k & 1) //点在路径上的状态是1才说明“走到了”并进行处理 f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); //松弛操作 cout << f[(1 << n) - 1][n - 1] << endl; return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
-
相关阅读:
Python高光谱遥感数据处理与机器学习实践技术
LeetCode第39题-组合总和-java实现-图解思路与手撕代码
[附源码]java毕业设计基于servlet技术实现游戏娱乐平台
Qt 读写数据流文件(转 CppGuiProgrammingWithQt4)
关于Pytorch下载并进行部署
反激变压器计算方法_笔记
java计算机毕业设计交通非现场执法系统源码+mysql数据库+系统+lw文档+部署
前端给后端发请求,后端如何知道是已经登录的人发的请求还是未登录的人发的请求?
flink StandAlone 单机部署
GAN相关网络用什么归一化方法:BatchNorm?Weight Norm?Layer Norm?
- 原文地址:https://blog.csdn.net/weixin_53024141/article/details/127999599
