核磁共振成像学习笔记——从FID信号到K空间

在理想磁场环境下（没有不存在场不均匀性），对于一个没有梯度场的方块。


此时，RF pulse的两路正交信号（相位差为90°）对此方块进行激发，然后收取信号，我们可以得到由此方块产生的FID信号。


设此信号为S(t)，则此信号由Sc(t)与Ss(t)组成，分别组成S(t)的实部与虚部。

{Sc(t)=Mxye−t/T2cos(ωt)Ss(t)=Mxye−t/T2sin(ωt)

这是我们的接受线圈接收到的两组正交信号。
再利用欧拉公式

{cos(ωt)=eiωt+e−iωt2sin(ωt)=eiωt−e−iωt2i

使

S(t)=Sc(t)+iSs(t)

则

S(t)=Mxy∗e−t/T2∗e−iωt

此时，我们忽略衰减项e−t/T2，则

S(t)=Mxy∗e−iωt

这是我们对单个方块进行激发的结果，那么此时，引入梯度磁场进行空间定位。


根据拉莫尔进动(Larmor precession)

ω=γB

Phase encoding gradient和frequency encoding gradient的出现会使得这个方块内部的每个位置的进动频率ω发生变化。但需要注意Phase encoding gradient和frequency encoding gradient是不能够同时开启的(SE序列中)。然后，我们看自旋回波序列(SE)。

在接收信号前，分别开启了一段Phase encoding gradient和frequency encoding gradient。在接收信号的时候，frequency encoding gradient全程保持开启。
先进行公式推导，S(t)即为上文理想方块条件下推导得出的，我们将Mxy设定为ρ(x,y)表示方块中每个位置在加权设定后的信号强度，则

S(t)=∬

其中

\phi(x,y,t)={\gamma}\int_{0}^{t}{[G_x(t^{\prime})x+G_y(t)y]}dt^{\prime}

设定G_x为frequency encoding gradient，G_y为Phase encoding gradient，和序列图中保持一致，0至t为开始采样至实时采样的时间，SE序列图中的t_1和t_2为其中的两个t（这是一个变上限积分）。
令

\left\{ \begin{aligned} k_x=2\pi\int_{0}^{t}{G_x(t^{\prime})}dt^{\prime}\\ k_y=2\pi\int_{0}^{t}{G_y(t)}dt^{\prime} \end{aligned} \right.

则

S(t)=\iint{\rho(x,y)e^{-i2\pi[k_xx+k_yy]}}dxdy

即

S(k_x,k_y)=\iint{\rho(x,y)e^{-i2\pi[k_xx+k_yy]}}dxdy

至此，在数学上说明了S(t)与\rho(x,y)互为傅里叶变换对。这时，我们将方块分割为一个3*3的方块进行进一步的说明。

其中的数值为该位置对应的\rho(x,y)数值。
以S_c(t)信号为例，其组成的是S(t)中的实部，在没有进行空间编码前

根据SE序列的波形，先是进行了Phase encoding gradient

Phase encoding gradient改变的也是\omega，但作用了一段时间就停止了，相当于把纵向的各个单位以不同的\omega推了相同的时间，那么他们的相位\theta就发生了变化。并且，通过改变Phase encoding gradient的斜率，可以使得\theta的数值发生变化，对于一个3*3的方块，想要进行空间定位就要改变三次Phase encoding gradient斜率。
然后在收取数据的同时，进行frequency encoding gradient

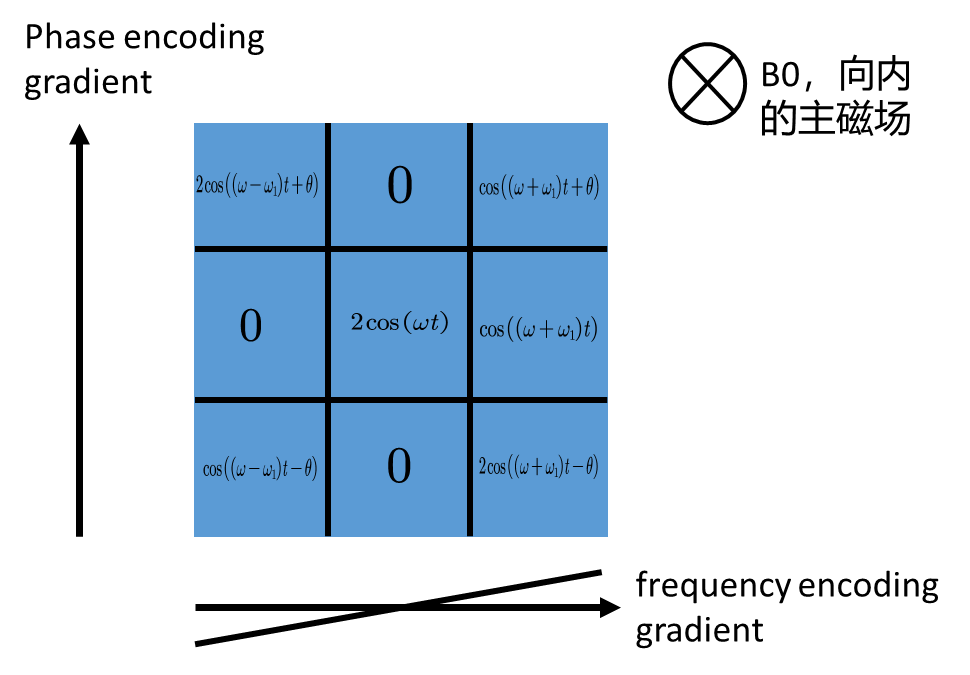
frequency encoding gradient同样改变了\omega，并且与收取信号同时进行，就此完成了区块的空间定位。通俗的来说，假设这些区块在一个环形的跑道进行赛跑，Phase encoding gradient就相当于在跑步开始之前，将同一个跑道上的每个跑者推到不同的起点上，frequency encoding gradient相当于使得不同跑道上的跑者有不同的跑步速度。
让我们回到公式

\left\{ \begin{aligned} k_x=2\pi\int_{0}^{t}{G_x(t^{\prime})}dt^{\prime}\\ k_y=2\pi\int_{0}^{t}{G_y(t)}dt^{\prime} \end{aligned} \right.

这里面的k_x与k_y就是位于K空间的xy坐标（注意t与t^{\prime}的区别）。G_y(t)就是Phase encoding gradient，在SE序列中每次都需要重新变化斜率，需要在y方向将区域分割成多少块，就需要变化多少次斜率，每次变化都需要经过一个TR。而G_x则保持不变，并且只需要增加采样点数就可以增加此方向的区块分割，不需要增加采样的时间。故我们使用SE序列进行图像重建的时候，最好将分块更多的方向对应frequency encoding gradient，因为每次Phase encoding gradient都需要消耗一个TR。这里我截取MRI,The Basics书中的一幅图说明这一点。

对于一个3*3的方块，哪边放在frequency encoding gradient都无所谓。但如果是一个128*256的方块，那么就需要将256的那条边放在frequency encoding gradient上，以减少重建时间。
参考:
[1]MRI From Picture to Proton
[2]MRI, The Basics
[3]MRI磁振影像學 盧家鋒
[4]MRI原理-信号 - lemon lelieven的文章 - 知乎 https://zhuanlan.zhihu.com/p/137255997
[5]【磁共振的K空间】 https://www.bilibili.com/video/BV1ch411e7Yc/?share_source=copy_web&vd_source=0e8c3fe50c67df43ceeb30f63e36eb0d