【算法系列】非线性最小二乘求解-直接求解法

系列文章目录

·【算法系列】卡尔曼滤波算法

·【算法系列】非线性最小二乘求解-直接求解法

·【算法系列】非线性最小二乘求解-梯度下降法

·【算法系列】非线性最小二乘-高斯牛顿法 

·【算法系列】非线性最小二乘-列文伯格马夸尔和狗腿算法 

系列文章

文章目录

        前言

        算法推导

        总结

---

前言

SLAM问题常规的解决思路有两种，一种是基于滤波器的状态估计，围绕着卡尔曼滤波展开；另一种则是基于图论（因子图）的状态估计，将SLAM问题建模为最小二乘问题，而且一般是非线性最小二乘估计去求解。

非线性最小二乘有多种解法，本篇博客介绍直接求解的方法。

---

算法推导

非线性最小二乘的一般形式如下：

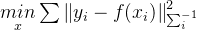
其中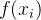是非线性函数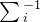，表示协方差矩阵

首先对f(x)进行线性化近似，这样就能把非线性最小二乘转化成线性最小二乘，然后直接求解线性方程就可以得到解。

一般线性化的方法都是使用泰勒展开进行线性化，对精度要求不高时尝尝采用一阶泰勒展开，在x0处进行泰勒展开：

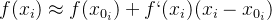
将展开后的式子带入到目标函数，并将协方差矩阵开方后放到平方运算中得到下式：

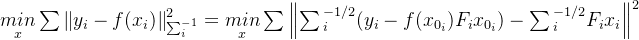
将前面可以求出的常数项整体用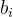表示，后面待求项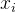的系数用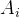表示整理一下得到：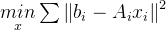

在理想情况下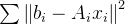，可以取到最小值0，就相当于其中的每一项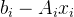取到最小值0，其实就是解下面这个线性方程组：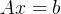

在平常求解线性方程组时直接两边左乘A的逆就求出解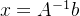，但A一般不可逆，这时往往求该方程组的数值解，一般使用的方法时Cholesky分解和QR分解。

Cholesky分解方法：

Cholesky分解是在原来的式子两边左乘A的转置，然后利用Cholesky分解将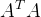分解成n×n的上三角矩阵R的乘积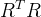，再令新的变量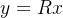，就得到了新的线性方程组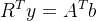

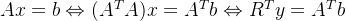
因为R是上三角矩阵，其转置后为下三角矩阵，第一行只有一个变量，行数越往下变量越多，于是从上到下很容易依次解出y，然后再解线性方程组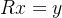，而这个方程组最后一行只有一个变量，自下而上也可以很容易的解出x，这样原方程组就可以求解出来了。

QR分解：

QR分解比Cholesky分解更加精准和稳定，利用QR分解将A分解为Q矩阵和R矩阵的乘积，其中Q是正交矩阵，R是上三角矩阵，然后在方程组两边同时左乘Q的逆对方程进行化简，如下：

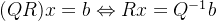
R是上三角矩阵，很容易就能求出x。

---

总结

在实际的SLAM问题中，非线性最小二乘很难找到合适的线性化方法，仅仅使用一阶泰勒展开进行近似有时会产生较大的误差；而且代价函数的误差往往也不能最小化到0值，所以直接求解的方法在现实中的应用存在诸多问题。

所以下面的博客将介绍优化的方法求解非线性最小二乘问题，这种方法在实践中是比较常用的。