计算机物联网控制11月9日第五章-重要5.3数控技术基础 *涉及到了真正的控制算法* 5.4PID控制算法

目录

5.3数控技术基础

5.3.-1概述

1.基本概念

2.数控系统构成

5.3-2数控原理

1.曲线分段

2.插值(或插补) 

3.绘图或加工

5.3-3数控系统分类

1.按控制方式分类

2.按系统结构分类

5.3-4运动控制系统

5.4数字PID控制算法

5.4-1标准数字PID控制算法

1.标准的PID

2.采样周期与控制周期的概念

3.PID增量算式

5.4-2数字PID控制算法的改进

1.理想微分PID与实际微分PID

2.微分先行PID控制算法("测量值微分")

3.积分分离PID算法

4.遇限切除积分PID算法

5.提高积分项积分的精度

5.4-3数字PID控制的参数整定

1.整定过程

2.采样周期的确定(一般规律)

3.基于偏差积分指标最小的整定参数法

4.试凑法

5.一些图像

比例增益对控制系统过渡过程的影响

积分时间对控制系统过渡过程的影响

微分时间对控制系统过渡过程的影响 

纯比例控制参数整定

比例积分控制参数整定

PID控制参数整定1

PID控制参数整定2

6.其他先进的自动整定方法

---

5.3数控技术基础

5.3.-1概述

1.基本概念

数字控制(NC)：用数字化信号对机床运动及其加工过程进行控制的一种方法；

数控系统：采用了数控技术的控制系统；

数控设备：采用了数控系统的设备；

计算机数控系统(CNC)：以计算机为核心的数控系统。

2.数控系统构成

5.3-2数控原理

1.曲线分段

——将如图所示曲线分割成若干段，可以是直线段，也可以是曲线段，图中分割成了三段即、和；

——把a、b、c、d四点坐标记下来并送给计算机。图形分割原则应保证险段所连的曲线与原图形误差在允许范围内；

——由图可见，显然采用 比要精确得多。

2.插值(或插补) 

插值(或插补) ：当给定a、b、c、d各点坐标x和y值之后，求得各坐标值间的中间值的数值；

直线插补：给定的两个基点之间用一条近似直线来逼近；

二次曲线插补：在给定的两个基点之间用一条近似曲线来逼近。

3.绘图或加工

——把插补运算过程中定出的各中间点，以脉冲信号形式去控制x、y方向上的步进电机，带动绘图笔、刀具等，绘出图形或加工所要求轮廓；

——每一个脉冲信号代表步进电机走一步，即绘图笔或刀具在x或y方向移动一个位置；

——对应于每个脉冲移动的相对位置称为脉冲当量，又称为步长，通常用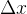和表示，且一般取。

5.3-3数控系统分类

1.按控制方式分类

点位控制数控系统：点位控制最简单，其运动轨迹没有特殊要求，运动时又不加工，它的控制电路只要具有记忆和和比较功能即可，不需要插补运算。

直线控制数系统：和点位控制相比，直线控制要进行直线加工，控制电路要复杂一些。

轮廓数控制系统：要控制刀具准确完成复杂的曲线运动，故控制电路复杂，且需要进行一系列的 插补计算和判断。

2.按系统结构分类

开环数控系统

——早期数控机床采用的数控系统，执行机构多采用步进电机或脉冲马达。数控系统将零件程序处理后，输出指令脉冲信号，驱动步进电动机，控制机床工作台移动。

——这种驱动方式不设置检测元件，指令脉冲送出后，没有反馈信息，容易掌握，调试维修方便，但控制精度和速度受到限制。

全闭环数控系统

——接受数控系统驱动指令同时，还接受工作台上检测元件测出的实际位置反馈信息，比较后根据差值进行修正，消除因传动系统误差引起的误差。 

——可获得高的加工精度，由于包含很多机械传动环节，会影响伺服系统的调节参数。因此全闭环系统的设计和调整都有较大困难，处理不好常会造成系统不稳定。主要用于高精度机床。

半闭环数控系统

将测量元件从工作台移到执行机构端，由于工作台不在控制环里，测量元件安装在执行机构端，环路短，刚性好，容易获得稳定的控制特性，广泛应用于各类连续控制的数控机床上。

5.3-4运动控制系统

5.4数字PID控制算法

5.4-1标准数字PID控制算法

proportional(比例)、integral(积分)、differential(微分)三者的缩写，在过程控制中，按误差信号的比例、积分和微分进行控制的调节器，简称PID调节器，是技术成熟、应用最为广泛的一种调节器。

1.标准的PID

  模拟调节器的比例增益；

 积分时间；

 微分时间；

 为偏差 e=0 时调节器的出，又称为稳态工作点。

2.采样周期与控制周期的概念

模拟PID调节规律的离散化

在控制器的采样时刻t=KT时：

因此PID的数字算式如下式：

数字PID又可写成：（又称PID位置算式）

 

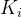  称为积分系数；

 称为微分系数。

 PID位置算式的问题：由积分项的存在所产生：

3.PID增量算式

另一种形式： 

增量PID算法的优点：

(1)编程简单

(2)数据可以递推使用

(3)占用内存少

(4)速度快

求得K 采样时刻计算机的实际输出控制量为：

5.4-2数字PID控制算法的改进

实际微分PID控制算法

微分的作用

理想微分的PID算法

1.理想微分PID与实际微分PID

——在单位阶跃输入时，它们输出的控制作用：

——其区别在于实际微分多了个一节惯性环节

因为 为理想PID的输出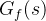，   是一阶惯性环节。

故：

——经计算，可得实际微分位置型控制算式：

 ——实际微分增量型控制算式：

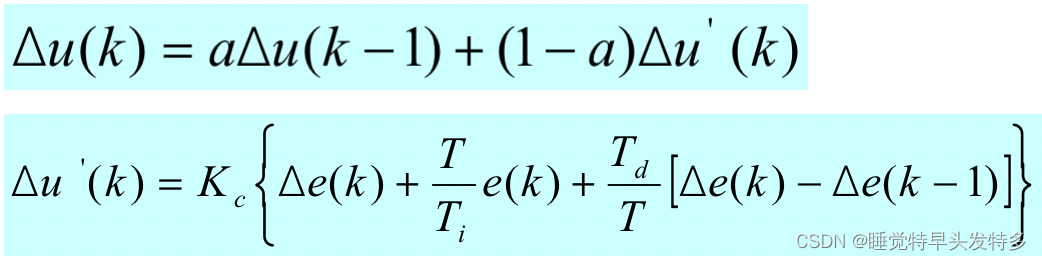
实际微分的其它形式： 

Gf(s)为一阶超前/一阶滞后环节，或将理想微分作用改为微分/一阶惯性环节。

2.微分先行PID控制算法("测量值微分")

出发点：避免因给定值变化给控制系统带来超调量过大、调节阀动作剧烈的冲击。

特点：只对测量值(被控量)进行微分, 而不对偏差微分, 也即对给定值无微分作用。

偏差计算：

正作用：e(k)=y(k)-r(k)

反作用：e(k)=r(k)-y(k)

微分先行PID控制算法示意图

3.积分分离PID算法

提出背景：积分作用会产生较大超调和振荡

基本思想

当|e(k)|>A时，用P或PD控制；

当|e(k)|<=A时，用PI或PID控制。

注意：

(1)A值要适当选取；

(2)Kc应根据积分作用是否起作用而变化。

积分分离PID算法示意图

 

4.遇限切除积分PID算法

——执行机构机械性能与物理性能的约束

——积分饱和

——该算法是抑制积分饱和的方法之一

基本思想：一旦计算出的控制量u(k)进入饱和区，一方面对控制量输出值限幅；另一方面增加判别程序，算法中只执行削弱积分饱和项的积分运算，而停止增大积分饱和项的运算。

5.提高积分项积分的精度

积分项的作用：比较重要

提高积分项的运算精度的方法:

初始方法：

改进方法：

模拟调节器实现的微分作用

理想微分作用的实际缺陷

实际微分作用

5.4-3数字PID控制的参数整定

1.整定过程

先按模拟PID控制参数整定方法来选择，然后在适当调整，并考虑采用周期对整定参数的影响

2.采样周期的确定(一般规律)

 稳定边界法(临界比例度法)

动态特性法（响应曲线法） 

 

3.基于偏差积分指标最小的整定参数法

常用三种指标：

最佳整定参数应使这些积分指标最小，不同积分指标所对应的系统输出被控变量响应曲线稍有差别。

一般情况下，ISE指标的超调量大，上升时间快；IAE指标的超调量适中，上升时间稍快；ITAE指标的超调量小，调整时间也短。 

4.试凑法

一般规律：

——增大比例系数Kc一般将加快系统的响应，使系统的稳定性变差。

——减小积分时间Ti，将使系统的稳定性变差，使余差（静差）消除加快。

——增大微分时间Td，将使系统的响应加快，但对扰动有敏感的响应，可使系统稳定性变差。  

试凑时，可参考上述参数对控制过程的影响趋势，对参数实行先比例，后积分，最后微分的整定步骤。

整定步骤：

(1)首先整定比例部分。将比例系数由小变大，观察相应响应，直到得到反应较快，超调较小的响应曲线。若系统静差较小，满足要求可采用纯比例控制。

(2)如果纯比例控制有较大余差，则需要加入积分作用。积分时间从大变小，同时调整比例增益，使系统保持良好的动态性能，反复调整比例增益和积分时间，以得到满意的动态性能。

(3)若使用比例积分控制，反复调整仍达不到满意的效果，则可加入微分环节。在整定时，微分时间从小变大，相应调整比例增益和积分时间，逐步试凑，以得到满意的动态性能。

常用口诀：

​​​​​​​

​​​​​​​参数整定找最佳，从小到大顺序查

先是比例后积分，最后再把微分加

曲线振荡很频繁，比例度盘要放大

曲线漂浮绕大湾，比例度盘往小扳

曲线偏离回复慢，积分时间往下降

曲线波动周期长，积分时间再加长

曲线振荡频率快，先把微分降下来

动差大来波动慢，微分时间应加长

理想曲线两个波，前高后低4比1  

一看二调多分析，调节质量不会低

5.一些图像

比例增益对控制系统过渡过程的影响

积分时间对控制系统过渡过程的影响

微分时间对控制系统过渡过程的影响 

纯比例控制参数整定

比例积分控制参数整定

PID控制参数整定1

PID控制参数整定2

6.其他先进的自动整定方法

基于继电反馈控制(relay feed back control)

基于模式识别(pattern recognition)

基于专家系统原理(expert system)