数据结构入门4-2（广义表、例题）

目录

注

广义表的定义

广义表的存储结构

1. 头尾链表的存储结构

2. 扩展线性链表的存储结构

例题：病毒感染检测

---

注

        本笔记参考：《数据结构（C语言版）（第2版）》

---

广义表的定义

||| 定义：广义表是线性表的推广，又称列表。

        一般地，广义表被记作：

  习惯上使用大写字母表示广义表的名称，用小写字母表示原子。

        从上述表示可知，在描述一个广义表时又会用到广义表的概念，因此，广义表的定义实际上是一个递归的定义，例如：

        由此，可得结论：

1. 广义表是一个多层次的结构，这种结构可以通过图像进行表示（图像来自上述例子）：

   

2. 广义表可以为其他广义表所共享。例如上图中的 D = (A, B, C) ，此处不必列出子表的值，而仅需引用子表的名称；
3. 广义表可以是一个递归的表，或者是广义表可以是其自身的一个子表。如：E = (a, E) 。

        因为本身结构的复杂性，广义表的各种运算较线性表相比要更加困难，在这之中，有两个最重要的运算：

  1. GetHead(LS)

• 作用：取表头；
• 返回值：非空广义表 的第一个元素（一个原子\子表）。

  2. GetTail(LS)

• 作用：取表尾；
• 返回值：除表头外，由其余元素构成的表（返回值一定是一个广义表）。

        例如：

( ) 和 (( )) 的区别

  在广义表中，( ) 和 (( )) 是不同的：

• ( ) ：表示空表，长度为 0 ；
• (( )) ：分解可得 表头 和 表尾 均为空表( )，长度为 1 。

广义表的存储结构

        由于广义表的数据元素更为复杂（原子\子表），使用顺序存储结构较难以表达，所以通常使用的是链式存储结构。常用的链式存储结构有两种：

• 头尾链表的存储结构；
• 扩展链表的存储结构。

1. 头尾链表的存储结构

        根据广义表的数据元素，可以得出需要的两种结构的节点：

• 表结点：用以表示广义表；
• 原子结点：用以表示原子。

        通过函数GetTail( )的定义可知：非空广义表可被分解为表头和表尾。由此可知，一对确定的表头和表尾可以唯一确定广义表。

        节点的结构如下：

         广义表的头尾链表存储形式如下：

#define AtomType int		// AtomType 可自定义
typedef enum
{
	ATOM,	//ATOM == 0：原子
	LIST	//LIST == 1：子表
}ElemTag;
typedef struct GLNode
{
	ElemTag tag;			//公共部分，用于区别原子结点和表结点
	union					//原子节点和表节点的联合部分
	{
		AtomType atom;		// atom 是原子结点的值域
		struct
		{
			struct GLNode* hp, * tp;	// ptr.hp 和 ptr.tp 分别指向表头和表尾
		}ptr;				// ptr 是表结点的指针域
	};
}*Glist;					//广义表类型

        在上述这种结构的存储中存在如下的几种情况：

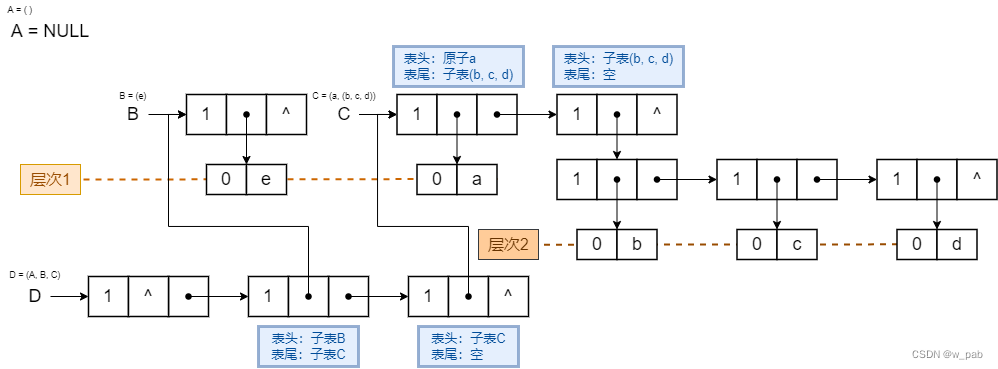
【分析】

• 除空表外（其表头指针为空），对于任何非空广义表，其表头指针均指向一个表结点。该表结点的：
  • hp域指向广义表的表头（是一个原子结点/表结点）；
  • tp域指向广义表的表尾（当表尾为空时，指针为空；当表尾不为空时，指针指向的必定是一个表结点）。
• 从上图可知，对于广义表D而言：
  • 原子 a 和 e 在同一层，b、c 和 d 则比其低一层；
  • B 和 C 是同一层的子表。
• 最高层的表结点的个数即为广义表的长度。

---

2. 扩展线性链表的存储结构

        在这种结构中，原子结点和表结点类似，均由三个域组成：

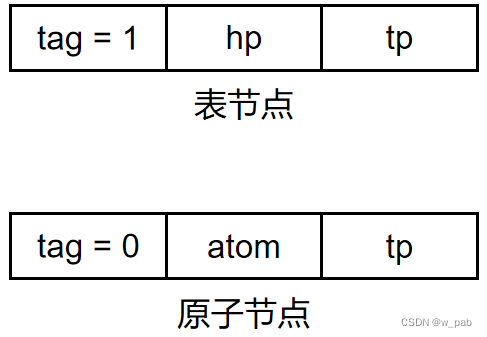
        这种存储结构可以这样表示：

例题：病毒感染检测

【要求】

        给定患者的DNA序列和病毒的DNA序列，要求检测出某种病毒DNA序列是否在患者的DNA序列中出现过。

【注意】

        给定的DNA序列都是由一些字母组成的字符串的序列。该问题本质上是一个字符串的模式匹配问题。

  ps：病毒的DNA序列是环状的。这意味着其不同于传统的模式匹配算法，需要对传统算法进行改进。

【代码：此处使用BF算法】

  下方代码使用string类进行存储操作，也可使用其他类型。

void Virus_detection()
{//利用BF算法实现病毒检测
	ifstream inFile("病毒感染检测输入数据.txt");	//inFile：负责读取数据
	ofstream outFile("病毒感染检测输出数据.txt");	//outFile：负责输出数据
 
	string ch_Virus;
	string ch_Person;
	string Vir;
	int num = 0;
	inFile >> num;					//读取待检测的任务数
                                    //默认情况下，inFile的读取直到遇到空格才会结束
 
	while (num--)
	{
		inFile >> ch_Virus;
		ch_Virus = '#' + ch_Virus;	//读取病毒DNA序列，从下标[1]开始存放
		inFile >> ch_Person;
		ch_Person = '#' + ch_Person;//读取人的DNA序列
		Vir = ch_Virus;				//将病毒DNA暂存，以备输出
 
		int flag = 0;				//用来标识是否匹配，初始为0，匹配后为非0
		int m = ch_Virus.length();	//病毒DNA序列的长度为m
 
		int j;
		for (j = 1; j <= m; j++)
			ch_Virus += ch_Virus[j];		//将病毒字符串的长度扩大到原本的2倍
		ch_Virus += '\0';
 
		int i;
		for (i = 0; i < m; i++)		//以此取出每一个长度为m的病毒DNA环状字符串
		{
			string ch_Temp = "#";	//使用ch_Temp暂时存储
			for (j = 1; j < m; j++)
				ch_Temp += ch_Virus[i + j];
			ch_Temp += '\0';		//添加结束符号
 
			flag = Index_BF(ch_Person, ch_Temp, 1);		//进行模式匹配
			if (flag)				//匹配成功，结束循环
				break;
		}
		if (flag)
			outFile << Vir << " " << ch_Person << " " << "Yes" << endl;
		else
			outFile << Vir << " " << ch_Person << " " << "No" << endl;
	}
}

【分析】

  由于病毒的DNA序列是环状的，为了取得这种DNA序列上每串可行的长度准确的字符串，可将存储病毒序列的DNA序列的字符串长度扩大到原本的两倍（即将病毒DNA序列连续存储两次）。

int j;
for (j = 1; j <= m; j++)
	ch_Virus += ch_Virus[j];		//将病毒字符串的长度扩大到原本的2倍

设人的DNA序列长度为 n ：

        对于每一个待检测的任务而言，该算法都需要执行 m 次模式匹配。因此，使用BF算法的时间复杂度为 O(m * n) 。对于每一个待检测的任务，其时间复杂度为 O(m * m * n) 。

        如果再算上待检测的任务的数量 num ，可得上述算法的时间复杂度为 O(num * m * m * n) 。