GWAS中的effect与数量遗传学中的替换效应

虽然，我早就知道GWAS分析中的effect值，就是数量遗传学的基因中的替换效应，但是一直没有仔细阅读相关材料。今天通过阅读数量遗传学的教程，理解了这个概念，真好。

1. GWAS中的effect

就是GWAS中的回归系数，effect，beta，都是一个意思。

因为GWAS分析汇总，单点检测，类似回归分析，effect就是SNP回归系数beta，p值就是SNP的P-value。

比如数据：

用R语言拟合模型：

mod_M7 = lm(phe.V3 ~ M7_1,data=dd)
summary(mod_M7)
1
2

这里的M7位点，effect是1.394，p值是0.29。

下图用GWAS的GLM模型展示，两者结果是一致的。

2. 数量遗传学中的替换效应

2.1 加性效应和显性效应

首先，先看一下加性效应和显性效应的定义：

举个栗子比如：

• A2A2的平均值是：20
• A1A2的平均值是：17
• A2A2的平均值是：10

那么：

• 平均值是m = （10+20）/2 =15
• 加性效应的值是a = (20-10)/2 =5
• 显性效应的值是d = 17-15=2

2.2 期望和方差

假定一个位点的次等位基因频率是p，主等位基因频率是q，而且该位点满足哈温平衡，所以：

整体均值为：

整体方差：

2.3 等位基因平均效应

一种定义等位基因效应的方法，是利用后代群体的平均表现与随机交配群体均值的离差进行计算。
以等位基因A1为例，把它视为配子，与群体中其他配子随机结合产生一个后代群体，其他配子基因型既有A1也有A2，它们的频率分别为p和q。因此，配子A1产生后代群体中的基因型有A1A1和A1A2两种，频率也分别为p和q。根据配子A1后代群体的基因型频率，就能得到后代群体的均值为pa+qd，从中减去随机交配群体的均值μ，就得到等位基因A1的效应 。
类似地，我们还可以得到等位基因A2平均效应 。对于复等位基因，可用同样的方法定义它们的平均效应。

2.4 替换效应(substitution effect)

育种过程中，当选择有利于某个等位基因时，常意味着有利等位基因对另一个不利等位基因的替换。因此，有必要研究等位基因的替代效应（effect of an allele substitution）。假定我们可以把随机挑选的等位基因A2变为A1，中选个体的基因型可能是A1A2也可能是A2A2，频率分别为p和q。把A1A2变为A1A1后，基因型值从d变为a，替换前后的效应变化为a-d；把A2A2变为A1A2后，基因型值从-a变为d，替换前后的效应变化为a+d。因此得到平均基因替换效应的表达式。

基因平均效应和替换效应的关系：

上面资料来源王健康老师的PPT内容：第8章 随机交配群体的遗传分析

3. 用基因型数据计算

3.1 基因频率

首先，看一下基因频率：

• p为：0.1693
• q为：0.8307

也可以根据AA，AT，TT的个数，手动计算：

3.2 加性效应和显性效应

这里，用AA，AT，TT平均表型值计算：

计算的结果：

• m：2.316
• a：2.316
• d：1.804

3.3 基因效应和替换效应

注意，如果要手动计算的替换效应和回归分析计算的回归系数，需要满足哈温平衡。这里位点不符合哈温平衡，所以手动计算的替换效应和回归分析的beta值有差别。

4. 替换效应和回归系数等价推导

下面介绍一下相关的推导。

把SNP的分型转为0-1-2的X变量，将表型数据为Y变量，那么回归系数的公式可以推导为替换效应的组成。

上图中，X是编码为0-1-2的SNP，Y是每个基因型0-1-2的表型值。比如：

如果我们对value为Y，SNP为x，计算回归系数：
b = cov(X,Y)/var(X)，就可以推导为：b = alpha，截距为：u - 2palpha

结论：回归系数就是替换效应。

5 模拟数据演示

计算公式：

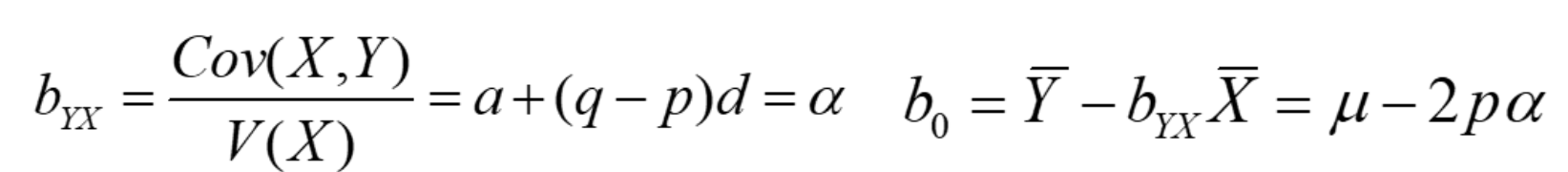
5.1 小数据演示

我们模拟一个符合哈温平衡的位点，p=0.5，q=0.5，n=12个：

计算不同分型的平均数：

• A2A2 = 10.7
• A1A2 = 18.2
• A1A1 = 31
  

那么加性效应和显性效应为：

• m = (31+10.7)/2 = 20.85
• a = 31-20.85 = 10.15
• d = 18.2 -m = -2.65

替换效应为：
a + (p - q)d = 10.15
截距为：
u = 19.5
截距 = 19.5 - 20.5*10.15 = 9.35

可以看出，计算出的回归系数为：10.16，截距为9.33，结果基本一致。

5.2 大数据演示

# 假定p为0.8，q为0.2，a=10,m =30,d=5,
# 那么分型为0的为20，分型为1的为35，分型为2的为40
# 那么分型为0的频率为0.64，分型为1的频率为0.32，分型为2的频率为0.04
# 总模拟个数为1000，标准差为5
rm(list=ls())
set.seed(123)
AA = data.frame(SNP = rep(0,640),y = rnorm(640,20,5))
AT = data.frame(SNP = rep(1,320),y = rnorm(320,35,5))
TT = data.frame(SNP = rep(2,40),y = rnorm(40,40,5))

dd = rbind(AA,AT,TT)
head(dd)
str(dd)
table(dd$SNP)

mod = lm(y ~ SNP,data=dd)
summary(mod)


## 手动计算
mu = mean(dd$y);mu
a=10;d=5;p=0.8;q=0.2 
beta = a + (p-q)*d;beta
beta_0 = mu - 2*q*beta;beta_0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

回归计算的回归系数和截距为：

• 截距：20.6
• 回归系数：12.9989
  

手动计算基因的替换效应：

• 截距为：20.61
• 回归系数为：13
  
  两者结果完全一致。

5. 替换效应和育种值

一个个体的育种值，就是他的后代群体，相对于整个亲本群体的差异。比如一个个体的育种值是0.5，那就是说他的后代会比群体的整体平均值高0.3，如果育种值是0，那就是后代的平均值和群体一致。所以，我们要选择blup值大的个体，因为它的后代会高于群体的平均值。

因此，基因型A1A1、A1A2和A2A2的育种值分别为A11=2α1， A12=α1 +α2和A22=2α2 。统一起来，各种基因型的育种值表示为：

• A11 = 2*alpha1
• A12 = alpha1 + alpha2
• A22 = alpha2
  注意，这里的alpha1是等位基因1的平均效应，alpha2是等位基因2的平均效应。

所以，这里，就可以理解为数量遗传学的替换效应就和GWAS分析的效应值联系到了一起。

根据上面的公式，我们就可以根据每个位点的效应值，计算单个SNP的育种值，加性效应和显性效应。