• Chapter 14 主题模型

    1 LDA模型

    1.1 LDA的应用方向

    信息提取和搜索（语义分析）；文档分类、聚类、文章摘要、社区挖掘；基于内容的图像聚类、目标识别（以及其他计算机视觉应用）；生物信息数据的应用

    1.2 LDA出现的原因

    前文提到的“朴素贝叶斯”可以胜任许多文本分类问题，但是无法解决一词多义（花：花朵和花费）和多词一义（陛下：天子和皇上）的问题·。因此可以通过增加“主题”的方式，一定程度上解决这些问题。

    针对一词多义的情况：在主题模型中一个词可能被映射到多个主题中。

    针对多词一义的情况：在主题模型中多个同意思的词可能被映射到某个主题的概率很高。

    2 Beta分布-Dirichlet分布

    2.1 Beta分布介绍

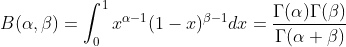
    Beta分布的概率密度为：f(x)=\left\{\begin{matrix} \frac{1}{B(\alpha ,\beta )x^{\alpha -1}(1-x)^{\beta -1}},x\in [0,1]\\ 0,others \end{matrix}\right.，其中系数B为：B(\alpha ,\beta )=\int_{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx=\frac{\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}

    PS:\Gamma函数的介绍

    \Gamma函数是阶乘在实数上的推广:\Gamma (x)=\int_{0}^{+\infty }t^{x-1}e^{-t}dt=(x-1)!

    由此：\Gamma(x)=(x-1)\Gamma (x-1)\Rightarrow \frac{\Gamma (x)}{\Gamma (x-1)}=x-1

    2.2 Beta分布的期望

    E(x)=\int_{0}^{1}x\cdot \frac{1}{B(\alpha ,\beta )}x^{\alpha -1}(1-x)^{\beta -1}dx= \frac{1}{B(\alpha ,\beta )}\int_{0}^{1}x^{(\alpha+1)-1 }(1-x)^{\beta -1}dx=\frac{B(\alpha +1,\beta )}{B(\alpha ,\beta )}=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}/\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha +1)\Gamma (\beta )}=\frac{\alpha }{\alpha +\beta }

    2.3 共轭先验分布相关介绍

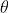    由于x为给定样本，P(x)有时被称为“证据”，仅仅是归一化因子，如果不关心P(\theta |x)的具体值，只考察\theta取何值时后验概率P(\theta |x)最大，所以省去分母：

    P(\theta |x)=\frac{P(x |\theta )P(\theta )}{P(x)}\propto P(x |\theta )P(\theta )

    在贝叶斯概率理论中，如果后验概率P(\theta |x)和先验概率P(\theta )满足同样的分布律（即两者概率相等），那么先验分布和后验分布叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

    • 二项分布和先验问题：投掷一个非均匀硬币，可以使用参数为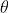\theta的伯努利模型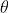，\theta为硬币正面的概率，那么结果x的分布形式为：P(x|\theta )=C_{n}^{k}\cdot \theta ^{k}\cdot (1-\theta )^{n-k}；两点分布/二项分布的共轭先验是Beta分布，它具有两个参数\alpha,\beta，其分布形式为P(\theta |\alpha ,\beta )=\left\{\begin{matrix} \frac{1}{B(\alpha ,\beta )}\theta ^{\alpha -1}(1-\theta )^{\beta -1},\theta \in [0,1]\\ 0,others \end{matrix}\right.
    • 先验概率和后验概率的关系：

    先验概率——P(x|\theta )=C_{n}^{k}\cdot \theta ^{k}\cdot (1-\theta )^{n-k}

    Beta分布——P(\theta |\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}\theta ^{\alpha -1}(1-\theta )^{\beta -1}

    后验概率——P(\theta |x)=\frac{P(x|\theta )\cdot P(\theta )}{P(x)} \propto P(x|\theta )\cdot P(\theta )=(C_{n}^{k}\theta ^{k}(1-\theta )^{n-k})\cdot(\frac{1}{B(\alpha ,\beta )}\theta ^{\alpha -1}(1-\theta )^{\beta -1})=\frac{C_{n}^{k}}{B(\alpha ,\beta )}\theta ^{(k+\alpha )-1}(1-\theta )^{(n-k+\beta )-1}\propto \frac{1}{B(k+\alpha ,n-k+\beta )}\theta ^{(k+\alpha )-1}(1-\theta )^{(n-k+\beta )-1}

    后验概率是参数为(K+\alpha,n-k+\beta )的Beta分布，即：伯努利分布/二项分布的共轭先验是Beta分布。

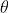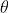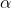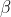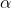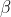    分析：参数\alpha ,\beta是决定参数\theta的参数，即超参数；我们可以看到参数\theta的指数是由\alpha ,\beta ,k,n-k共同决定的；这个指数在投硬币实验中的实践意义——投币过程中，正面朝上的次数，\alpha和\beta先验的给出了在没有任何实验前提下，硬币朝上的概率分配，因此\alpha和\beta可被称为“伪计数”。

    2.4 共轭先验的直接推广

    从Beta分布推广至Dirichlet分布：

    f(\overrightarrow{p}|\overrightarrow{\alpha })=\left\{\begin{matrix} \frac{1}{\Delta (\overrightarrow{\alpha })}\prod_{k=1}^{K}P_{k}^{\alpha _{k}-1},P_{k}\in [0,1]\\ 0,others \end{matrix}\right.

    简记为：Dir(\overrightarrow{p}|\overrightarrow{\alpha })=\frac{1}{\Delta (\overrightarrow{\alpha })}\prod_{k=1}^{K}P_{k}^{\alpha _{k}-1}，其中：\Delta (\overrightarrow{\alpha })=\frac{\prod_{k=1}^{K}\Gamma (\alpha _{k})}{\Gamma (\sum_{k=1}^{K}\alpha _{k})}

    由Beta分布的期望可推广至Dirichlet分布的期望为：E(p_{i})=\frac{\alpha _{i}}{\sum_{k=1}^{K}\alpha _{k}}

    3 Dirichlet分布分析

    3.1 Dirichlet分布

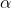    公式：Dir(\overrightarrow{p}|\overrightarrow{\alpha })=\frac{1}{\Delta (\overrightarrow{\alpha })}\prod_{k=1}^{K}P_{k}^{\alpha _{k}-1}

    \alpha是参数变量，共有K个；

    定义在x_{1},x_{2},...,x_{K-1}维上：x_{1}+x_{2}+...+x_{K}=1且x_{1},x_{2},...,x_{K-1}>0且定义在(K-1)维的单纯形上，其他区域的概率密度为0。

    3.2 对称Dirichlet分布

     参数分析：

    4 LDA的解释

    4.1 说明

    共有m篇文章，一共涉及了K个主题；

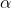    每篇文章（长度为N_{m}）都有各自的主题分布，主题分布是多项分布，该多项分布的参数服从Dirichlet分布，该分布的参数是\alpha；

    每个主题都有各自的词分布，词分布为多项分布，该多项分布的参数服从Dirichlet分布，该分布的参数是\beta；

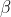    对于某篇文章中的第n个词，首先从该文章的主题分布中采样一个主题，然后在这个主题对应的词分布中采样一个词。不断重复这个随机生成过程，直到m篇文章全部完成上述过程。

     图中字母的解释：

    K——主题个数

    M——文档总数

    N_{m}——第m个文档的单词总数

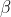    \beta——每个Topic下词的多项分布的Dirichlet先验参数，事先给出

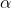    \alpha——每个文档Topic的多项分布的Dirichlet先验参数，事先给出

    zmn——第m个文档中第n个词的主题

    wmn——m个文档中的第n个词

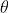    \theta——隐含变量，表示第m个文档下的Topic分布，k维（k维）

    \varphi——隐含变量，表示第k个Topic下词的分布，v维（v为词典中term总数）

    由图写出联合分布：

    4.2 Gibbs Sampling

    初始时，随机给文本中的每个词分配主题z^{(0)}，然后统计每个主题z下出现词t的数量以及每个文档m下出现主题z的数量，每一轮排除当前词的主题分布。根据其他所有词的主题分布估计当前词分配各个主题的概率。直到每个文档的主题分布和每个主题的词分布收敛为止。

    p(z_{i}=k|\overrightarrow{z_{j}},\overrightarrow{w})\propto \frac{n_{k,j}^{t}+\beta _{t}}{\sum_{t=1}^{v}n_{k,j}^{t}+\beta _{t}}(n_{m, j}^{k}+\alpha _{k})，其中z_{j}表示除了z_{i}词以外属于该主题的其他词。

    当\beta _{t}近似于0时：
    表示某个词z_{i}属于k主题的概率与当前其它属于k主题的词z_{j}的个数除以这些词的总数成正比，类似频率。

     4.2 主题个数的确定

    4.3 概率分布的困惑度/复杂度Perplexity

    4.4  困惑度/复杂度Perplexity与主题模型

     ps:一个网页i的重要度可以使用指向网页i的其他网页j的重要度加权得到。

    D(P_{i})=(1-d)+d\cdot \sum_{j\epsilon In(P_{i}) }\frac{1}{|Out(P_{j})|}\cdot D(P_{j})

    其中：

    D(P_{i})——网页i的重要性

    d——阻尼系数

    In(P_{i})——指向网页i的网页集合

    Out(P_{j})——网页j指向的网页集合

    当网页换成句子时，仅需考虑将“链接”加权：

    D(S_{i})=(1-d)+d\cdot \sum_{j\epsilon In(S_{i})}\frac{similar(S_{j},S_{i})}{\sum_{k\epsilon Out(S_{j})similar(S_{j},S_{k})}}\cdot D(S_{j})

     5 LDA总结

    • LDA可以很好得解决一词多义和多词一义的问题。
    • LDA用于短文档的效果是不明显的。
    • LDA可以和其他算法相结合。首先使用LDA将长度为N_{i}的文档降维到K维（主题的数目），同时给出每个主题的概率（主题分布），从而可以使用if-idf继续分析或者直接作为文档的特征进入聚类或者标签传播算法——用于社区发现等问题。

    6 实践

    背景：计算聊天记录中每个QQ号以及众人感兴趣的话题。

    步骤：

    （1）获取QQ群聊天记录：txt文本格式。

    （2）整理成“QQ号/时间/留言”的规则形式

    • 正则表达式
    • 清洗特定词，例如：表情、@XX
    • 使用停止词库
    • 获得csv表格数据

     

    （3）合并相同QQ号的留言

    （4）LDA模型计算主题

    （5）计算每个QQ号以及众人感兴趣的话题。

  • 相关阅读:
    element table 二次封装
    【机器学习】Kmeans聚类算法
    Android 基础知识4-1 用户界面简介VIewGroup、Onclick事件处理
    一个 Angular 程序员两年多的远程办公经验分享
    【AUTOSAR-RTE】-4-Port和Interface以及Data Type
    Mysql编译安装和yum安装
    一个免费开源自托管的机器翻译项目，支持API接口
    httprunnet自动化测试实战
    Java进阶——如何查看Java字节码
    专访黄文斌丨中专文凭的他，辞掉了9年的国企“铁饭碗”
  • 原文地址：https://blog.csdn.net/qwertyuiop0208/article/details/126196080