-
2022学年第一学期郑州大学ACM招新赛&选拔赛
A SW的与众不同数组 — 签到
一共n个数, 用set无重复值的性质统计一下有几个不同的数,记为 res
n - res 如果是偶数 每次删除两个刚好可以,如果是奇数需要再删除一个不重复的数完成对应操作#include#include using namespace std; void solve() { int n; cin >> n; set<int> mp; for(int i = 0, x; i < n; i ++) cin >> x, mp.insert(x); int res = mp.size(); if((n - res) % 2 == 1) res --; cout << res << '\n'; } signed main() { int T; cin >> T; while(T --) solve(); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
B WASD机器人 — 暴力/ 数学推导
暴力写法:
直接暴力枚举 最后成功到达终点的 串中的
L/R的数量,这样的话 L, R, U, D的数量全都可以确定下来了,然后每次更新答案,取最小值#include#include using namespace std; signed main() { string s; cin >> s; int n = s.size(); int x, y; cin >> x >> y; if(abs(x) + abs(y) > s.size()) return puts("-1"), 0; // 现有的 l, r, u, d 的数量 int nl = 0, nr = 0, nu = 0, nd = 0; for(auto c : s) { nl += c == 'L'; nr += c == 'R'; nu += c == 'U'; nd += c == 'D'; } int res = n; // 枚举最后结果中 l, r 数量 此时 u, d 数量也确定了 int l, r, u, d; for(int i = 0; i <= n; i ++) { if(x > 0) l = i, r = x + i; else l = -x + i, r = i; int dt = (n - l - r - y) / 2; if(y > 0) u = y + dt, d = dt; else u = dt, d = -y + dt; if(l < 0 || r < 0 || d < 0 || u < 0 ) break; int sum = abs(nl - l) + abs(nr - r) + abs(nu - u) + abs(nd - d); res = min(res, (sum + 1) / 2); } cout << res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
数学写法 放上吕翊加大佬的推导过程



#include#include using namespace std; int sum[5]; int main() { string s; cin >> s; for (int i = 0; i < (int)s.size(); ++ i) { if (s[i] == 'R') ++ sum[1]; if (s[i] == 'L') ++ sum[2]; if (s[i] == 'U') ++ sum[3]; if (s[i] == 'D') ++ sum[4]; } int tx, ty; cin >> tx >> ty; if (abs(tx) + abs(ty) > sum[1] + sum[2] + sum[3] + sum[4]) return puts("-1"), 0; if (tx < 0) { tx = -tx; swap(sum[1], sum[2]); } if (ty < 0) { ty = -ty; swap(sum[3], sum[4]); } int ans = 0; if (sum[1] + sum[2] < tx) ans += tx - sum[1]; else ans += (abs(sum[1] - sum[2] - tx) + 1) / 2; if (sum[3] + sum[4] < ty) ans += ty - sum[3]; else ans += (abs(sum[3] - sum[4] - ty) + 1) / 2; if (abs(sum[1] - sum[2] - tx) % 2 && std::abs(sum[3] - sum[4] - ty) % 2) -- ans; cout << ans << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
C SW的糖果树(困难版本)— 启发式合并优化
思路和简单暴力版一样 只是多了启发式合并
这里大概说一下为什么可以用启发式合并, 因为每个子节点遍历完后就不会再遍历了,如果不进行启发式合并就相当于把子节点对应的子树信息 更新到父节点上,但是可能存在父节点存的信息更少,如果把子节点信息更新到父节点上就会变慢,所以可以进行启发式合并进行优化,复杂度 O ( n l o g n ) O(nlogn) O(nlogn)#include#include #include #include #include using namespace std; const int N = 100010; int n, a[N], res = 0; bool st[N]; vector<int> g[N]; map<int,int> mp[N]; int maxv[N], maxv_col[N], sum[N]; void dfs(int u) { st[u] = true; mp[u][a[u]] ++; maxv[u] = 1; maxv_col[u] = a[u]; sum[u] = a[u]; for(auto v : g[u]) { if(st[v]) continue; dfs(v); // 启发式合并操作 if(mp[u].size() < mp[v].size()) { swap(mp[u], mp[v]); swap(maxv[u], maxv[v]); swap(maxv_col[u], maxv_col[v]); swap(sum[u], sum[v]); } for(auto [x, c] : mp[v]) { if(mp[u][x] == 0) sum[u] ^= x; mp[u][x] += c; if(mp[u][x] > maxv[u]) { maxv[u] = mp[u][x]; maxv_col[u] = x; } else if(mp[u][x] == maxv[u]) maxv_col[u] ^= x; } } res = max(sum[u] ^ maxv_col[u], res); } signed main() { cin >> n; for(int i = 1; i <= n; i ++) cin >> a[i]; for(int i = 1, u, v; i < n; i ++) { cin >> u >> v; g[u].push_back(v); g[v].push_back(u); } dfs(1); cout << res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
D SW的七星光芒剑 — 数学
找到6个点 连接6条线
需要注意的是 每行*之间有 空格
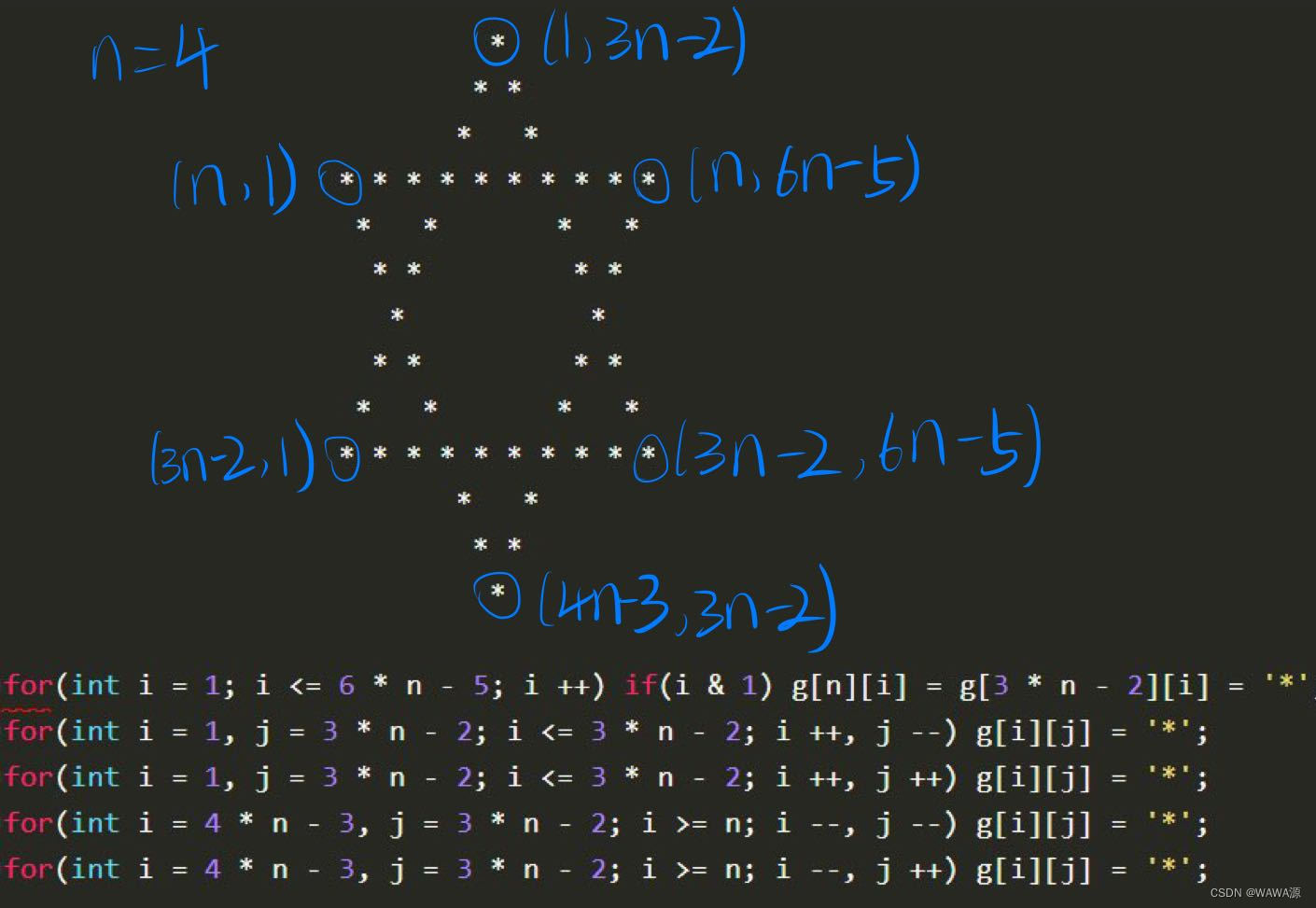
#include#include using namespace std; char g[1010][1010]; signed main() { int n; cin >> n; memset(g, ' ', sizeof g); for(int i = 1; i <= 6 * n - 5; i ++) if(i & 1) g[n][i] = g[3 * n - 2][i] = '*'; for(int i = 1, j = 3 * n - 2; i <= 3 * n - 2; i ++, j --) g[i][j] = '*'; for(int i = 1, j = 3 * n - 2; i <= 3 * n - 2; i ++, j ++) g[i][j] = '*'; for(int i = 4 * n - 3, j = 3 * n - 2; i >= n; i --, j --) g[i][j] = '*'; for(int i = 4 * n - 3, j = 3 * n - 2; i >= n; i --, j ++) g[i][j] = '*'; for(int i = 1; i <= 4 * n - 3; i ++) { for(int j = 1; j <= 6 * n - 5; j ++) cout << g[i][j]; cout << '\n'; } } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
E 井字棋游戏 — 博弈论+ 暴搜
因为要判断a1是否必胜 因此 对于 a1 而言 平局算输,而对于a2而言平局算赢
直接dfs出每种情况 做一个判断,如果存在赢的情况就赢,如果 一种情况都不赢就输
即 有一种必胜就是 必胜 所有必败就是必败#includeusing namespace std; #define int long long int g[10]; // 判断是否获胜 bool win(int x) { for(int i = 0; i < 7; i += 3) if(g[i] == x && g[i + 1] == x && g[i + 2] == x) return true; for(int i = 0; i < 3; i ++) if(g[i] == x && g[i + 3] == x && g[i + 6] == x) return true; if(g[0] == x && g[4] == x && g[8] == x) return true; if(g[2] == x && g[4] == x && g[6] == x) return true; return false; } // 1: 输/平局 0,赢1 // 2: 赢/平局 1, 输0 bool dfs() { int a1 = 0, a2 = 0; for(int i = 0; i < 9; i ++) { a1 += g[i] == 1; a2 += g[i] == 2; } // 最后一步是 p2走的,只要不是p1 赢 p1 就算输 if(a1 + a2 == 9) return !win(1); // 轮到a1 if(a1 == a2) { if(win(1)) return true; if(win(2)) return false; bool f = 0; for(int i = 0; i < 9; i ++) { if(g[i]) continue; g[i] = 1; // 如果存在a2 输了 ,则a1赢 if(dfs() == false) f = 1; g[i] = 0; if(f) return true; } // 如果 a2一直赢 则 a1 必输 return false; } // 先到轮到 a2 与 a1 同理 else { if(win(2)) return true; if(win(1)) return false; bool f = 0; for(int i = 0; i < 9; i ++) { if(g[i]) continue; g[i] = 2; if(dfs() == false) f = 1; g[i] = 0; if(f) return true; } return false; } } signed main() { int a1 = 0, a2 = 0; for(int i = 0; i < 9; i ++) { cin >> g[i]; a1 += g[i] == 1; a2 += g[i] == 2; } int res = dfs(); // 看残局先手是谁, 如果是p2 需要异或一下答案 if(a1 != a2) res ^= 1; cout << (res ? "YES" : "NO") << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
F SW的糖果树(简单版本)— 暴力
这个题意思容易理解错
意思是 求 把一个子树中最大数量的所有颜色去掉 ,求其它颜色的异或和 的 最大值
直接暴力每个子树顶点,然后统计这个子树中最大数量的颜色 再异或去掉#include#include #include using namespace std; #define int long long const int N = 10010; int a[N]; vector<int> g[N]; bool st[N]; map<int,int> mp[N]; int res = 0; void dfs(int u, int fa) { st[u] = true; for(auto v : g[u]) { if(v == fa || st[v]) continue; dfs(v, u); // 把子树中颜色加到父亲节点颜色中 for(auto [x, c] : mp[v]) mp[u][x] += c; } mp[u][a[u]] ++; vector<int> vec; // 统计出现最多的颜色 int maxv = 0, s = 0; for(auto [x, c] : mp[u]) { if(maxv < c) vec.clear(), maxv = c; if(maxv == c) vec.push_back(x); s ^= x; } // 把出现最多的颜色去掉 for(auto x : vec) s ^= x; res = max(res, s); } signed main() { int n; cin >> n; for(int i = 1; i <= n; i ++) cin >> a[i]; for(int i = 1, u, v; i < n; i ++) { cin >> u >> v; g[u].push_back(v); g[v].push_back(u); } dfs(1, -1); cout << res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
G 凑数字 — 构造
n,n-1这两个数不变, 前面全部凑成1,相邻两个相减为1, 然后1 * 1,最后(1 + n - 1) * n
#include#include #include using namespace std; signed main() { int n; cin >> n; if(n == 2) { cout << -1 << '\n'; return 0; } int m = n - 2; vector<string> res; for(int i = m; i > 1; i -= 2) { string s = to_string(i) + " - " + to_string(i - 1); res.push_back(s); } while(res.size() < n - 3) res.push_back("1 * 1"); string s = "1 + " + to_string(n - 1); res.push_back(s); s = to_string(n) + " * " + to_string(n); res.push_back(s); for(auto x : res) cout << x << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
H 旋转数组 — dp
这个一定要读清楚题 连续上升子串 是指 数值连续 1,2,3,4…且位置连续
状态表示:
d p [ i ] [ j ] dp[i][j] dp[i][j]表示 以i列结尾,且数值为j的最长字串长度
状态转移:
d p [ j + 1 ] [ x ] = m a x ( d p [ j + 1 ] [ x ] , d p [ j ] [ x − 1 ] + 1 ) dp[j + 1][x] = max(dp[j + 1][x], dp[j][x - 1] + 1) dp[j+1][x]=max(dp[j+1][x],dp[j][x−1]+1)#include#include #include using namespace std; const int N = 100010; vector<vector<int>> a; map<int,int> dp[N]; int n, m; int res = 0; signed main() { cin >> n >> m; a = vector<vector<int>> (n, vector<int>(m)); for(int i = 0; i < n; i ++) for(int j = 0; j < m; j ++) cin >> a[i][j]; for(int j = 0; j < m; j ++) for(int i = 0; i < n; i ++) { int x = a[i][j]; dp[j + 1][x] = max(dp[j + 1][x], dp[j][x - 1] + 1); res = max(res, dp[j + 1][x]); } cout << res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
I 最小字典序序列 — 小项堆 + 栈 模拟题
这就是个模拟题,开m个栈,记录每个栈 栈顶数值 对应的栈的编号pos
同时维护一个小项堆,每次从小项堆里拿出最小值放入结果中,同时根据pos找到最小值对应的栈的编号,将栈更新#include#include #include #include using namespace std; const int N = 100010; int pos[N]; stack<int> stk[N]; signed main() { int n, m; cin >> n >> m; priority_queue<int, vector<int>, greater<int> > heap; for(int i = 1; i <= m; i ++) { int t, x; cin >> t; while(t --) cin >> x, stk[i].push(x); pos[x] = i; heap.push(x); } string res = ""; while(heap.size()) { int t = heap.top(); heap.pop(); res += " " + to_string(t); if(stk[pos[t]].size()) stk[pos[t]].pop(); if(stk[pos[t]].size()) { int top = stk[pos[t]].top(); heap.push(top); pos[top] = pos[t]; } } cout << res.substr(1) << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
J SW玩扫雷 — 模拟签到
直接模拟,遍历到每个雷,把周围的数值都+1
#include#include using namespace std; char g[110][110]; int res[110][110]; signed main() { memset(res, 0, sizeof res); int n, m; cin >> n >> m; for(int i = 1; i <= n; i ++) cin >> (g[i] + 1); // 设置个负无穷 最后做判断 for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) if(g[i][j] == '*') res[i][j] = -1e9; for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) if(g[i][j] == '*') // 相邻8个数 for(int u = i - 1; u <= i + 1; u ++) for(int v = j - 1; v <= j + 1; v ++) { if(u == i && j == v) continue; res[u][v] ++; } for(int i = 1; i <= n; i ++) { for(int j = 1; j <= m; j ++) if(res[i][j] >= 0) cout << res[i][j]; else cout << "*"; cout << '\n'; } } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
K 亮度 — 暴力
推个数学式子然后暴力, 四维可优化到三维 见代码
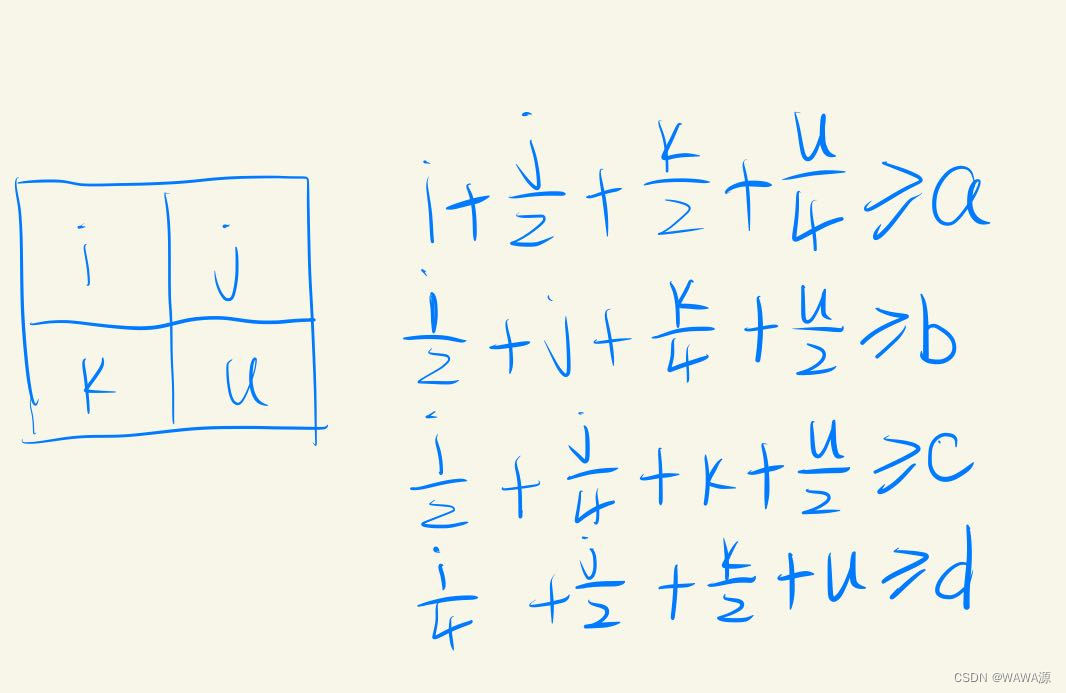
#include#include #include using namespace std; signed main() { int a, b, c, d; cin >> a >> b >> c >> d; int res = 10000; for(int i = 0; i <= 500; i ++) { if(i > res) break; for(int j = 0; j <= 500; j ++) { if(i + j > res) break; for(int k = 0; k <= 500; k ++) { if(i + j + k > res) break; int t1 = (a - (i + j / 2 + k / 2)) * 4; int t2 = (b - (i / 2 + j + k / 4)) * 2; int t3 = (c - (i / 2 + j / 4 + k)) * 2; int t4 = (d - (i / 4 + j / 2 + k / 2)); int u = max({t1, t2, t3, t4}); res = min(res, i + j + k + u); } } } cout << res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
L SW的妙妙区间 — 思维
正难则反的思路 , 我们可以先找不包含0的区间,再用总区间减去
不包含0的区间求解思路
先枚举右端点i,此时右端点固定 找符合条件的左端点数量 加到res中, 离右端点最远的左端点就是到最近的一个包含0的区间,可以用map判断是否包含包含0, map储存前缀和,如果map出现两个相同的值就证明有0出现了,用pos记录最近的0的位置#include#include #include using namespace std; #define int long long const int N = 1000010; int a[N]; signed main() { int n; cin >> n; for(int i = 1; i <= n; i ++) cin >> a[i]; int res = 0; unordered_map<int,int> mp; for(int i = 0, pos = 0, sum = 0; i <= n; i ++) { sum += a[i]; if(mp.count(sum)) pos = max(pos, mp[sum] + 1); mp[sum] = i; res += i - pos; } cout << (n + 1) * n / 2 - res << '\n'; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
-
相关阅读:
联邦学习--记录
论企业数字化和IT组织思考
GBASE 8s 自定义存储过程和函数使用
VSCode操作小技巧
【django framework】ModelSerializer+GenericAPIView,如何在提交前修改某些字段值
HTTP各版本差异
oracle 更新和删除数据
LeetCode 2656.K个元素的最大和
多线程编程
【Lodash】 Filter 与Map 的结合使用
- 原文地址:https://blog.csdn.net/qq_51282224/article/details/127591893
