初阶数据结构 堆（二）

一. 堆的接口函数（续）

虽然我们的上一篇博客已经写过了堆的前面一些接口函数

这里我们再重复一遍

1. 结构体形式

我们这里形式上使用一个数组来表示一个逻辑上的二叉树

// 为了方便复用 我们这里将int重定义下
typedef int HeapType;


// 结构体定义一下
typedef struct Heap
{
	HeapType* arr;
	int size;
	int capacity;
}Hp;

1
2
3
4
5
6
7
8
9
10
11
12

2. 初始化和销毁

这里的两个接口函数都很简单 我们直接连起来动手实现一下

初始化

void HeapInit(Hp* obj)
{
	//assert
	assert(obj);
	// main
	obj->arr = NULL;
	obj->size = 0;
	obj->capacity = 0;
}
1
2
3
4
5
6
7
8
9

销毁

void HeapDestroy(Hp* obj)
{
	// assert
	assert(obj);

	// main
	free(obj->arr);
	obj->arr = NULL;

	obj->size = 0;
	obj->capacity = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12

3. 添加数据（小堆为例）

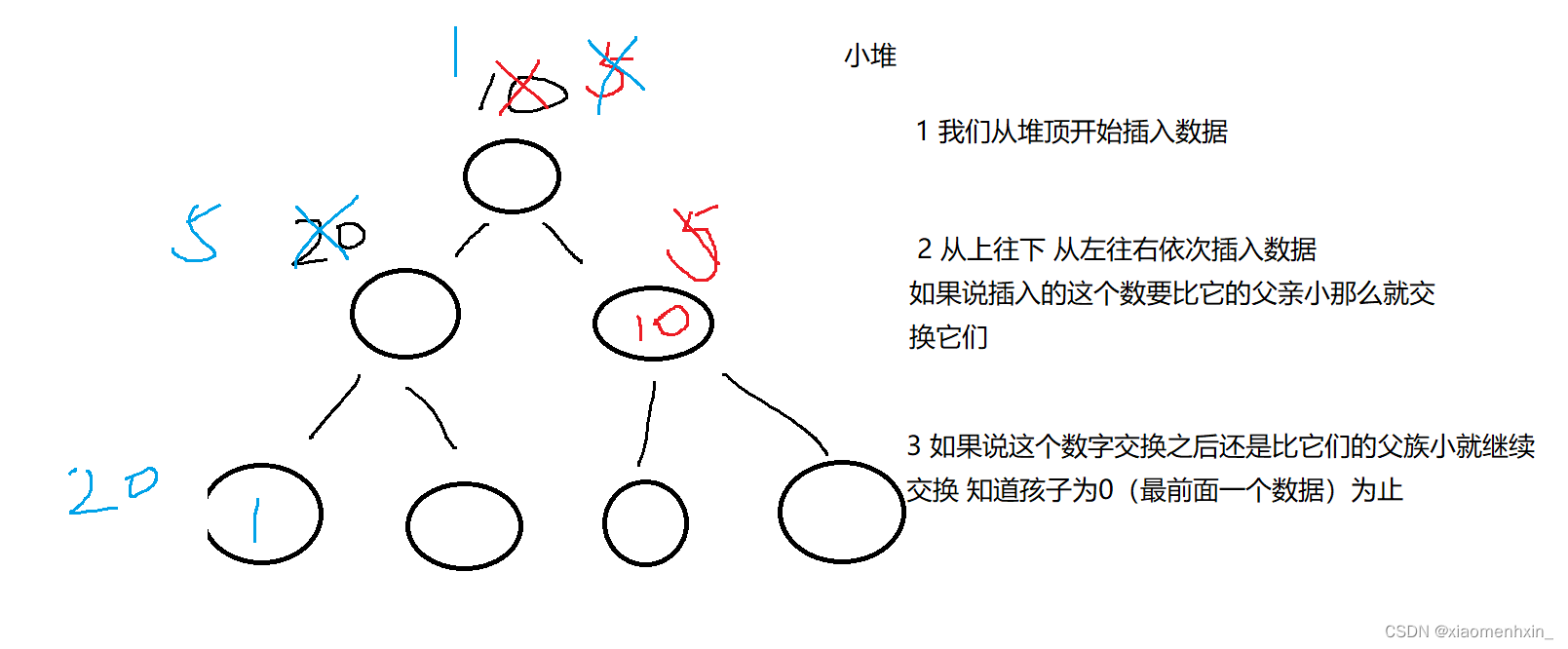
void HeapPush(Hp* obj, HeapType x)
{
	// assert
	assert(obj);
	
	//开辟空间
	if (obj->size==obj->capacity)
	{
		int newcapacity;
		//第一次*2为0
		newcapacity = obj->capacity * 2 + 4;
		//注意这里的sizeof 以及最后的更新capacity
		HeapType* tmp = realloc(obj->arr, sizeof(HeapType) * newcapacity);
		if (tmp=NULL)
		{
			printf("HeapPush realloc error");
			exit(-1);
		}
		else
		{
			obj->arr = tmp;
			obj->capacity = newcapacity;
		}
	}

	//开始插入数据
	obj->arr[obj->size] = x;

	//判断是否需要调整 



}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

这里因为判断是否需要调整这个函数要使用很多次

所以说我们单独写出一个函数出来

void HeapAdjust(Hp* obj, int seat)
{
	// assert
	assert(obj);

	//循环判断孩子是否大于父亲 终止条件是孩子等于0（这个时候孩子就是最前面的位置了）或者不需要调整了
	int child = seat;
	int father = (seat - 1) / 2;
 	while (child)
	{
		// 小堆 上面的最小 所以说如果孩子小就要向上调整
		if (obj->arr[child]<obj->arr[father])
		{
			HeapType tmp;
			tmp = obj->arr[father];
			obj->arr[father] = obj->arr[child];
			obj->arr[child] = tmp;


			//迭代条件
			child = father;
			father = (child - 1) / 2;

		}
		else
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

小堆的调整方式如上

整体代码如下

void HeapPush(Hp* obj, HeapType x)
{
	// assert
	assert(obj);
	
	//开辟空间
	if (obj->size==obj->capacity)
	{
		int newcapacity;
		//第一次*2为0
		newcapacity = obj->capacity * 2 + 4;
		//注意这里的sizeof 以及最后的更新capacity
		HeapType* tmp = realloc(obj->arr, sizeof(HeapType) * newcapacity);
		if (tmp=NULL)
		{
			printf("HeapPush realloc error");
			exit(-1);
		}
		else
		{
			obj->arr = tmp;
			obj->capacity = newcapacity;
		}
	}

	//开始插入数据
	obj->arr[obj->size] = x;
	obj->size++;

	//判断是否需要调整   注意这里不能使用-- 因为这样子使用了就改变size的值了
	HeapAdjust(obj, obj->size - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

4. 打印数据

这个很简单 直接打印数组的顺序就可以

简单来实现一下

void HeapPrint(Hp* obj)
{
	//assert
	assert(obj);


	//按照数组顺序一个个打印数据就可以 
	int i = 0;
	for ( i = 0; i < obj->size; i++)
	{

		printf("%d ", obj->arr[i]);

	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

下面让我们来测试一下

我们发现出现了一个这样子的错误

到底怎么回事呢？

我们debug看看

这里显示obj->arr是一个空指针

难道是我们前面的tmp写错了？

回去一看

果然

HeapType* tmp = realloc(obj->arr, sizeof(HeapType) * newcapacity);
1

忘记强制转换类型了

我们强制转换下类型再试试

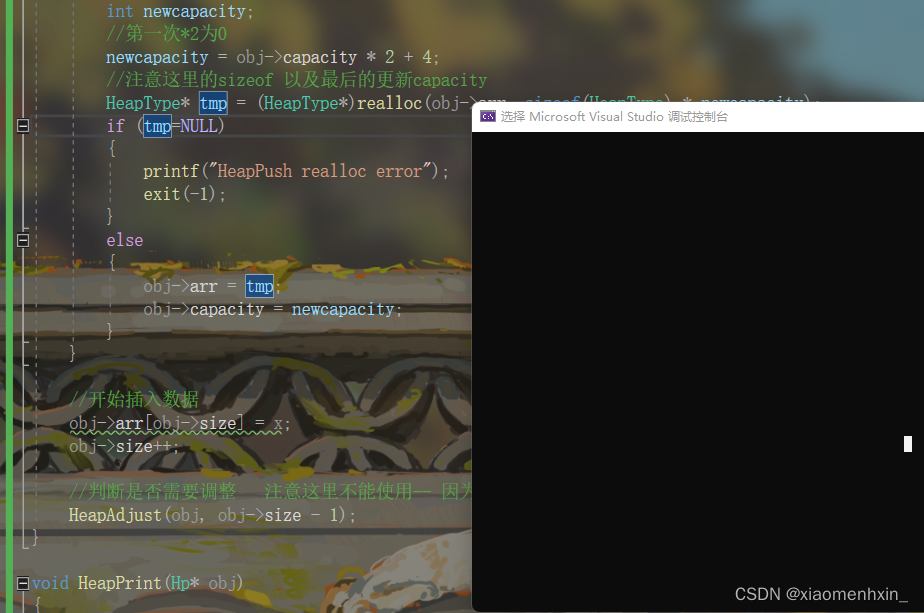
我们发现这里程序还是崩溃了

再debug一下我们就发现了

原来是这一行的条件

if (tmp=NULL)
1

这里要改一下

改成

if (tmp==NULL)
1

这样子就可以啦

我们再来看看效果

5. 删除数据

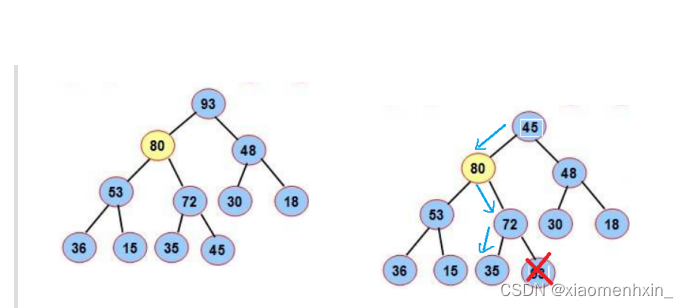
我们想要删除堆中的一个数据 还要不改变这个堆的结构 这个时候怎么办呢

这个时候我们这里给出一种很巧妙的解法

我们先将最前面的元素和最后面的元素交换位置

然后再删除掉堆最后面的元素

之后开始向下调整这个堆

如上图所示

下面是删除数据的大体逻辑

void HeapDelete(Hp* obj)
{
	// assert
	assert(obj);
	assert(obj->arr);
	assert(obj->size > 0);


	// 交换头尾元素
	HeapType tmp = obj->arr[0];
	obj->arr[0] = obj->arr[obj->size - 1];
	obj->arr[obj->size - 1] = tmp;


	//删除尾元素
	obj->size--;


	//向下调整
	


}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

这里我们还需要再写一个函数向下调整

void HeapAdjustDown(Hp* obj,int size)
{
	// assert
	assert(obj);
	
	// set孩子父亲 比较 
	int father = 0;
	int child = 2 * father + 1;

	// 孩子大于等于size的时候结束 
	while (child < size)
	{
		// 右孩子存在 比较两个大小 
		if (child + 1 < size && obj->arr[child + 1] < obj->arr[child])
		{
			child++;
		}
		else
		{
			break;
		}

		//父亲和最大的孩子比较大小 如果大于就交换 如果小于就结束
		if (obj->arr[father] > obj->arr[child])
		{
			HeapType tmp = obj->arr[father];
			obj->arr[father] = obj->arr[child];
			obj->arr[child] = tmp;


			// 交换完迭代
			father = child;
			child = 2 * father + 1;

		}
		else
		{
			break;
		}



	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

调整函数如上

我们再来整体看看这个函数

void HeapDelete(Hp* obj)
{
	// assert
	assert(obj);
	assert(obj->arr);
	assert(obj->size > 0);


	// 交换头尾元素
	HeapType tmp = obj->arr[0];
	obj->arr[0] = obj->arr[obj->size - 1];
	obj->arr[obj->size - 1] = tmp;


	//删除尾元素
	obj->size--;




	//向下调整
	HeapAdjustDown(obj,obj->size);
	


}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

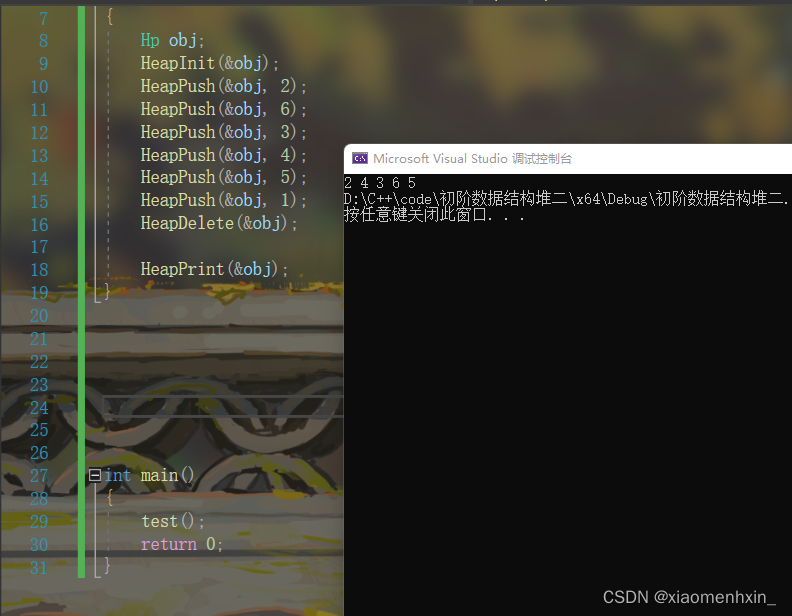
测试一下试试

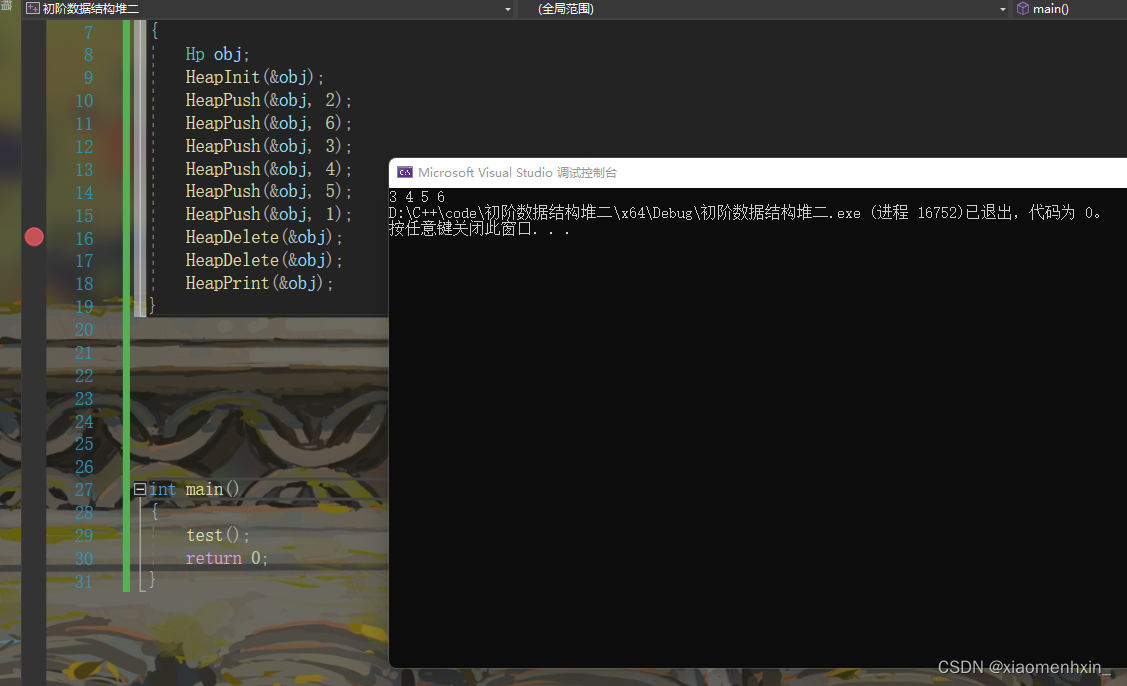
6. 返回大小

这个很简单 返回size大小

int HeapSize(Hp* obj)
{
	return obj->size;
}
1
2
3
4

7. 判断为空

bool HeapEmpty(Hp* obj)
{
	return obj->size == 0;
}
1
2
3
4

以上就是本篇博客的全部内容啦 由于博主才疏学浅 所以难免会出现纰漏 希望大佬们看到错误之后能够

不吝赐教 在评论区或者私信指正 博主一定及时修正

那么大家下期再见咯