TL-BERT: A Novel Biomedical Relation Extraction Approach

论文地址：TL-BERT: A Novel Biomedical Relation Extraction Approach

1. Introduction

在句子级别提取生物医学关系时，那些同源但不同类（SODC）的实例很容易被错误地划分为同一类。

示例句子包含三个蛋白质实体 TPO、Grb2 和 JAK2，它们可以形成三种候选关系。其中，实例 和实例 是 SODC 实例。由于 SODC 实例是从同一个句子生成的，它们具有几乎相同的词汇信息和句法信息，这会误导分类器将它们划分为同一类。

受 FaceNet 中三重损失策略的启发，我们提出了基于三重损失的 BERT（TL-BERT）模型来从文本中提取 DDI 和 PPI。我们试图最大化这些由相同句子生成但属于不同类的实例之间的距离，以增加 SODC 实例之间的区别。首先，使用指定的三重生成规则生成三重数据。其次，将生成的三重数据输入到基于 BERT 的特征抽取器中以获取句子级特征和实体级特征。最后，基于句子级和实体级特征，分别计算三重损失和二元交叉熵损失来训练模型。TL-BERT 分别在 PPI 数据集和 DDI 数据集上进行了评估，并取得了显著的结果。此外，引入三重损失训练策略可以提高 PPI 提取任务和 DDI 检测任务的性能，这证明了三重损失训练策略在关系提取领域的有效性。

2. Method

在本研究中，我们着重于巧妙地使用三重损失训练策略来训练基于 BERT 的生物医学关系提取模型。我们的方法框架如图所示：

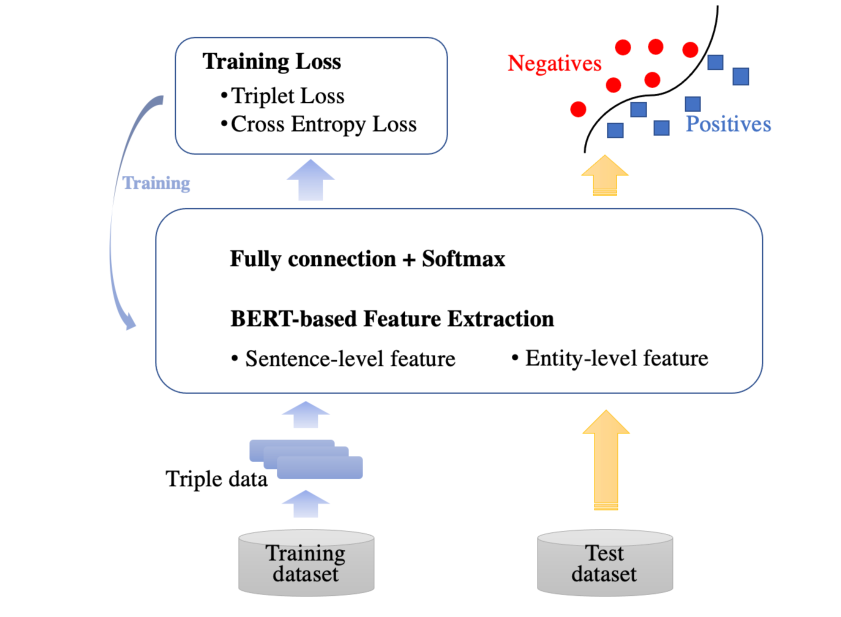
2.1 Triple Data Generation

为了配合 Triplet Loss 的训练策略，将使用以下三条规则生成合法的三重数据：
（1）对于每个正实例，从同一个句子中获取一个负实例，从随机选择的句子中获取一个正实例，以形成三重数据。
（2）对于每个负实例，从同一个句子中获取一个正实例，从随机选择的句子中获取一个负实例，以形成三重数据。
（3）对于每个无法从同一个句子中找到一个负/正实例的正/负实例，若该句子中只有两个实体，那么它将从其它句子中随机选择一个正实例和一个负实例，以形成三重数据。
对于使用规则（1）和规则（2）生成的三重数据，三重数据中的两个实例共享相同的上下文信息，这将误导分类器将它们分到同一类中，引入 Triplet Loss 策略的主要目的是提高区分这些 SODC 实例的能力。

2.2 Bert based feature extraction

R-BERT 将实体级信息合并到预训练的BERT模型中用于关系分类，并达到了最先进的水平。因此，我们使用R-BERT作为特征抽取器，从输入实例中提取句子级特征和实体级特征。在输入到特征提取器之前需要处理每个实例。给定具有两个实体 $e1$ 和 $e2$ 的句子，我们需要在实体 $e1$ 的开头和结尾插入 $，在实体 $e2$ 的开头和结尾插入 #。

经过预处理后，实例被送入基于 BERT 的特征提取器。首先，BERT 模型将处理后的实例（标记序列）映射到隐藏状态序列 H = { H 0 , H 1 , ⋯   , H N } H=\{H_0,H_1,\cdots,H_N\} H={H0​,H1​,⋯,HN​}。$H_0$ 是第一个 token [CLS]（被视为句子级别的嵌入）的嵌入，$H_i\sim H_j$ 是实体 $e1$ 的嵌入，$H_m\sim H_n$ 是实体 $e2$ 的嵌入。由于每个实体的长度不一致，因此我们用平均操作来获得具有指定长度的实体级嵌入。此外，为了提取更多的抽象特征，在句子级嵌入和实体级嵌入中都添加了一个全连接层，以获得最终的句子级特征向量 $H_S$ 和实体级特征向量$H_{e1}$ 和$H_{e2}$，分别表示为：$$H_S=W_0[\text{tanh}(H_0)]+b_0\text{\hspace{1em}(1)}$$$$H_{e1}=W[\text{tanh}(\frac{1}{j-i+1}\sum _{t=i}^j{H}_t)]+b\text{\hspace{1em}(2)}$$$$H_{e2}=W[\text{tanh}(\frac{1}{m-n+1}\sum _{t=m}^n{H}_t)]+b\text{\hspace{1em}(3)}$$

2.3 Training process

Triplet Loss培训策略的设计动机如图所示。在特征空间中，我们希望最大化 SODC 实例（Instance1 和 Instance3）之间的距离，并最小化这些相同类实例（Instance1 和 Instance2）之间的间距。通过对每个实例嵌入新的特征，分类器可以更准确地区分 SODC 实例。

TL-BERT 的总体训练过程如图所示：

---

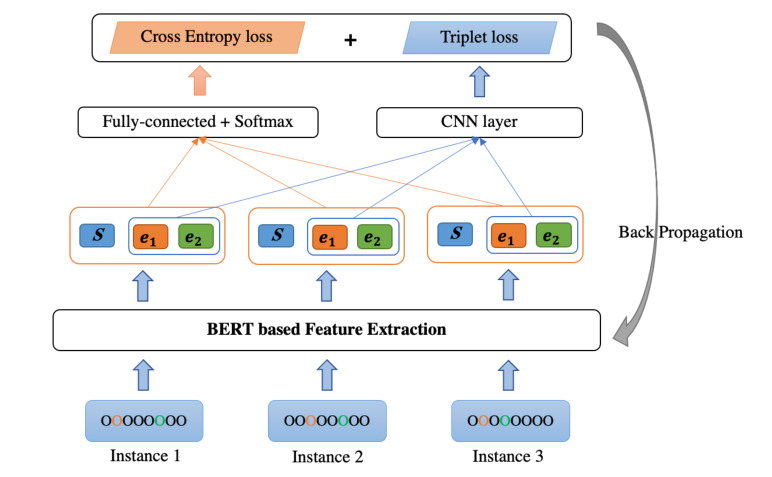
（1）交叉熵损失
对于三重数据中的每个实例，将句子级特征向量 $H_0^{’}$ 和两个实体级特征向量 $H_{e1},H_{e2}$ 拼接起来，然后添加一个全连接层和一个 $\text{softmax}$ 层以获得最终分类结果 $p$。最终使用公式（6）计算交叉熵损失，其中 $i=1,2,3$ 分别代表三重数据实体1、实体2和实体3的索引。$$e=W_3[concat(H_S;H_{e1};H_{e2})]+b_3\text{\hspace{1em}(4)}$$$$p=\text{softmax}(e)\text{\hspace{1em}(5)}$$$$los{s}_{CE}=\sum _{i=1}^3-[y^i\cdot \log (p^i)+(1-y^i)\cdot \log (1-p^i)]\text{\hspace{1em}(6)}$$

（2）三重损失
对于 SODC 实例，它们共享相同的上下文信息，唯一的区别是实体级别的信息。因此，我们推断实体级别的信息对将这些 SODC 实例正确分类起着关键作用。因此，我们基于实体级特征向量计算三重损失。
首先，对于每个实例，将两个实体级特征向量 $H_{e1}\in R^d，H_{e2}\in R^d$ 堆叠获得向量 $H_e\in R^{2\times d}$。然后，为捕获实体对的相关信息，在 $H_e$ 上执行一维卷积，使用公式（8）获得实体对卷积特征向量 $H_{ep}\in R^d$。最后，使用三个实体级卷积特征向量来计算三重损失。$$H_e=stack[H_{e1},H_{e2}]\text{\hspace{1em}(7)}$$$$H_{ep}=f_{conv}(H_e)\text{\hspace{1em}(8)}$$$$los{s}_{TL}=[||H_{ep}^1-H_{ep}^2|{|}_2^2-||H_{ep}^1-H_{ep}^3|{|}_2^2+\alpha {]}_{+}\text{\hspace{1em}(9)}$$其中，$H_{ep}^1，H_{ep}^2，H_{ep}^3$分别代表实体1、实体2、实体3的实体对卷积特征向量。实体1和实体2属于同一个类，而实体1与实体3属于不同的类。$\alpha$不同类之间强加的边距。

---

综上，TL-BERT 的损失函数定义如下，$\beta$ 是超参数：$$loss=los{s}_{CE}+\beta los{s}_{TL}\text{\hspace{1em}(10)}$$

3. Experiments

在本章中，我们将验证 TL-BERT 在 PPI 提取任务和 DDI 检测任务中的有效性。

3.1 Datasets

我们的方法是根据两个流行的 PPI 基准（AIMed、BioInfer）和一个著名的 DDI 基准（DDI Extraction-2013语料库）进行评估的。基于 DDI Extraction-2013 有两个子任务：DDI 检测（二进制分类）和 DDI 分类（多分类）。由于三重损失不适用于多类分类任务，因此我们只进行 DDI 检测任务来验证我们的训练策略的有效性。

3.2 Experimental Results and Analysis

为了验证 TL-BERT 的有效性，进行了以下实验。由于 AIMed 和 BioInfer 中没有测试数据集，因此对这两个语料库进行了十次交叉验证实验。PPIs 语料库和 DDIs 语料的比较结果分别如表I和表II所示。