• 14天机器学习DAY1-5｜线性回归原理小结

    14天阅读挑战赛
    努力是为了不平庸~
    线性回归是机器学习中最基本的问题类型，熟练掌握线性回归问题也是为以后掌握机器学习打下坚实基础!

    目录

    1.线性回归的模型函数和损失函数

    2.线性回归的算法

    3.线性回归的推广：多项式回归 

    4.线性回归的推广：广义线性回归​​​​​​​

    5.线性回归的正则化

    1.线性回归的模型函数和损失函数

            线性回归遇到的问题一般是这样的。我们有m个样本，每个样本对应于n维特征和一个结果输出，如下：(x_{1}^{(0)},x_{2}^{(0)},... x_{n}^{(0)},y_{0}),(x_{1}^{(1)},x_{2}^{(1)},... x_{n}^{(1)},y_{1}),...(x_{1}^{(m)},x_{2}^{(m)},... x_{n}^{(m)},y_{m})

            我们的问题是，对于一个新的(x_{1}^{(x)},x_{2}^{(x)},... x_{n}^{(x)},y_{x})，他所对应的y_{x}是多少？如果这个问题里面的y是连续的，则是一个回归问题，否则是一个分类问题。

            对于n维特征的样本数据，如果我们决定使用线性回归，那么对应的模型是这样的：

            h_{\theta }(x_{1},x_{2},...x_{n})=\theta _{0}+\theta _{1}x _{1}+\cdot \cdot \cdot +\theta _{n}x_{n},其中\theta _{i}（i=0,1,2...n）为模型参数，x_{i}（i=0,1,2...n）为每个样本的n个特征值。这个表示可以简化，我们增加一个特征x_{0}=1，这样h_{\theta }(x_{1},x_{2},...x_{n})=\sum_{i=0}^{n}\theta _{i}x_{i}

            进一步用更加简洁的矩阵形式表达：h_{\theta }(X)=X\theta，​​​​​​​其中，假设函数h_{\theta }(X)为m*1的向量，\theta为n*1的向量，里面有n个代数法的模型参数。X为m*n维的矩阵，m代表样本的个数，n代表样本的特征数。

            得到模型之后，我们需要求出损失函数，一般线性回归中，我们用均方误差作为损失函数，先写出损失函数的代数表示形式，然后再写出矩阵形式 。由于矩阵表达简洁，后面我们将统一采用矩阵方式表达模型函数和损失函数。

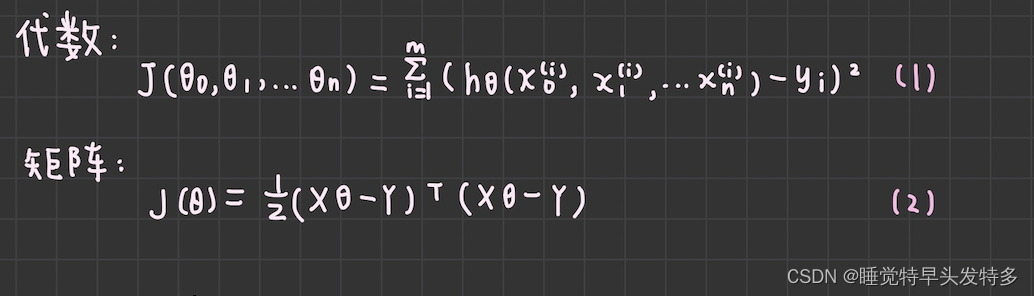
    2.线性回归的算法

            对于线性回归的损失函数式(2)，我们常用两种方法来求损失函数最小化时的\theta参数：第一种是梯度下降法，第二种是最小二乘法，公式如下；当然线性回归还有其他的常用算法，如牛顿法和拟牛顿法。

      

    "递"改"梯"

    3.线性回归的推广：多项式回归 

            回到最开始的线性模型h_{\theta }(x_{1},x_{2},...x_{n})=\theta _{0}+\theta _{1}x _{1}+\cdot \cdot \cdot +\theta _{n}x_{n}，如果这里不仅仅是x的一次方，比如扩大至二次方，那么模型就变成了多项式回归。我们写出只有两个特征的二次方多项式回归的模型：

             可以发现，我们又重新回到了线性回归，这是一个五元线性回归，可以用线性回归的方法来完成算法。对于每个二元样本特征(x_{1},x_{2}),我们得到一个五元样本特征：(1,x_{1},x_{2},x_{1}^{2},x_{2}^{2},x_{1}x_{2}),通过这个改进后的五元样本特征，我们重新把不是线性回归的函数又变为线性回归的函数。

     

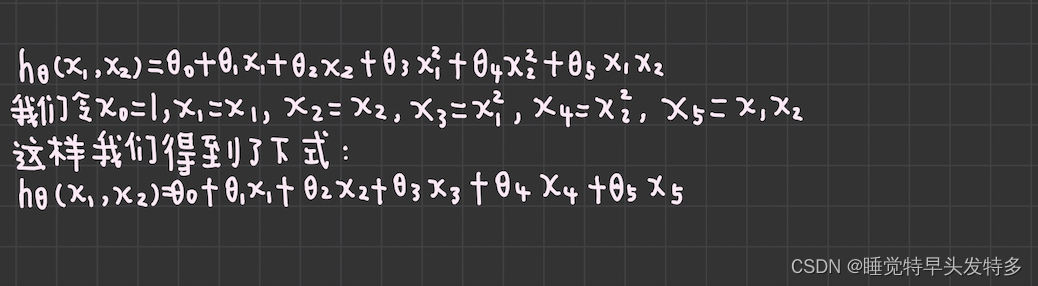
    4.线性回归的推广：广义线性回归

            在上一节的线性回归的推广中，我们对样本特征x做了推广，这里我们对于特征y做推广。比如我们输出Y不满足和X的线性关系，但是lnY和X满足线性关系，模型函数如下：

    lnY=X\theta；

            这样对于每个样本的输入y，我们用lny去对应，从而仍然可以用线性回归的算法去处理这个问题。我们把lnY一般化，假设这个函数是单调可微函数g(\cdot ),则一般化的广义线性回归形式是：g(Y)=X\theta 或者 Y=g^{-1}(X\theta ),这个函数g(\cdot )我们通常称为联系函数。

    5.线性回归的正则化

            为了防止模型的过拟合，我们建立线性模型的时候经常需要加入正则化项。一般有L1正则化和L2正则化。

            线性回归的L1正则化通常称为Lasso回归，它和一般线性回归的区别是在损失函数上增加了一个L1正则化的项，L1正则化的项有一个常数系数\alpha来调节损失函数的均方差和正则化项的权重，具体Lasso回归的损失函数表达式如下：

            Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。

            Lasso回归的求解办法一般有坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression），由于它们比较复杂，我会单独一篇讲述!

       

     下标的1放到外面 

            线性回归的L2正则化通常称为Ridge回归，它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项，和Lasso回归的区别是Ridge回归的正则化项是L2的范数，而Lasso回归的正则化项是L1的范数，具体Ridge回归的损失函数表达式如下：

             Ridge回归在不抛弃任何一个特征的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但和Lasso回归比，这会使得模型的特征保留的特别多，模型解释性差。

            Ridge回归的求解比较简单，一般用最小二乘法。这里给出用最小二乘法的矩阵推导形式，和普通线性回归类似。

            范数(norm)是数学中的一种基本概念。在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量向量空间（或矩阵）中某个向量的长度或大小。 

            除了上面两种常见的线性回归正则化，还有一些其他的线性回归正则化算法，区别主要在于正则化项和损失函数的优化方式的不同~ 

  • 相关阅读:
    写给前端程序员的命令行入门
    消失的它：网络层分片包中的第一个分片包去哪了？
    python---25---取出指定时间段的日志并写入文件中
    Java注解(Annotation)与元注解
    云原生架构如何助力大数据和AI技术在软件开发中的深度整合
    Elasticsearch
    外包公司“混”了2年，我只认真做了5件事，如今顺利拿到阿里 Offer。
    Spring Cloud 综述
    Qt http get请求数据阻塞和非阻塞实现源码
    我的第一个项目(三)：注册登陆功能(后端)
  • 原文地址：https://blog.csdn.net/m0_57656758/article/details/127411164